Метод проб и ошибок
Сущность метода
Суть метода следует из его названия и состоит в следующем: строится теоретическая модель (т.е. задаются координаты 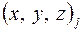 атомов ячейки), по которым рассчитываются структурные амплитуды, или, чаще, структурные факторы. Расчетные значения
атомов ячейки), по которым рассчитываются структурные амплитуды, или, чаще, структурные факторы. Расчетные значения 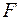 или
или 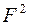 сравнивают с соответствующими экспериментальными значениями. При их совпадении теоретическая структурная модель считается соответствующей структуре кристалла. В противном случае теоретическая модель отвергается и строится новая.
сравнивают с соответствующими экспериментальными значениями. При их совпадении теоретическая структурная модель считается соответствующей структуре кристалла. В противном случае теоретическая модель отвергается и строится новая.
При построении моделей многое зависит от опыта и изобретательности экспериментатора, от учета ряда кристаллофизических и кристаллохимических представлений и фактов.
Вообще говоря, для детального описания метода проб и ошибок необходимо привести полный курс кристаллохимии в достаточно большом объеме (например, Бокий «Кристаллохимия»).
Рассмотрим наиболее важные положения, которые необходимо обязательно учитывать при построении структурных моделей.
Принципы плотнейшей упаковки
Атомы моделируются шарами и укладываются таким образом, чтобы коэффициент компактности 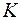 - отношение занятого шарами объема ко всему объему объекта - был наибольшим:
- отношение занятого шарами объема ко всему объему объекта - был наибольшим:
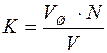 ,
,
где 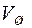 - объем шара;
- объем шара;
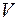 - объем объекта;
- объем объекта;
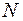 - число шаров.
- число шаров.
Существуют плотнейшие упаковки двух типов:
1. Гексагональная плотнейшая упаковка, которая возникает в том случае, когда слои атомов чередуются по закону АВАВАВ… (шары третьего слоя уложены точно над шарами первого слоя)
2. Кубическая плотнейшая упаковка соответствует порядку чередования слоев АВСАВС… При этом третий слой атомов укладывается над пустотой первого слоя.
Для ионных кристаллов принцип плотнейшей упаковки используется с наивысшей эффективностью. Значительную помощь в построении структурных моделей кристаллов с ионным типом связи оказывают правила, предложенные Полингом, учитывающие соотношения размеров атомов и характер их расположения и взаимодействия в структуре.
Правило первое
Каждый атом окружен полиэдром из анионов. Расстояние катион-анион определяется суммой, а координационное число – отношением ионных радиусов.
Для построения структуры необходимо сначала создать плотнейшую упаковку из анионов. Затем катионы размещаются по пустотам анионной упаковки. В анионной упаковке могут быть пустоты различного типа.
На рисунке а изображена пустота между атомами, лежащими в одной плоскости. На рисунке б атомы (шары) лежащие над плоскостью чертежа изображены заштрихованными окружностями. Совершенно ясно, что размеры пустоты между атомами на рис. а меньше, чем на рис.б, а. эта пустота, в свою очередь, меньше, чем на рис. в.
Если катион достаточно мал, то он может войти в пустоту типа а. Координационное число для этого случая равно 3. Если отношение радиуса катиона ( 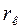 ) к радиусу аниона (
) к радиусу аниона ( 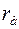 ) равно 0,22, то катион войдет в тетраэдрическую пустоту (рис. б). Пустота названа тетраэдрической потому, что если соединить центры анионов прямыми линиями, то получится тетраэдр. Аналогичное построение для анионов упаковки (рис. в) позволяет получить октаэдр.
) равно 0,22, то катион войдет в тетраэдрическую пустоту (рис. б). Пустота названа тетраэдрической потому, что если соединить центры анионов прямыми линиями, то получится тетраэдр. Аналогичное построение для анионов упаковки (рис. в) позволяет получить октаэдр.
Для тетраэдров координационное число равно 4, для октаэдров – 6.
Координационное число связано с отношением радиусов катионов к радиусам анионов. В таблице представлены значения координационных чисел для различных отношений катионных радиусов к анионным.
Таблица
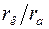
| 0,15 | 0,22 | 0,41 | 0,73 | 1,0 | |
| К. ч. |
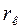 ,
, 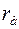 - радиусы катионов и анионов соответственно; к.ч. – координационное число.
- радиусы катионов и анионов соответственно; к.ч. – координационное число.
Правило второе
Структура должна быть электронейтральной. Все положительные катионные заряды должны компенсироваться отрицательными зарядами ближайших анионов. Элементарная ячейка не может нести электрического заряда.
Правило третье.
Наиболее устойчивая структура будет в том случае, если структурные полиэдры, т. е. многогранники, созданные центрами анионов, имеют наименьшее число общих элементов.
Если полиэдры сочленяются вершинами, структура самая устойчивая. Если общими являются грани, то структура наименее устойчива.
Правило четвертое
Если в кристалле есть катионы нескольких сортов, то катионы с большей валентностью и меньшим координационным числом располагаются так, чтобы окружающие их анионные полиэдры не имели общих элементов.
Правило пятое
Число кристаллохимически различных единиц в кристалле должно быть наименьшим, т.е. каждый катион занимает в структуре вполне определенное положение.
Принципы плотнейшей упаковки с большей эффективностью могут быть использованы не только для ионных кристаллов. В этом случае необходимо атомы представлять не шарами, а другими геометрическими телами.
Учет симметрии кристаллов при построении структурной модели
При решении задач второго этапа структурного анализа характеристики симметрии кристалла должны быть известными, так же как известны параметры элементарной ячейки и индексы отражений. Зная параметры элементарной ячейки, можно определить ее объем 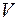 , а по данным химического анализа найти формульную единицу (Ф.Е.). Пусть ее масса есть
, а по данным химического анализа найти формульную единицу (Ф.Е.). Пусть ее масса есть 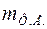 , тогда число формульных единиц, приходящихся на ячейку, определится по формуле
, тогда число формульных единиц, приходящихся на ячейку, определится по формуле
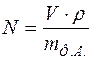 ,
,
где 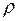 - плотность вещества.
- плотность вещества.
Зная число формульных единиц, приходящихся на одну ячейку, и весь набор элементов симметрии, можно найти некоторые координаты отдельных атомов. Для того, чтобы подробно описать этот вопрос, необходимо рассмотреть понятие правильной системы точек, которое связано с понятием Федоровской группы. В качестве примера рассмотрим Федоровскую группу 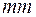 , в которой есть две взаимно перпендикулярные плоскости отражения, а линия их пересечения является осью второго порядка. Графически эта группа изображена на рисунке.
, в которой есть две взаимно перпендикулярные плоскости отражения, а линия их пересечения является осью второго порядка. Графически эта группа изображена на рисунке.
 |
Группа
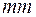 означает существование плоскостей 1 и 2, но так как рассматривается кристалл, то на определенном расстоянии по Х и по У (на трансляции, равной параметру элементарной ячейки) появятся плоскости
означает существование плоскостей 1 и 2, но так как рассматривается кристалл, то на определенном расстоянии по Х и по У (на трансляции, равной параметру элементарной ячейки) появятся плоскости 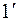 и
и 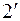 тождественные соответственно 1 и 2 ,так как в кристалле при перемещении на трансляцию «все должно повторяться», т.е. существование плоскости 1 вызывает появление плоскости
тождественные соответственно 1 и 2 ,так как в кристалле при перемещении на трансляцию «все должно повторяться», т.е. существование плоскости 1 вызывает появление плоскости 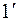 , а 2 →
, а 2 → 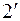 .В таком случае необходимо рассматривать взаимодействие плоскости отражения и трансляции, приводящее к возникновению плоскости отражения на середине трансляции (
.В таком случае необходимо рассматривать взаимодействие плоскости отражения и трансляции, приводящее к возникновению плоскости отражения на середине трансляции ( 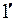 и
и 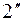 ).Пусть начало координат расположено в точке О.Направление осей координат на рисунке показано. Любое положение точек в пределах этой «элементарной ячейки симметрии»строго описывается набором координат. Точка, обозначающая центр атома, может находиться не на элементе симметрии (допустим в точке А). Пусть ее координаты есть (ху). Но в таком случае появится точка
).Пусть начало координат расположено в точке О.Направление осей координат на рисунке показано. Любое положение точек в пределах этой «элементарной ячейки симметрии»строго описывается набором координат. Точка, обозначающая центр атома, может находиться не на элементе симметрии (допустим в точке А). Пусть ее координаты есть (ху). Но в таком случае появится точка 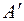 (правильнее А , так как
(правильнее А , так как 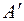 абсолютно тождественна точке А, штрихи проставлены только для удобства) с координатами
абсолютно тождественна точке А, штрихи проставлены только для удобства) с координатами 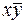 .
.
Но кроме 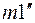 есть
есть 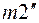 и
и 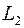 , это приведет к появлению точек
, это приведет к появлению точек 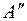 и
и 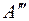 , абсолютно тождественных точке
, абсолютно тождественных точке 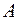 . Набор координат симметрично-тождественных точек определяет правильную систему точек группы. В данном случае это общая правильная система точек, так как
. Набор координат симметрично-тождественных точек определяет правильную систему точек группы. В данном случае это общая правильная система точек, так как 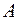 не лежит на элементе симметрии, т.е. находится в общем положении.
не лежит на элементе симметрии, т.е. находится в общем положении.
Если бы точка 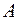 лежала на элементе симметрии, то возникла бы частная правильная система точек. Например, если
лежала на элементе симметрии, то возникла бы частная правильная система точек. Например, если 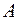 лежит на
лежит на 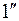 , то частная правильная система точек определится
, то частная правильная система точек определится 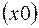 и
и 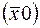 , если
, если 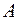 лежит на
лежит на 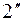 →
→ 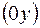 и
и 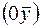 . Если же
. Если же 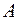 лежит на оси второго порядка, то частная правильная система точек есть
лежит на оси второго порядка, то частная правильная система точек есть 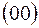 .
.
Предположим, что химическая формула исследуемого вещества записывается 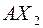 . Допустим, что на элементарную ячейку приходится одна молекула. Тогда, не проводя еще анализа, можно предположить две структурные модели с координатами:
. Допустим, что на элементарную ячейку приходится одна молекула. Тогда, не проводя еще анализа, можно предположить две структурные модели с координатами:
1. 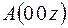
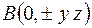 ;
;
2. 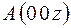
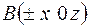 .
.
Если бы не учли Федоровскую группу, то надо было бы определять девять координат 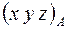 ,
, 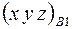 ,
, 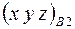 . С учетом группы требуется определить только три координаты для каждой модели.
. С учетом группы требуется определить только три координаты для каждой модели.
Аналогичным образом можно анализировать модели любой Федоровской группы. Частные и общие правильные системы точек для всех Федоровских групп сведены в специальные таблицы. Надо только научиться пользоваться ими, и при достаточной практике самостоятельно вывести правильные системы точек совсем не сложно.
Каждая правильная система точек характеризуется строго определенным числом тождественных точек, кратностью, что очень помогает при построении структурных моделей.
Знание Федоровской группы помогает строить структурные модели еще и потому, что существование тех или иных элементов симметрии налагает определенные ограничения на область возможных расположений центров атомов.
Предположим, что в кристалле группы 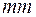 в общем положении необходимо разместить атом с радиусом
в общем положении необходимо разместить атом с радиусом 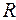 . Центр атома не может находиться на расстоянии от плоскости отражения меньшем, чем
. Центр атома не может находиться на расстоянии от плоскости отражения меньшем, чем 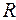 (ибо тогда межатомное расстояние между ним и его зеркальным аналогом было бы меньше
(ибо тогда межатомное расстояние между ним и его зеркальным аналогом было бы меньше 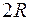 , что невозможно), т.е.появляются области, запрещенные для расположения атомов (на рисунке они заштрихованы). Учитывая, что во многих структурах выполняется принцип плотнейшей упаковки, можно ожидать, что разрешенные области будут иметь достаточно малый объем по сравнению с объемом всей ячейки.
, что невозможно), т.е.появляются области, запрещенные для расположения атомов (на рисунке они заштрихованы). Учитывая, что во многих структурах выполняется принцип плотнейшей упаковки, можно ожидать, что разрешенные области будут иметь достаточно малый объем по сравнению с объемом всей ячейки.

Использование физических свойств кристалла при построении моделей
При построении структурной модели необходимо руководствоваться не только свойствами симметрии решетки, но и физическими свойствами характеристиками кристалла. Структура кристаллов является той основой, которая определяет все его свойства. От физических характеристик объекта перейти к его структуре не всегда представляется возможным, т.к. различные дефекты структуры могут оказать очень сильное влияние на его свойства. Кроме того свойства кристаллов зависят еще от природы атомов в структуре. И все же отдельные рекомендации такого перехода в настоящее время разработаны.
Прежде всего, необходимо учитывать связь между структурной и внешней формой (габитусом) кристалла. Кристалл всегда огранен такими плоскостями, энергия связи между атомами по которым является наибольшей. Например, если молекулы линейной формы располагаются параллельно друг другу, то скорость роста будет наибольшей в направлении перпендикулярном удлиненной молекуле, что и определит наиболее развитую грань. Плоские молекулы, располагаясь параллельно друг другу, создают кристаллы игольчатого габитуса. Если линейные или плоские молекулы не параллельны друг другу в структуре, то кристалл будет развиваться равномерно по всем направлениям.
Зная оптические свойства (показатели преломления для трех направлений и инфракрасные спектры) можно решить вопрос об ориентации отдельных атомных комплексов в структуре.
Существенным дополнением к выводам из структурного анализа могут служить сейчас хорошо известные связи между структурой и свойствами. Например, пьезоэффекты наблюдаются только в кристаллах, не имеющих центра симметрии. Если в кристалле отсутствует плоскость симметрии, то он обнаруживает явление круговой поляризации. Поляризация второго рода является достаточно надежным критерием того, что в кристалле есть инверсионные оси.
Существование кристаллов с одинаковым типом структуры (изотопы) также может помочь в построении структурной модели. В этом случае необходимо только правильно выбрать изотоп.
Выбор модели
Метод проб и ошибок по своей сути предполагает существование нескольких моделей, которые с примерно одинаковой вероятностью претендуют на роль искомой. Окончательный выбор должен быть сделан на основе анализа рентгеноструктурных исследований. В идеальном случае та модель соответствует структуре кристалла, которая имеет значения структурных амплитуд, равные экспериментальным, те. вычисленные по модели
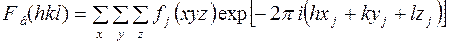 (1)
(1)
должны равняться экспериментальным значениям 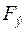 . Но на практике всегда получается расхождение между ними. В качестве характеристики совпадения модели со структурой принимают величину
. Но на практике всегда получается расхождение между ними. В качестве характеристики совпадения модели со структурой принимают величину
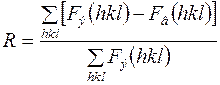 , (2)
, (2)
где 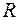 - величина, называемая фактором достоверности.
- величина, называемая фактором достоверности.
Из всех структурных моделей искомой соответствует та, для которой 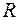 имеет наименьшее значение.
имеет наименьшее значение.
Так как значения 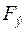 найти довольно трудно (фазовая проблема должна быть решена), то при расчете фактора достоверности можно использовать модуль
найти довольно трудно (фазовая проблема должна быть решена), то при расчете фактора достоверности можно использовать модуль 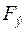 , либо
, либо 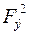 , т.е. расчет должен выполняться по формулам (3), (4):
, т.е. расчет должен выполняться по формулам (3), (4):
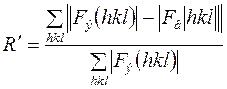 , (3)
, (3)
,
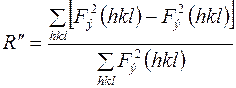 . (4)
. (4)
Различные 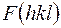 могут определяться с неодинаковыми погрешностями, поэтому в формулах (2-4) часто вводятся «весовые коэффициенты»
могут определяться с неодинаковыми погрешностями, поэтому в формулах (2-4) часто вводятся «весовые коэффициенты» 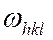 , причем
, причем
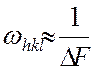 . (5)
. (5)
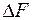 - ошибка измерения структурной амплитуды.
- ошибка измерения структурной амплитуды.
С учетом (5) формула расчета фактора достоверности (например, аналогичная формуле (2))будет:
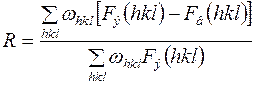 . (6)
. (6)
Метод проб и ошибок исторически является первым методом структурного анализа, но до сих пор он широко применяется в практике исследования структур. Например, главным образом на основе этого метода была раскрыта структура молекулы дезоксирибонуклеиновой кислоты (молекулы ДНК).
Дата добавления: 2015-08-20; просмотров: 858;
