Преобразование формул при наличии элементов симметрии

Наличие элементов симметрии не только сокращает количество членов суммы ряда

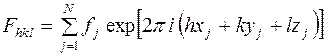. (1)

В тригонометрической форме, выделив действительную и мнимую части, формулу (1) можно записать:

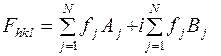, (2)

где , .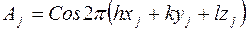

Рассмотрим несколько случаев.

1. Структура центросимметричная.

При наличии в структуре центра инверсии начало координат удобно совмещать с центром инверсии. В этом случае в формуле (2) останется только вещественная часть – косинусные члены суммы:

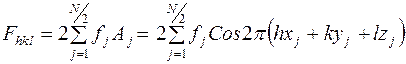. (3)

Возможны только два варианта начальной фазы для любого дифрагированного луча: 0 или 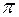. Соответственно величина 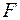может принимать два варианта значений:

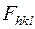>0 при 0

и 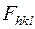<0 при .

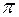2. В кристалле имеется поворотная ось второго порядка, совпадающая с осью 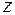ячейки

Если в кристалле имеется поворотная ось второго порядка, совпадающая с осью 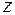ячейки, то атомы с координатами и 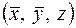объединяясь попарно дают:

.

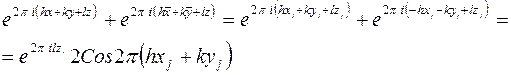Следовательно, формула структурной амплитуды будет иметь вид:

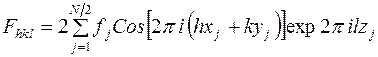(4)

или в тригонометрической форме

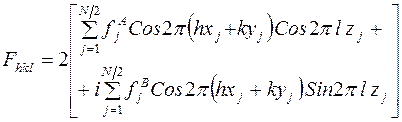. (5)

3. В кристалле есть плоскость симметрии 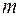, перпендикулярная оси 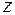и проходящая через начало координат.

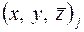В этом случае попарно объединяются атомы, расположенные в точках и .Преобразование следующее:

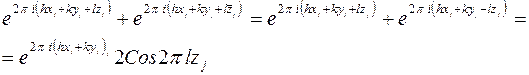
В этом случае формула структурной амплитуды преобразуется к виду:

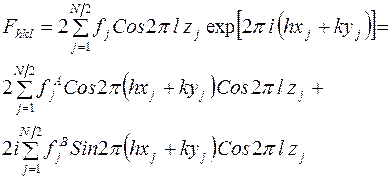. (6)

4. В кристалле присутствуют оси высшего порядка, винтовые оси и плоскости скользящего отражения.

Несколько сложнее преобразование формул в присутствии осей высшего порядка, а также при наличии винтовых осей и плоскостей скользящего отражения. Например, плоскость скользящего отражения 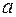, проходящая по координатной плоскости 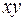, связывает атомы с координатам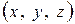и и 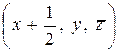. Соответственно этому объединяются члены

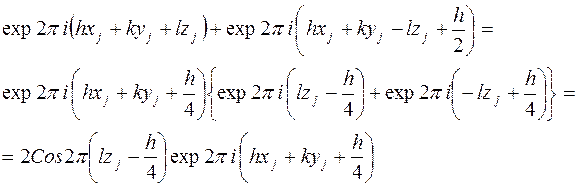
Получим

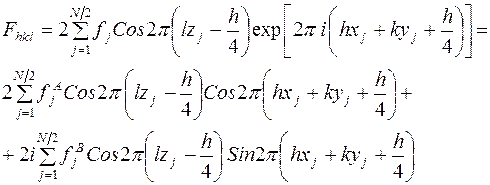. (7)

Формулы, отвечающие винтовым осям и плоскостям скользящего отражения, содержат в себе и правила погасаний, характеризующие соответствующие элементы симметрии. Так формула (7) приводит к условию 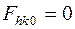при 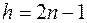, характеризующему присутствие плоскостей скользящего отражения. Действительно, положив 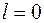, получим величину, обращающуюся в 0 при нечетных :

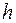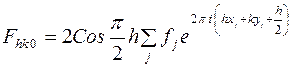(8)

Комбинация элементов симметрии приводит к дальнейшим видоизменениям формул.

Каждая пространственная группа симметрии характеризуется своей преобразованной формулой, которая и служит исходным пунктом при практических расчетах структурных амплитуд. Соответствующие данные приводятся в справочниках по рентгеноструктурному анализу или в специальных таблицах для рентгеновской кристаллографии.

Обычно предполагается, что формула приведена к виду:

(9)

И в справочнике даются лишь выражения 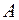и 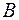вещественной и мнимой части тригонометрических множителей при атомных амплитудах.

Результаты монокристальных исследований являются основой для определения координат атомов.