Принимается, что объем , содержащий заряд , рассеивает волну, амплитуда которой равна рассеиваемой электроном амплитуде, но умноженной на .
Элементарные волны, рассеиваемые всем объемом, в котором распределен заряд электронов, интерферируют между собой и между ними имеется разность фаз, зависящая от взаимного расположения «источников», т.е. дифференциальных  .
.
Если бы амплитуды всех волн складывались, то суммарная интенсивность равнялась бы 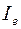 (формула Томсона). На самом деле за счет интерференции интенсивность уменьшается до
(формула Томсона). На самом деле за счет интерференции интенсивность уменьшается до
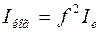 ,
,
причем
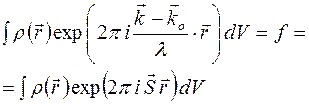 (1)
(1)
где 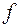 - фактор рассеяния атомного электрона,
- фактор рассеяния атомного электрона, 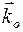 ,
, 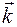 - единичные векторы падающего и рассеянного лучей. Дробь
- единичные векторы падающего и рассеянного лучей. Дробь 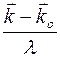 обозначили
обозначили  . Интеграл распространяется на весь объем атома, в котором
. Интеграл распространяется на весь объем атома, в котором 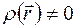 .
.
Если атом сферически симметричен, т.е. электронная плотность 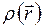 определяется только расстоянием от центра
определяется только расстоянием от центра 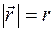 . Если между сферами радиуса
. Если между сферами радиуса  и
и 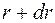 заключен заряд
заключен заряд 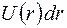 (в электронах), то (1) запишется в виде
(в электронах), то (1) запишется в виде
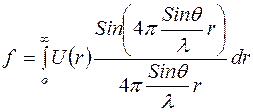 . (2)
. (2)
Согласно (2), величина 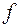 зависит только от
зависит только от 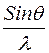 .
.
При изменении длины волны меняется и шкала углов рассеяния. При уменьшении 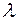 те же явления дифракции и интерференции наблюдаются под меньшими углами. Для
те же явления дифракции и интерференции наблюдаются под меньшими углами. Для 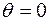 всегда
всегда 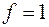 . С увеличением
. С увеличением 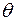 фактор
фактор 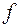 уменьшается и тем быстрее, чем протяженнее электронное облако (чем больше
уменьшается и тем быстрее, чем протяженнее электронное облако (чем больше  ).
).
При сильной связи электронов с ядром электронное облако не велико и значительная доля общего вклада вплоть до больших углов рассеяния приходится на когерентное рассеяние.
Для слабо связанных электронов когерентное рассеяние сосредоточено вдоль направлений, близких к первичному лучу.
Рассеяние атомом с несколькими электронами
В волновой механике при рассмотрении реального атома находятся волновые функции индивидуальных электронов, и принимается допущение, что общая электронная плотность равна сумме плотностей, соответствующих отдельным электронам. При этих условиях для когерентного рассеяния амплитуды волн, рассеянных электронами, складываются и суммарная интенсивность равна
 (1)
(1)
где 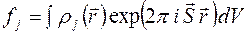 - амплитуда рассеяния
- амплитуда рассеяния 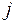 -того электрона, а
-того электрона, а 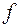 - атомная амплитуда рассеяния .
- атомная амплитуда рассеяния .
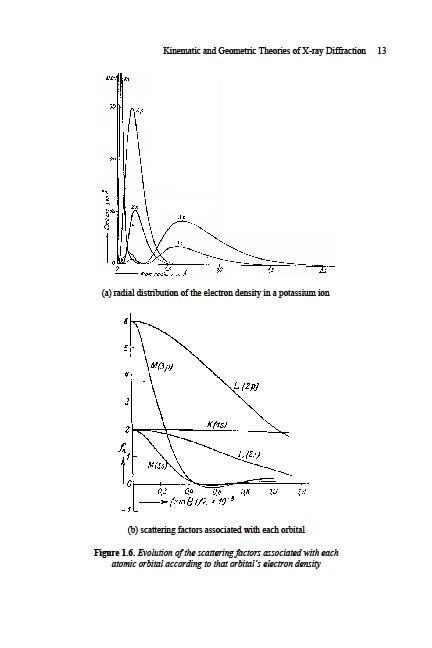
На рис.1 изображены радиальные распределения электронной плотности электронов последовательных оболочек иона калия 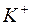 . На рис.2 представлены факторы рассеяния различных электронов иона
. На рис.2 представлены факторы рассеяния различных электронов иона 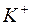 и фактор суммарного рассеяния иона
и фактор суммарного рассеяния иона 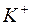 . Рассчитано методом Хартри (метод самосогласованного поля). Существуют еще приближения Томаса-Ферми.
. Рассчитано методом Хартри (метод самосогласованного поля). Существуют еще приближения Томаса-Ферми.
С «точки зрения» рентгеновского луча любое вещество представляет собой своеобразную конструкцию из непрерывной «электронной материи», причем каждая точка (xyz) имеет вполне определенное значение электронной плотности, которая изменяется непрерывно, а для кристаллов и периодично 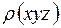 . Исходя из картины рассеяния Х-лучей, можно для кристаллов построить распределение электронной плотности, максимумы которого соответствуют координатам атомов.
. Исходя из картины рассеяния Х-лучей, можно для кристаллов построить распределение электронной плотности, максимумы которого соответствуют координатам атомов.
Аномалии фактора атомного рассеяния: эффект дисперсии
Формулу
 (1)
(1)
где
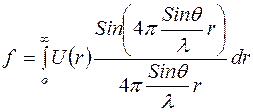 (2)
(2)
можно применять в тех случаях, когда частота излучения много больше частоты 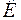 -края поглощения рассеивающего атома.
-края поглощения рассеивающего атома.
Если принять классическую модель атома, то можно сказать. Что при приближении частоты к критическому значению возникает явление резонанса и колебания, возбужденные в атоме падающей волной. Будут модулированы так же, как и рассеянное излучение. Поскольку длины волн Х-излучения, применяемого в структурном анализе, близки к скачкам поглощения часто встречающихся элементов, необходимо учитывать эффект «аномальной дисперсии», т.е. нужно учитывать, что величина 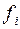 будет несколько отличаться от рассчитанной по формуле (2). Фактор атомного рассеяния принимается равным
будет несколько отличаться от рассчитанной по формуле (2). Фактор атомного рассеяния принимается равным
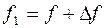 ,
,
где 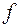 из формулы (2).
из формулы (2).
Величина поправки 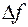 рассчитана на основе квантовой теории Хенкли и приводится в различных литературных источниках. Ее значение зависит от
рассчитана на основе квантовой теории Хенкли и приводится в различных литературных источниках. Ее значение зависит от 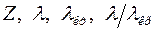 .
.
Учет аномалии фактора атомного рассеяния помогает различать в исследуемом кристалле элементы с последовательными атомными номерами (следовательно, очень близкими 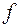 почти во всем интервале
почти во всем интервале 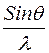 , например
, например 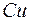 и
и 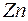 ).
).
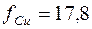
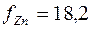 . Если применяем
. Если применяем 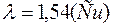 , то
, то 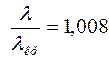
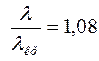 . Тогда
. Тогда
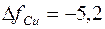
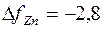 .
.
Учтем это и получим 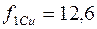 и
и 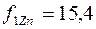 . Различие стало более заметным.
. Различие стало более заметным.
При исследовании с помощью рентгеноструктурного анализа кристаллических объектов мы имеем дело с дифракционным эффектом, возникающим при совместном рассеянии многими атомами благодаря их периодическому расположению – когерентным ансамблем.
1. При этом можно приближенно рассматривать атом, как точечный источник вторичных волн, амплитуда которых определяется числом электронов атома.
2. Предположить, что амплитуда вторичных волн одинакова во всех направлениях их распространения от атома.
Кроме того, предполагается, что:
1. атомы не совершают тепловых колебаний;
2. падающие лучи строго параллельны, монохроматичны (если не полихроматический пучок);
3. поглощения в кристалле нет;
4. кристалл имеет идеальное строение;
5. вторичные (рассеянные атомами) волны не взаимодействуют с атомами и падающей воной.
Сначала рассмотрим идеальный случай.
Рассеяние Х-лучей группой атомов
Имеем решетку, в которой атомы расположены только в узлах. Пучок Х-лучей падает на решетку в направлении 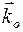 . Интенсивность дифрагированного пучка ≠0, если элементарные волны, рассеиваемые каждым атомом в направлении
. Интенсивность дифрагированного пучка ≠0, если элементарные волны, рассеиваемые каждым атомом в направлении 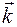 согласуются по фазе на любом фронте (плоскости) волны, перпендикулярном
согласуются по фазе на любом фронте (плоскости) волны, перпендикулярном 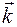


Рассмотрим рассеяние на двух атомах А и В, один из которых находится в начале координат, положение второго описывается однозначно межатомным вектором 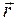 , который может быть выражен через его координаты относительно осей решетки
, который может быть выражен через его координаты относительно осей решетки 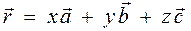 . Направление первичного пучка характеризуется единичным вектором
. Направление первичного пучка характеризуется единичным вектором 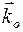 .
.
Предположим, что рассеивающая способность атомов для произвольного направления с единичным вектором 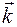 равна соответственно
равна соответственно 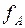 и
и 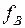 . При отсутствии разности хода для направления по первой и второй составляющей падающего луча общая рассеивающая способность равна
. При отсутствии разности хода для направления по первой и второй составляющей падающего луча общая рассеивающая способность равна
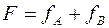 при
при 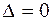
В направлении вдоль 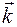 разность хода равна двух лучей
разность хода равна двух лучей
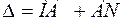 ,
,
где 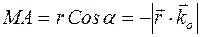 ,
,
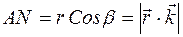 ,
,
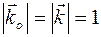 ,
,
то есть 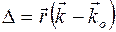 .
.
Разность фаз равна 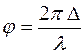 .
.
Для двух атомов можно записать 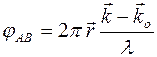 .
.
Обозначим  ,
,
тогда 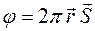 .
.
Согласно принципу суперпозиции амплитуда результирующей волны 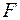 равна
равна
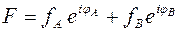 .
.
Считаем, что фаза луча, рассеянного атомом А, равна нулю, тогда 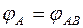 , т.е.
, т.е.
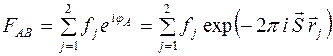
Аналогичные рассуждения можно выполнить для любой совокупности 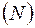 атомов. Получим
атомов. Получим
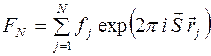 . (1)
. (1)
Эта формула отражает вполне определенный взгляд на строение вещества. Дискретное суммирование предполагает, что вещество состоит из отдельных структурных единиц (атомов, молекул и т.д.), рассеивающая способность которых известна и равна 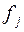 . Например, на рис.1 точку А можно рассматривать не как атом, а как молекулу с рассеивающей способностью
. Например, на рис.1 точку А можно рассматривать не как атом, а как молекулу с рассеивающей способностью 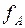 , или какой-нибудь химический радикал, или группу молекул. Эта особенность структурного анализа отражается понятием единичного рассеивающего центра.
, или какой-нибудь химический радикал, или группу молекул. Эта особенность структурного анализа отражается понятием единичного рассеивающего центра.
В качестве единичного рассеивающего центра можно рассматривать как электрон, так и точку с электронной плотностью 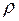 . При таком рассмотрении необходимо учитывать, что функция
. При таком рассмотрении необходимо учитывать, что функция 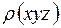 непрерывна и, используя вышеприведенную схему рассуждений, получим
непрерывна и, используя вышеприведенную схему рассуждений, получим
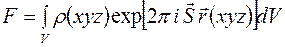 . (2)
. (2)
Интегрирование необходимо провести по всему объему кристалла.
Формула (2) может быть использована и для отдельного атома. Тогда для 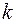 -того атома
-того атома
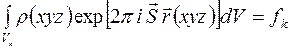 . (3)
. (3)
Начало координат совмещено с центром атома, интегрирование осуществляется по всему объему 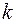 -того атома
-того атома 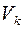 .
.
Весь объем рассеивающего объекта можно представить суммой отдельных атомов. Возражение, что атомы (сферические) не охватывают весь объем, не является принципиальным, так как любую точку в веществе можно отнести к вполне определенному атому.
Тогда формула (2) может быть преобразована
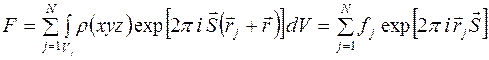 , (4)
, (4)
где вектор 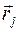 описывает положение атома относительно выбранного начала координат, а вектор
описывает положение атома относительно выбранного начала координат, а вектор 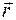 описывает область, относящуюся к этому атому.
описывает область, относящуюся к этому атому.
Следовательно, формулы (1) и (2) абсолютно тождественны. Кажущееся их различие объясняется только разным выбором единичного рассеивающего центра. В первом случае - атом, во втором – точка с электронной плотностью 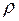 соответственно.
соответственно.
Отметим, что формулы (1) и (2) получены без каких-либо оговорок о структуре объекта, т.е. (1) и (2) справедливы как для кристаллических, так и для аморфных веществ.
Обратное пространство и дифракция Х-лучей на кристаллах
Формулы рассеивающей способности
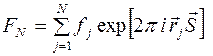
для совокупности 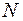 атомов и
атомов и
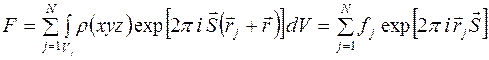 ,
,
где в качестве рассеивающего центра берется точка 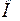 , в которой
, в которой 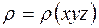 , описывают рассеивающую способность объекта с произвольной структурой не только как функцию состава и строения, что отражено значениями
, описывают рассеивающую способность объекта с произвольной структурой не только как функцию состава и строения, что отражено значениями 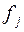 и векторами
и векторами 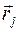 , но и как функцию вектора
, но и как функцию вектора 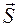 , природа которого пока не обсуждалась.
, природа которого пока не обсуждалась.
Известно, что геометрически расположение атомов в кристалле можно изобразить с помощью совокупности узловых плоскостей с определенными межплоскостными расстояниями 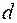 и индексами
и индексами 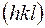 (рис.1). На рис.1 изображена одна из серий таких плоскостей с межплоскостным расстоянием
(рис.1). На рис.1 изображена одна из серий таких плоскостей с межплоскостным расстоянием 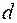 . Предположим, что узловая плоскость отражает Х-лучи зеркально, т.е. угол падения равен углу отражения. Пусть на кристалл падает Х-луч под углом скольжения
. Предположим, что узловая плоскость отражает Х-лучи зеркально, т.е. угол падения равен углу отражения. Пусть на кристалл падает Х-луч под углом скольжения 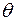 . Частично он отражается от первой плоскости, частично – от второй и т.д. Для получения максимума отражения необходимо, чтобы разность хода первого и второго лучей равнялась целому числу
. Частично он отражается от первой плоскости, частично – от второй и т.д. Для получения максимума отражения необходимо, чтобы разность хода первого и второго лучей равнялась целому числу 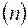 длин волн
длин волн 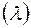 .
.
 |
Рисунок 1. Дифракция рентгеновских лучей в кристалле
Разность хода из рис.1 равна 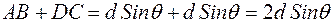 .
.
Следовательно, при отражении должно выполняться условие
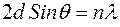 . (1)
. (1)
Одна и та же серия узловых плоскостей может дать несколько отражений, т.к. при изменении угла 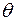 условие (1) может выполняться при других (тоже целочисленных) значениях
условие (1) может выполняться при других (тоже целочисленных) значениях  . При рассмотрении всей этой совокупности отражений (рефлексов) можно говорить о первом, втором и последующих порядках отражений.
. При рассмотрении всей этой совокупности отражений (рефлексов) можно говорить о первом, втором и последующих порядках отражений.
В структурном анализе обычно применяется несколько иной прием. Формула (1) записывается в виде
 , (2)
, (2)
где 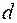 имеет тот же смысл, что и
имеет тот же смысл, что и 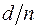 в формуле (1), но в данном случае можно считать, что отражения относятся к разным плоскостям, т.е. каждое отражение можно сопоставить со «своей» кристаллографической плоскостью. Если для первого порядка отражений плоскость имеет индексы
в формуле (1), но в данном случае можно считать, что отражения относятся к разным плоскостям, т.е. каждое отражение можно сопоставить со «своей» кристаллографической плоскостью. Если для первого порядка отражений плоскость имеет индексы 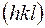 , то для
, то для  -го они равны
-го они равны 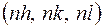 .
.
Уравнение (1) – уравнение Вульфа-Брэггов.
Для уточнения физического смысла вектора 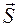 выполним следующее построение, предложенное Эвальдом и носящее его имя. Построение Эвальда позволяет определить направление дифрагированного луча, если на произвольно, го определенным образом ориентированный кристалл, направить пучок Х-лучей с длиной волны
выполним следующее построение, предложенное Эвальдом и носящее его имя. Построение Эвальда позволяет определить направление дифрагированного луча, если на произвольно, го определенным образом ориентированный кристалл, направить пучок Х-лучей с длиной волны 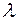 .
.
Вокруг образца проведем сферу радиусом  , сферу Эвальда (рис.2).
, сферу Эвальда (рис.2).
Направим первичный луч вдоль МО. Если ввести единичный вектор 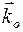 , то
, то 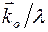 является вектором падающего луча. Нас интересует луч, рассеянный в произвольном направлении, которое определено радиусом-вектором
является вектором падающего луча. Нас интересует луч, рассеянный в произвольном направлении, которое определено радиусом-вектором 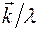 (
( 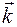 - единичный вектор направления рассеяния). Конец вектора
- единичный вектор направления рассеяния). Конец вектора 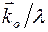 считаем началом обратной решетки кристалла, которая может поворачиваться вокруг
считаем началом обратной решетки кристалла, которая может поворачиваться вокруг 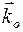 при неподвижной сфере Эвальда. На сферу Эвальда при этом могут попадать узлы обратной решетки.
при неподвижной сфере Эвальда. На сферу Эвальда при этом могут попадать узлы обратной решетки.
Если мы действительно обнаружим рефлекс в направлении ОВ, значит угол АОВ равен 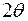 . Следовательно, АВ является нормалью к узловой плоскости, от которой получено отражение (след этой плоскости на рис.2 обозначен линией ОС).
. Следовательно, АВ является нормалью к узловой плоскости, от которой получено отражение (след этой плоскости на рис.2 обозначен линией ОС).
 |
Из
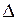 АОВ следует
АОВ следует 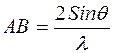 , т.е.
, т.е. 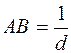 ,
, 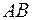 ┴
┴ 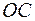 , значит вектор
, значит вектор 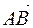 есть вектор обратной решетки отражающей плоскости и одновременно это искомый вектор
есть вектор обратной решетки отражающей плоскости и одновременно это искомый вектор 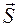 . Следовательно, если плоскость находится в отражающем положении, то ее узел обратного пространства находится на сфере Эвальда. Справедливо и обратное утверждение: если узел плоскости не находится на сфере Эвальда, то рефлекса от нее на рентгенограмме не получится.
. Следовательно, если плоскость находится в отражающем положении, то ее узел обратного пространства находится на сфере Эвальда. Справедливо и обратное утверждение: если узел плоскости не находится на сфере Эвальда, то рефлекса от нее на рентгенограмме не получится.
Для возникновения отраженного пучка необходимо чтобы точка В совпала с узлом обратной решетки. Дифрагированные лучи возникают, когда узлы обратной решетки оказываются на сфере Эвальда. Направление лучей определяется векторами, соединяющими центр сферы с узлами на ее поверхности.
Если кристалл находится в случайном положении, то на поверхности сферы Эвальда может не оказаться узлов обратной решетки и отражений не будет.
Уравнение
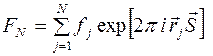 (3)
(3)
может быть использовано для любых объектов, в том числе и для кристаллических. Для кристаллов
 , (4)
, (4)
где 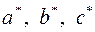 - параметры элементарной ячейки в обратном пространстве,
- параметры элементарной ячейки в обратном пространстве, 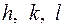 - индексы Миллера (координаты узла в обратном пространстве);
- индексы Миллера (координаты узла в обратном пространстве);
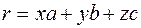 , где
, где 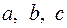 - параметры элементарной ячейки кристалла,
- параметры элементарной ячейки кристалла, 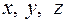 - относительные координаты (атома). Учитывая зависимость между
- относительные координаты (атома). Учитывая зависимость между 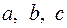 и
и 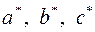 получим
получим
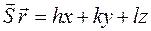 . (5)
. (5)
т.е. для кристалла (правильнее – для одной элементарной ячейки)
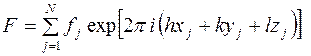 (6)
(6)
Величина 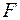 называется структурной амплитудой, она строго связана с определенной узловой плоскостью, так как определяется теми же индексами
называется структурной амплитудой, она строго связана с определенной узловой плоскостью, так как определяется теми же индексами 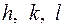 . Для каждого кристалла существует свой набор
. Для каждого кристалла существует свой набор 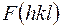 . Если все эти амплитуды изобразить в соответствующей системе координат, то совокупность этих точек и определит обратную решетку данного кристалла. Каждый узел обратного пространства описывается не только тремя координатами
. Если все эти амплитуды изобразить в соответствующей системе координат, то совокупность этих точек и определит обратную решетку данного кристалла. Каждый узел обратного пространства описывается не только тремя координатами 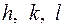 (в единицах
(в единицах 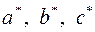 ), но и «весовым» множителем
), но и «весовым» множителем 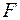 . Чем больше значение
. Чем больше значение 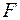 у точки, вышедшей на сферу Эвальда, тем сильнее будет соответствующий ей рефлекс. Тем выше будет его интенсивность.
у точки, вышедшей на сферу Эвальда, тем сильнее будет соответствующий ей рефлекс. Тем выше будет его интенсивность.
Для идеального кристалла обратное пространство сконцентрировано в его узлах. Плотность пространства в любой точке вне узла равна нулю. Если эти не узловые точки находятся на сфере Эвальда, то 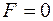 и рассеяния нет.
и рассеяния нет.
Для аморфных объектов в обратном пространстве наблюдаются «ненулевые» значения «плотности» этого пространства в любой точке.
Т.е.для кристаллов обратное пространство прерывисто (дискретно, дисконтинуально) , для аморфных веществ – непрерывно (континуально).
Рассеяние Х-лучей идет по направлениям радиусов-векторов сферы Эвальда для точек обратного пространства с ненулевой «плотностью». Следовательно рентгенограмма неподвижных монокристаллов – совокупность точек. От аморфных объектов наблюдается непрерывное (не обязательно равномерное) изменение интенсивности по всем углам рассеяния.
Выражение (6) может быть представлено в тригонометрической форме

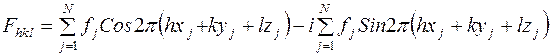 (7)
(7)
Интенсивность дифрагированного луча пропорциональна квадрату его амплитуды, т.е. квадрату модуля 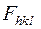
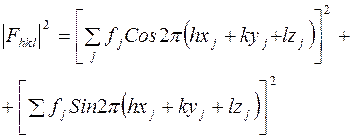 (8)
(8)
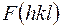 зависит от выбранного начала координат (ячейки кристалла), так как в это выражение входят координаты атомов
зависит от выбранного начала координат (ячейки кристалла), так как в это выражение входят координаты атомов 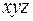 , а модуль
, а модуль 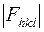 от них не зависит. Можно записать
от них не зависит. Можно записать
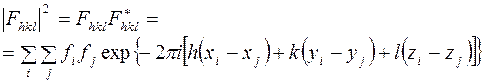 . (9)
. (9)
В выражение (9) входят только взаимные расстояния между атомами.
__________________________________________________________________
Каждое семейство параллельных сеток (плоскостей решетки) определяет дискретную совокупность направлений селективных отражений. Для удобства рассмотрения дифракционных картин т взаимосвязи их со структурой изучаемых кристаллов наличие теории, связывающей в простой форме направления селективных отражений и кристаллографические направления. Такая теория создана Лауэ и Эвальдом, она основана на чисто геометрическом понятии «обратной решетки».
Построение обратной решетки
Из произвольной точки проводятся три вектора 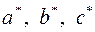 . Вектор
. Вектор 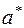
параллелен семейству плоскостей параллельных векторам 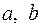 кристаллической решетки. Длина вектора
кристаллической решетки. Длина вектора 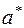 равна
равна 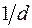 (обратно межплоскостному расстоянию этого семейства плоскостей). Для векторов кристаллической решетки и обратной решетки должны выполняться условия: скалярные произведения:
(обратно межплоскостному расстоянию этого семейства плоскостей). Для векторов кристаллической решетки и обратной решетки должны выполняться условия: скалярные произведения:
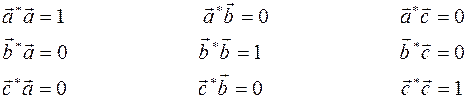 (1)
(1)
Любой вектор  перпендикулярен к плоскости кристаллической решетки
перпендикулярен к плоскости кристаллической решетки 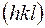 , а его длина обратна величине
, а его длина обратна величине 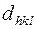 .
.
Соответствие между двумя решетками, их взаимосвязь не зависит от выбранной элементарной ячейки.
Если построить решетку, обратную обратной решетке, то получится исходная (прямая) решетка. Равенства (1) запишутся в виде:
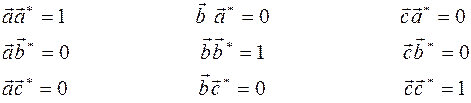 ,
,
т.е. вектор 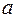 получается из обратной решетки так же как
получается из обратной решетки так же как 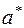 из решетки прямой. Зависимость объемов
из решетки прямой. Зависимость объемов 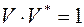 также симметрична. Узлы обратной решетки, индексы которых не являются взаимно простыми числами
также симметрична. Узлы обратной решетки, индексы которых не являются взаимно простыми числами 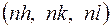 , соответствуют семействам плоскостей, параллельных плоскости
, соответствуют семействам плоскостей, параллельных плоскости 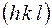 , но с межплоскостными расстояниями в
, но с межплоскостными расстояниями в  раз меньше, чем
раз меньше, чем 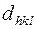 .
.
Дата добавления: 2015-08-20; просмотров: 859;
