Интенсивность рассеянного луча определяет рассеивающую способность объекта.

В качестве масштаба рассеивающей способности выбирается интенсивность рентгеновского луча, рассеянного на свободном электроне. Т.е. если интенсивность падающего на объект луча равна , а в каком-то направлении интенсивность рассеянного луча , то для определения рассеивающей способности объекта вместо него надо поставить свободный электрон, направить на него луч той же интенсивности и найти интенсивность рассеянного луча. Понятно, что экспериментально это выполнить невозможно, но можно осуществить расчетным путем.

Иногда рассеивающую способность оценивают не по интенсивности, а по величине амплитуды 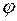рассеянного луча. При этом 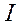~ 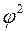. Поэтому, говоря о рассеивающей способности необходимо уточнить – по какой величине она определена: 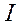(интенсивности) или 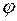(амплитуде) рассеянного луча.

Рассеивающая способность электрона равна единице.

Если в системе есть несколько электронов, то рассеивающая способность такой системы может принимать различные значения в зависимости от взаимного расположения электронов.

Интерференция

Если в одном направлении распространяются две волны (или несколько), то амплитуда, а, следовательно, и интенсивность суммарной волны может быть различной в зависимости от разности фаз налагающихся волн. Это явление интерференции. Оно имеет место в том случае, когда колебания волн когерентны (согласованы), т.е. происходят в одной и той же плоскости и сохраняют все время одну и ту же разность фаз.

Дифракционный эффект

Рассмотрим результат взаимодействия Х-луча с двумя электронами, находящимися на расстоянии 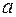друг от друга. На них вдоль 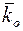падает плоская Х-волна. В направлении первичного луча рассеивающая способность системы равна 2. так как разность хода (разность фаз) для первой и второй составляющей пучка равна нулю. В произвольном направлении 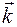рассеивающая способность системы может быть различной. На рис. 3б

рассеивающая способность в направлении 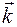равна нулю, т.к. две составляющие находятся в противофазе. Следовательно, система из двух электронов характеризуется рассеивающей способностью, изменяющейся в интервале от нуля до двух. Очевидна ее зависимость от угла 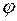. При дальнейшем увеличении угла 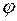сдвиг по фазе еще увеличится, что приведет к возрастанию амплитуды результирующей волны. При разности фаз в один полный период (разности хода лучей в одну длину волны) амплитуда достигнет максимального значения и т.д. будет повторение. На рис.4 изображена зависимость интенсивности результирующего луча от угла отклонения. Такая зависимость амплитуды, а, следовательно, и интенсивности результирующей волны от направления вследствие интерференции вторичных волн называется дифракционным эффектом.

Рассеяние Х-лучей парой электронов. Частный случай дифракции

Если система неупорядочена (газ), то дифракционного эффекта не наблюдается, картина размазывается (идет рассеяние).

При прохождении рентгеновских лучей через кристаллы, благодаря правильно периодическому расположению атомов, на первое место выступает дифракционный эффект. Если в атоме электронов, то в направлении падающего луча рассеивающая способность численно равна , а с увеличением угла между падающим и рассеянным лучом начинает уменьшаться.

Рис.4 Угловая зависимость интенсивности дифрагированных лучей от: а) для пары электронов; б) бесконечной цепочки электронов.

Рассеяние атомом

Рассеяние лучей отдельным атомом представляет собой сложное интерференционное явление – накладываются волны, рассеянные электронами, находящимися в разных частях атома.

Длина волны рентгеновских лучей и размеры атомов таковы, что рассеивающая способность не уменьшается до нуля, а даже при наибольшей разности хода имеет ненулевые значения. Рассеивающая способность атомов зависит не только от величины , но и от длины волны 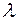и направления рассеянного луча.

Обычно рассеивающую способность рассматривают как функцию аргумента 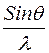, где 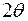угол между направлением падающего и рассеянного лучей.

Атомная амплитуда – это амплитуда Х-луча, рассеянного на атоме, выраженная в электронных единицах. Эта величина обозначается 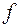. Величина 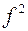называется атомным фактором и определяет интенсивность луча, рассеянного на атоме.

Термин «рассеивающая способность» объединяет величины 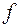и .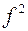

Понятие электронной плотности

Принятое в квантовой механике понятие электронной плотности находит широкое применение в рентгеноструктурном анализе.

В волновой механике точечный электрон классической теории заменяется диффузным распределением электрического заряда. Принимая за единицу заряд электрона, плотность этого облака 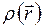в точке возле ядра, определяемой вектором 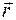, равна 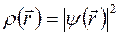, где 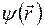- волновая функция, определяемая уравнением Шредингера.