Эффект максимального поглощения излучения определенных длин волн называется селективным поглощением.

Фильтры рентгеновского излучения

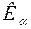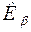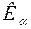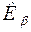1. Эффект селективного поглощения широко используется для отделения линий от . На пути лучей ставится тонкий слой вещества содержащего атомы, край полосы поглощения которых лежит между и линиями излучения. При этом 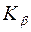линия будет ослаблена во много раз сильнее, чем .

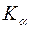2. Вещество фильтра должно иметь номер на единицу меньше, чем атомный номер излучателя.

3. Величина ослабления будет обусловлена толщиной фильтра – количеством материала ослабителя на пути излучения.

4. Фильтр должен располагаться вне камеры. В противном случае за счет флюоресценции материала фильтра будет повышаться уровень фона (вуаль на пленках).

Экраны-фильтры изготавливаются обычно так, чтобы отношение интенсивносте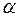й и 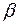излучения равнялось 1/600.

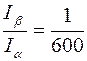т.е. .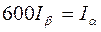

Фильтры можно готовить из фольги чистого элемента или из его порошка, закрепленного на бумаге. В первом случае основной характеристикой фильтра является его толщина, во втором – количество вещества, приходящееся на единицу пути (плотность, поделенная на толщину).

В таблице приведены характеристики фильтров для различных длин волн (анодов): материал фильтра, его толщина ( 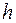), двумерная плотность ( 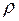), длина волны К-полосы поглощения ( 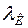) и коэффициент прохождения 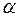-линии анода ( ).

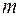Таблица

Основные характеристики селективных фильтров для 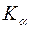- излучения

Материал анода	Характеристики фильтров
Материал фильтра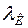
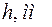
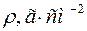
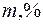
Хром	Ванадий	2,968	0,016	0,009
Железо	Марганец	1,895	0,016	0,012
Кобальт	Железо	1,743	0,018	0,014
Никель	Кобальт	1,608	0,018	0,015
Медь	Никель	1,487	0,021	0,018
Молибден	Цирконий	0,688	0,108	0,069
Серебро	Родий	0,534	0,079	0,096

Если взять два фильтра, элементы которых расположены рядом в периодической таблице, то их коэффициенты массового поглощения практически совпадут везде, кроме области, расположенной между краями поглощения. Если получить рентгенограмму сначала при одном (с меньшим 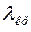), а затем при установке обоих, то эти рентгенограммы будут отличаться тем, что на второй рентгенограмме отсутствует участок спектра между 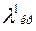и 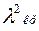, а на первой он есть. Такие двойные фильтры (фильтры Росса) находят широкое применение в практике рентгеноструктурных исследований, практически выполняя роль монохроматоров.

Физиологическое действие Х-лучей

Рентгеновские лучи влияют на характер биохимических реакций, протекающих в живых тканях. Под их действием происходит расщепление молекул воды на водород и гидроксил – частицы чрезвычайно активные в химическом отношении. Вследствие этого нарушается нормальный ход биохимических процессов в организме.

В живых организмах они могут вызвать местное (ожог, затрагивающий покровные ткани и даже мышцы) или общее поражение (лучевую болезнь разной степени тяжести)

Для живых организмов наибольшую опасность представляет мягкое рентгеновское излучение, так как оно в большей степени поглощается живыми тканями, состоящими в основном из легких элементов.

Когерентное рассеяние Х-лучей

Всякое вещество, на которое падают Х-лучи, испускают вторичное излучение, длина которого равна первичной длине волны, либо близка к ней.

1. В случае рассеяния без изменения длины волны все атомы вещества образуют ансамбль когерентных источников, излучение которых может интерферировать

2. Благодаря тому, что в конденсированных средах межатомные расстояния по порядку величины равны длинам волн Х-лучей, возможна интерференция.

3. Энергия рассеяния не распределяется по всему пространству, а

4. концентрируется по отдельным направлениям, где рассеяние наиболее интенсивное – получаются дифракционные картины, по которым возможно определить взаимное расположение атомов.

На этих трех фактах основан рентгеноструктурный анализ. В основе рентгеноструктурного анализа лежит явление когерентного рассеяния Х-лучей конденсированными средами.

Рассеяние свободным электроном. Формула Томсона

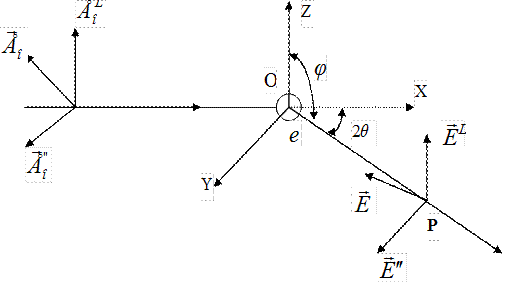
Пусть волна плоско поляризованная, электрический вектор ее 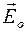распространяется по , встречает в точке О свободный электрон (рис.). Под действием переменного ускорения электрон начнет колебаться с амплитудой

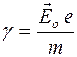. (1)

При этом он будет испускать электромагнитное излучение, которое в точке Р опишется вектором

, (2)

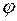где - расстояние ОР, - угол между ОР и вектором ускорения электрона 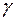, электрический вектор лежит в плоскости ( 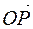, 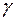). Т.е., в точку Р попадет излучение с амплитудой

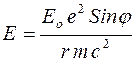. (3)

Выберем в качестве плоскости ХОУ плоскость, в которой лежат векторы 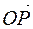, 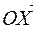. Пусть угол рассеяния равен 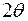. Предположим, что в начальный момент времени вектор 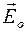направлен по OZ нормально к плоскости

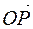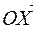, . Тогда 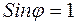и

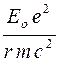E_┴= (4)

Отношение интесивностей волны первичной (в точке О) и рассеянной (в точке Р) равно отношению квадратов амплитуд электрических полей

I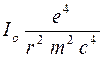_┴ = , т.к. 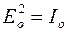(5)

I_┴ - поток энергии, пересекающий за 1 с площадь 1 см², расположенную в точке Р перпендикулярно 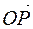. Эта площадь видна из точки О под телесным углом равным 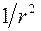. Энергия рассеянного излучения, отнесенная к единице угла, будет

I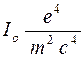_┴ = . (6)

Если предположить теперь, что первичный электрический вектор расположен в плоскости ХОУ, то, согласно (3) и (6) интенсивность в точке Р будет

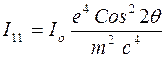. (7)

Поляризованный пучок всегда может быть разложен на два пучка, электрические векторы которых перпендикулярны и параллельны плоскости ХОУ в пропорции k_┴ и 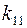, k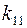_┴+ =1. Тогда интенсивность рассеяния можно представить в виде

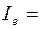k_┴ I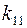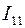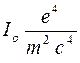_┴+ = (k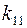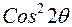_┴+ ) . (8)

Если первичный пучок не поляризован, то k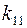_┴ = =1/2, тогда (8) примет вид

(9)

Это формула Томсона.

При подстановке 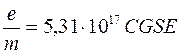, , 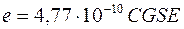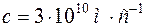получим

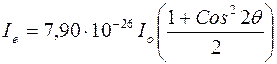. (10)

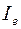- энергия рассеяния внутри единицы телесного угла.

Интенсивность рассеяния пучка на расстоянии от точки рассеяния равна .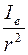

Формулы (8) и (9) являются фундаментальными в рентгеноструктурном анализе, т.к. все теоретические расчеты сводятся к определению рассеивающей способности данного объекта.

Применительно к ядру: интенсивность рассеяния одним протоном будет в 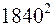раз слабее интенсивности рассеяния одним электроном. Этой величиной можно пренебречь.