МЕТОД ФУРЬЕ
Структурная амплитуда может быть представлена двумя формами записи (см. формулы (25)–(31)):
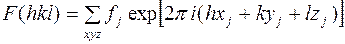 ; (1)
; (1)
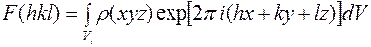 .
.
Обе эти формулы отражают одинаковый физический смысл, но учитывают различный подход к рассеивающим центрам. Первая формула в качестве единичных рассеивающих центров рассматривает атомы, расположенные дискретно, т. е. в строго определенных точках с координатами 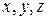 . Вторая формула предполагает в качестве единичных рассеивающих центров точки с электронной плотностью
. Вторая формула предполагает в качестве единичных рассеивающих центров точки с электронной плотностью 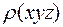 , которые образуют континуум.
, которые образуют континуум. 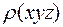 – непрерывная функция, имеющая трехмерную периодичность с периодом
– непрерывная функция, имеющая трехмерную периодичность с периодом 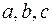 и во всех точках дифференцируема по координатам
и во всех точках дифференцируема по координатам 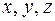 .
.
Для иллюстрации метода Фурье, широко используемого для исследования структур кристаллов, рассмотрим одномерный случай, когда электронная плотность изменяется только вдоль одного направления 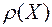 . Запись
. Запись 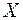 (икс большое) означает, что взята абсолютная координата вдоль ребра а элементарной ячейки.
(икс большое) означает, что взята абсолютная координата вдоль ребра а элементарной ячейки.
Итак, 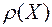 функция непрерывна, дифференцируема и периодична, следовательно, ее можно разложить в ряд Фурье.
функция непрерывна, дифференцируема и периодична, следовательно, ее можно разложить в ряд Фурье.
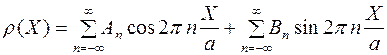 . (2)
. (2)
Коэффициенты этого разложения, как это показано в соответствующем разделе математического анализа, имеют вид:
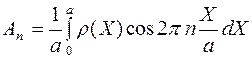 ,(3)
,(3)
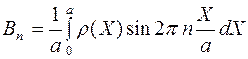
ряд (2) можно представить в несколько иной форме. Введем вместо 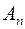 и
и 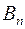 новые коэффициенты
новые коэффициенты 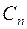 и
и 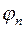 , связанные с
, связанные с 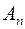 и
и 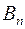 соотношениями:
соотношениями:
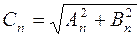 ,
,
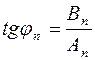 . (4)
. (4)
Отсюда вытекает
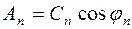 , (5)
, (5)
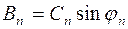 .
.
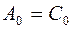
Следовательно,
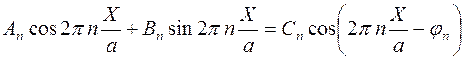 ,
,
и формула (2) примет вид:
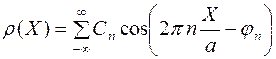 . (6)
. (6)
Для преобразования формулы (6) воспользуемся формулой Эйлера
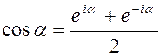 .
.
Рассмотрим выражение под знаком суммы в (6)
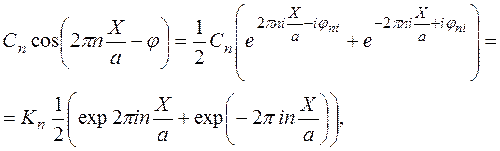
где 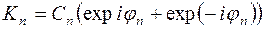 .
.
Заметим, что  , т.к.
, т.к. 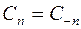 . Учитывая это, получим:
. Учитывая это, получим:
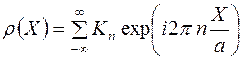
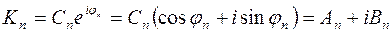 (7)
(7)
и 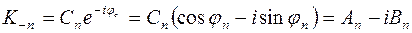
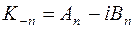 .
.
Учитывая формулу (3), запишем:
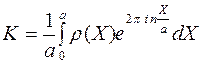 . (8)
. (8)
Перейдем от абсолютной координаты 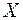 к относительной
к относительной 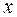 .
. 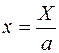 ,
, 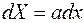 и заменим
и заменим 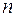 на
на 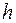 . Пределы интегрирования в этом случае станут 0 и 1.
. Пределы интегрирования в этом случае станут 0 и 1.
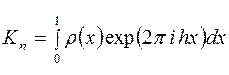 . (8а)
. (8а)
Трехмерная функция 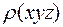 также может быть разложена в ряд, аналогичный ряду (7).
также может быть разложена в ряд, аналогичный ряду (7).
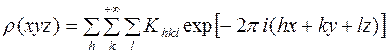 , (9)
, (9)
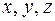 – относительные координаты атомов;
– относительные координаты атомов;
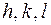 – целые числа, причем, согласно выражению (8а).
– целые числа, причем, согласно выражению (8а).
Будем иметь, согласно (8а)
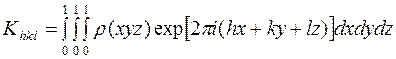 ,
,
или
 . (10)
. (10)
Сравнивая формулы (10) и (1), убеждаемся, что 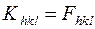 .
.
Итак, нами получена взаимосвязь между 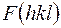 и
и 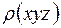
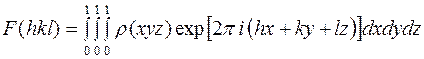 , (11)
, (11)
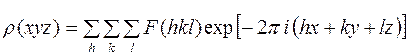 .
.
Связанные таким образом функции называются трансформантами Фурье. Если известна формула для расчета 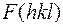 , то формула для расчета
, то формула для расчета 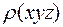 получается ее Фурье-трансформированием, т. е. надо поменять знак суммы на интеграл (или наоборот).
получается ее Фурье-трансформированием, т. е. надо поменять знак суммы на интеграл (или наоборот).
Используя ряд (11), можно по экспериментальным значениям 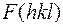 рассчитать электронную плотность в любой точке, а максимальное значение электронной плотности соответствует координате атома.
рассчитать электронную плотность в любой точке, а максимальное значение электронной плотности соответствует координате атома.
В принципе можно определить не только координаты атома, но и их порядковый номер, так как высота максимума электронной плотности зависит от числа электронов в атоме (пропорциональна 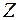 ).
).
Физический смысл разложения электронной плотности в ряд Фурье
Итак, для нахождения электронной плотности необходимо рассчитать ряд Фурье, коэффициентами которого являются структурные амплитуды. Для расчета 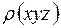 можно использовать одну из трех, тождественных друг другу, форм записи формулы (11)
можно использовать одну из трех, тождественных друг другу, форм записи формулы (11)
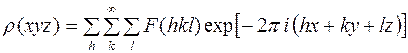 (12)
(12)
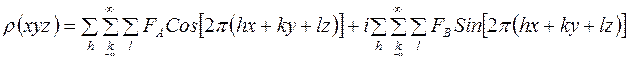 (13)
(13)
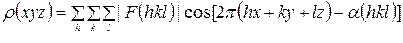 , (14)
, (14)
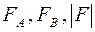 – действительная, мнимая части и модуль структурной амплитуды соответственно,
– действительная, мнимая части и модуль структурной амплитуды соответственно, 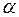 – фаза структурной амплитуды.
– фаза структурной амплитуды.
Каждый член ряда ((12)–(14)) представляет собой гармоническую волну, и по смыслу, и по размерности соответствующую электронной плотности.
Рассмотрим одно из слагаемых ряда 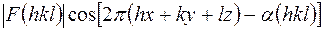 , которое строго соответствует определенной кристаллографической плоскости
, которое строго соответствует определенной кристаллографической плоскости 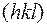 . Причем, если
. Причем, если 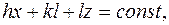 то электронная плотность имеет одно и то же значение. Изменяя
то электронная плотность имеет одно и то же значение. Изменяя 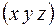 , получаем серию параллельных плоскостей, в каждой из которых электронная плотность постоянна.
, получаем серию параллельных плоскостей, в каждой из которых электронная плотность постоянна.
Следовательно, каждое слагаемое в правой части рядов (12)–(14) действительно описывает волну электронной плотности вдоль направления, перпендикулярного плоскости 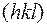 .
.
Известно, что
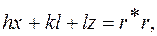
где 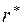 – вектор обратной решетки;
– вектор обратной решетки; 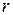 – вектор кристаллического пространства.
– вектор кристаллического пространства.
Поскольку 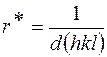 , то период электронной волны равен
, то период электронной волны равен 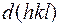 .
.
Итак, каждый член суммы есть гармоническая волна электронной плотности вдоль нормали к плоскости 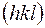 ,
, 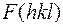 - амплитуда этой волны, а
- амплитуда этой волны, а 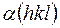 - ее фаза. Весь кристалл представляет собой совокупность таких волн, которые пронизывают вещество во всех направлениях, и при их взаимном наложении возникают максимумы электронной плотности с координатами, совпадающими с координатами атомов. Каждая такая волна строго приписывается к плоскости
- ее фаза. Весь кристалл представляет собой совокупность таких волн, которые пронизывают вещество во всех направлениях, и при их взаимном наложении возникают максимумы электронной плотности с координатами, совпадающими с координатами атомов. Каждая такая волна строго приписывается к плоскости 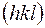 , т.к. ее можно отнести к рефлексам, отвечающим индексам
, т.к. ее можно отнести к рефлексам, отвечающим индексам 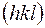 и
и 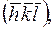 причем модули их амплитуд равны
причем модули их амплитуд равны 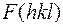 , фазы -
, фазы - 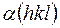 и
и 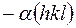 .
.
Каждая волна электронной плотности отвечает за свою пару отражений. Мешать друг другу при дифракции они не могут.
Структурная амплитуда является трансформантой электронной плотности. Как мы убедились, каждое отражение строго соответствует только одной волне электронной плотности, которая определяется плоскостью 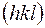 . Плоскость же в обратном пространстве изображается точкой, «вес» которой определяется величиной
. Плоскость же в обратном пространстве изображается точкой, «вес» которой определяется величиной 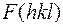 . Чем больше «вес» точки обратного пространства, тем сильнее будет этот рефлекс при выходе этой т очки на сферу Эвальда. В пространстве кристалла смысл «веса» точки
. Чем больше «вес» точки обратного пространства, тем сильнее будет этот рефлекс при выходе этой т очки на сферу Эвальда. В пространстве кристалла смысл «веса» точки 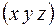 имеет ее электронная плотность
имеет ее электронная плотность 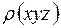 , определяемая суперпозицией вышеприведенных гармонических волн.
, определяемая суперпозицией вышеприведенных гармонических волн.
Определение положения атомов на распределении электронной плотности
Зная 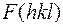 , можно определить
, можно определить 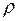 в любой точке с координатами
в любой точке с координатами 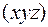 . Для определения положения атома необходимо найти точку
. Для определения положения атома необходимо найти точку 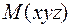 , где
, где 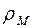 имеет максимальное значение. При случайном выборе точек расчета мы можем просто пропустить точку М. Для определения координат атомов придерживаются весьма простых правил, которые можно проиллюстрировать на примере двумерного Фурье-ряда:
имеет максимальное значение. При случайном выборе точек расчета мы можем просто пропустить точку М. Для определения координат атомов придерживаются весьма простых правил, которые можно проиллюстрировать на примере двумерного Фурье-ряда:
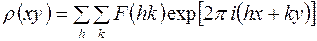 . (15)
. (15)
Пусть из эксперимента 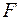 и
и 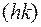 известны. Надо взять лист бумаги и в определенном масштабе изобразить параллелограмм, соответствующий элементарной (плоской) ячейке. Каждая сторона ячейки делится на n равных частей и через точки деления (
известны. Надо взять лист бумаги и в определенном масштабе изобразить параллелограмм, соответствующий элементарной (плоской) ячейке. Каждая сторона ячейки делится на n равных частей и через точки деления ( 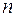 ) проводятся прямые, параллельные сторонам параллелограмма. Части каждых сторон неодинаковы по абсолютной величине, но их относительные величины равны. Проведя такое разделение, получим
) проводятся прямые, параллельные сторонам параллелограмма. Части каждых сторон неодинаковы по абсолютной величине, но их относительные величины равны. Проведя такое разделение, получим 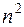 точек, координаты которых строго известны. Именно для этих точек и проводится расчет электронной плотности. При выборе числа n необходимо каждый раз исходить из учета линейных размеров рассматриваемой ячейки. Если
точек, координаты которых строго известны. Именно для этих точек и проводится расчет электронной плотности. При выборе числа n необходимо каждый раз исходить из учета линейных размеров рассматриваемой ячейки. Если 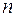 мало, то можно пропустить (просмотреть) атом, если же
мало, то можно пропустить (просмотреть) атом, если же 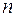 слишком велико, то увеличивается объем расчетной работы. Если, например, на рентгенограмме есть
слишком велико, то увеличивается объем расчетной работы. Если, например, на рентгенограмме есть 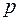 рефлексов, а
рефлексов, а 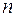 = 60, то надо суммировать 3600 рядов по
= 60, то надо суммировать 3600 рядов по 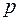 слагаемых в каждом. Если же n = 100, то уже надо суммировать 10 000 рядов.
слагаемых в каждом. Если же n = 100, то уже надо суммировать 10 000 рядов.
Рассчитав 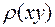 по всем точкам, прямо на листе бумаги проставляют численные значения этой функции. Одинаковые значения
по всем точкам, прямо на листе бумаги проставляют численные значения этой функции. Одинаковые значения  соединяют линией, называемой изолинией электронной плотности. Появляется как бы топографическая карта кристалла, только вместо высоты над уровнем моря стоит значение электронной плотности. На рис. дан пример такой карты электронной плотности кристалла слюды.
соединяют линией, называемой изолинией электронной плотности. Появляется как бы топографическая карта кристалла, только вместо высоты над уровнем моря стоит значение электронной плотности. На рис. дан пример такой карты электронной плотности кристалла слюды.
Становится понятно, почему структурная амплитуда может быть измерена в любых единицах. Произвольность выбора единицы измерения скажется на значении 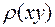 , но не на положении максимума этой функции
, но не на положении максимума этой функции
Построение трехмерной электронной плотности довольно трудоемко. Такую структуру нельзя изобразить на бумаге. Поэтому в структурном анализе большое применение находят различные сечения и проекции электронной плотности.
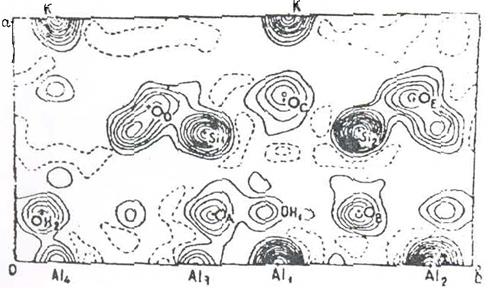
Рис. Карта электронной плотности (на примере слюды-мусковита)
Сечения электронной плотности
Предположим, что требуется найти сечение электронной плотности плоскостью, параллельной координатной плоскости 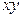 , проходящей на высоте z'. Следовательно, необходимо найти
, проходящей на высоте z'. Следовательно, необходимо найти
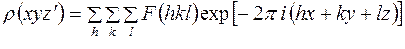 ,
,
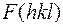 известны,
известны, 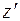 фиксировано. В ряду (16) выделяется слагаемое
фиксировано. В ряду (16) выделяется слагаемое 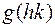 , не зависящее от
, не зависящее от 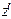
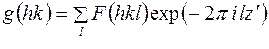 ,
,
а затем рассчитывается
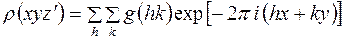 . (16)
. (16)
Разделив ячейку по оси 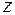 на
на 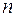 частей, можно рассчитать
частей, можно рассчитать 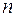 плоских сечений, а затем перейти к распределению электронной плотности в объеме элементарной ячейки. Сечения плоскостями, параллельными другим координатным плоскостям, строятся аналогичным образом.
плоских сечений, а затем перейти к распределению электронной плотности в объеме элементарной ячейки. Сечения плоскостями, параллельными другим координатным плоскостям, строятся аналогичным образом.
Можно определить сечение электронной плотности произвольной плоскостью, которая описывается уравнением:
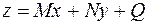 .
.
Тогда 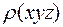 в этой плоскости рассчитывается по формуле:
в этой плоскости рассчитывается по формуле:
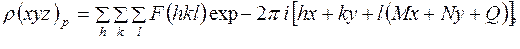
или
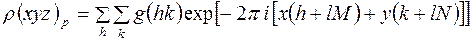 (17)
(17)
где
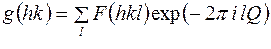 .
.
Линейные сечения определяют распределение электронной плотности вдоль прямой линии. Рассмотрим для примера сечение прямой, параллельной координатной оси z. Следовательно, необходимо найти 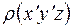 , где –
, где – 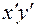 фиксированные координаты:
фиксированные координаты:
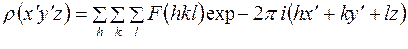 ,
,
или
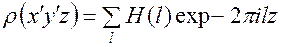 , (18)
, (18)
где
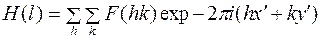 .
.
Так же как и в случае плоского сечения, получив линейные сечения, можно перейти к объемному распределению 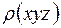 . Для этого необходимо грань
. Для этого необходимо грань 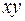 разделить на n2 частей и через точки деления провести прямые, параллельные z. Найдя распределение
разделить на n2 частей и через точки деления провести прямые, параллельные z. Найдя распределение 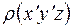 по всем линиям, проходящим через точки деления параллельно оси z, можно представить всю трехмерную структуру.
по всем линиям, проходящим через точки деления параллельно оси z, можно представить всю трехмерную структуру.
Линейное сечение можно найти для любой прямой, не обязательно параллельной координатной оси. Для этого необходимо учесть зависимость z от (ху), и в формулах (12)–(14) провести соответствующую замену z на 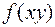 .
.
В общем случае можно получать не только плоские или линейные сечения электронной плотности. Можно отыскивать распределение электронной плотности вдоль любой поверхности (линии). Для этого необходимо просто в формуле электронной плотности учесть зависимость между координатами.
Проекции электронной плотности
Наряду с методами сечений в структурном анализе широко применяется метод проекций. Проекцией электронной плотности на плоскость в точке 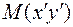 называется суммарное значение электронной плотности во всех точках элементарной ячейки, координаты которых
называется суммарное значение электронной плотности во всех точках элементарной ячейки, координаты которых  одинаковы (z, естественно, меняется от 0 до 1).
одинаковы (z, естественно, меняется от 0 до 1).
Если 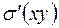 – проекция в точке
– проекция в точке 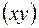 , то
, то
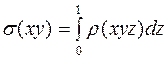 . (19)
. (19)
Выражение (19) позволяет записать рабочую формулу для определения проекций на плоскость. Учтем, что электронная плотность определяется в электронных единицах, поэтому если в процессе преобразований иногда появляются постоянные множители, мы не будем принимать их во внимание и записывать не будем.
С учетом формулы (12), получим
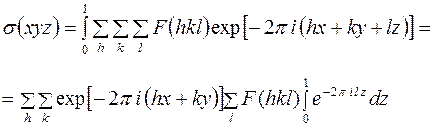 .
.
Рассмотрим
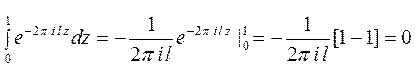 .
.
Результат несколько неожиданный. Из него следует равенство нулю величины 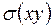 . На самом деле это не всегда так. Рассмотренный интеграл равен нулю при всех значениях индекса l¹0 и равен единице при l=0. Таким образом, проекция электронной плотности на плоскость
. На самом деле это не всегда так. Рассмотренный интеграл равен нулю при всех значениях индекса l¹0 и равен единице при l=0. Таким образом, проекция электронной плотности на плоскость 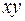 рассчитывается по формуле:
рассчитывается по формуле:
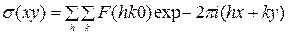 . (20)
. (20)
Следовательно, для построения проекций электронной плотности на плоскости 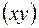 необходимо брать отражения только типа
необходимо брать отражения только типа 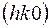 .
.
Если строится проекция на плоскость 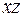 , то берутся рефлексы
, то берутся рефлексы 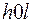 , если на плоскость
, если на плоскость 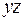 , то –
, то – 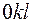 .
.
Линейная проекция электронной плотности, например, на ось 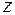
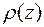 определяется следующим образом:
определяется следующим образом:
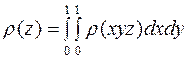 ,
,
т. е.
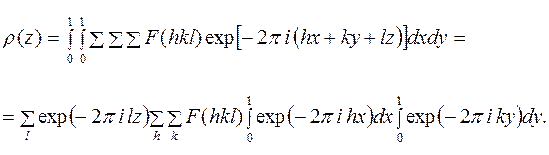
Интегралы имеют ненулевые значения только тогда, когда 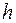 и
и 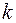 равны нулю. Следовательно,
равны нулю. Следовательно,
 . (21)
. (21)
Для построения линейных проекций электронной плотности на ось 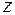 необходимо использовать базальные отражения (00l). Аналогично, для проецирования на оси
необходимо использовать базальные отражения (00l). Аналогично, для проецирования на оси 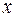 и
и 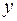 надо брать отражения типа
надо брать отражения типа 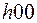 и
и 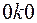 соответственно.
соответственно.
Если на элементарную ячейку приходится достаточно большое количество атомов, то при их проецировании может произойти взаимоналожение максимумов электронной плотности. Это исказит картину распределения атомов и затруднит или сделает невозможным определение их координат. В таком случае возможно использование проекции не всей элементарной ячейки, а ее части. Например, проекция электронной плотности в слое между 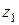 и
и 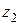 на координатную плоскость
на координатную плоскость 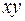 имеет вид:
имеет вид:
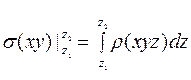 ,
,
т. е.
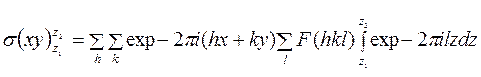 .
.
Вычислим интеграл
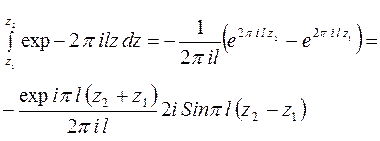 .
.
Отсюда
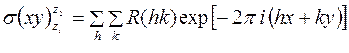 ,
,
где
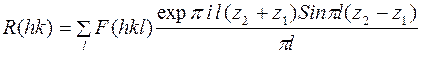 . (22)
. (22)
Анализируя проекции электронной плотности на различные координатные плоскости, можно определить все три координаты атомов, что и является решением основной задачи структурного анализа.
Рассматривая методы построения проекций и сечений  , мы убедились, что зачастую необходимо использовать не тройные (трехмерные), а двойные или даже одномерные ряды Фурье. Конечно при понижении размерности ряда расчетная работа упрощается, но, не смотря на это, остается достаточно сложной. В структурном анализе существует достаточно хорошо разработанная методика суммирования рядов Фурье, рекомендациями которой необходимо пользоваться в практической работе.
, мы убедились, что зачастую необходимо использовать не тройные (трехмерные), а двойные или даже одномерные ряды Фурье. Конечно при понижении размерности ряда расчетная работа упрощается, но, не смотря на это, остается достаточно сложной. В структурном анализе существует достаточно хорошо разработанная методика суммирования рядов Фурье, рекомендациями которой необходимо пользоваться в практической работе.
Суммирование одномерных рядов Фурье
Рассмотрим ряд (21)
 .
.
Для определения  в конкретной точке
в конкретной точке 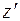 можно пользоваться формулой (21), но экспонента не очень удобная для расчета функция, поэтому на практике поступают следующим образом. Формулу (21) перепишем в виде косинус- и синус-Фурье рядов:
можно пользоваться формулой (21), но экспонента не очень удобная для расчета функция, поэтому на практике поступают следующим образом. Формулу (21) перепишем в виде косинус- и синус-Фурье рядов:
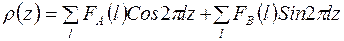 (23)
(23)
Рассмотрим ряд
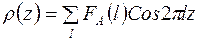 . (24)
. (24)
Элементарная ячейка (ее ребро С) делится на 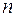 частей. Электронная плотность
частей. Электронная плотность 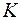 -ой точки деления определится по формуле
-ой точки деления определится по формуле
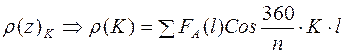 , (25)
, (25)
где 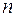 может быть любое. Выберем такое
может быть любое. Выберем такое 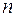 , чтобы
, чтобы 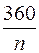 было целым числом. Например,
было целым числом. Например, 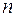 =60 или
=60 или 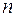 =120. Рассмотрим случай
=120. Рассмотрим случай 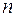 =60. В этом случае формула (23) перепишется:
=60. В этом случае формула (23) перепишется:
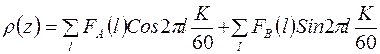 ,
,
где 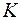 принимает значения от 0 до 60. Заранее найдем косинусы углов 0о,6о, 12о,….90о. Ясно, что никаких других значений аргументов в функции косинуса быть не может.
принимает значения от 0 до 60. Заранее найдем косинусы углов 0о,6о, 12о,….90о. Ясно, что никаких других значений аргументов в функции косинуса быть не может.
Составим таблицу по следующему образцу
Образец таблицы для расчета ряда (24)
| … | … | … | … | … |
В таблице должно быть столько строк, сколько отражений серии  мы имеем, и 31 столбец (
мы имеем, и 31 столбец ( 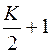 ). Вообще-то мы должны взять не 31, а 61 столбец, так как ребро С разделено на 60 частей. Но делать не нужно, так как в 31 столбце будут те же значения, что и в 29, а в 32 – то же, что в 28 и т.д. Через столбец 330 проходит плоскость симметрии. В столбец
). Вообще-то мы должны взять не 31, а 61 столбец, так как ребро С разделено на 60 частей. Но делать не нужно, так как в 31 столбце будут те же значения, что и в 29, а в 32 – то же, что в 28 и т.д. Через столбец 330 проходит плоскость симметрии. В столбец  запишем все
запишем все  . Первая строка таблицы соответствует
. Первая строка таблицы соответствует 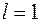 , вторая -
, вторая - 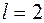 и т.д. до
и т.д. до 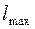 .Начнем заполнять первую строку. В столбец
.Начнем заполнять первую строку. В столбец 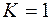 должны записать значение
должны записать значение 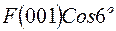 . Дальше
. Дальше 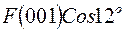 и так далее до столбца
и так далее до столбца  . В столбец
. В столбец  запишем значение
запишем значение 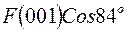 . В столбец
. В столбец 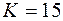 поставим 0, так как
поставим 0, так как 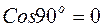 . В столбец
. В столбец 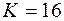 то же значение, что и в
то же значение, что и в  , но с другим знаком, ибо
, но с другим знаком, ибо 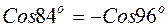 . Заполнив первую строку, переходим ко второй. Здесь будут использованы косинусы 12о, 24о, 36о. Заполняем до 14 столбца, где должно стоять значение
. Заполнив первую строку, переходим ко второй. Здесь будут использованы косинусы 12о, 24о, 36о. Заполняем до 14 столбца, где должно стоять значение 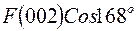 . В 15 столбец запишем значение
. В 15 столбец запишем значение 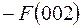 , ибо
, ибо 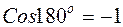 . В 16 столбец –то, что было в 14, в 17 – то, что было в 13 и т.д.
. В 16 столбец –то, что было в 14, в 17 – то, что было в 13 и т.д.
Аналогично рассчитываются следующие строчки. Везде надо считать только до 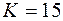 , а дальше надо переписать в 16 то, что было в 14 и т.д. Но если
, а дальше надо переписать в 16 то, что было в 14 и т.д. Но если 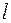 нечетное, надо менять знак, если
нечетное, надо менять знак, если 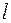 четное, то строка с
четное, то строка с 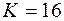 просто переписывается в обратном порядке. При этом необходимо учитывать и знаки исходных
просто переписывается в обратном порядке. При этом необходимо учитывать и знаки исходных 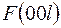 .Заполнив таблицу, необходимо просуммировать все значения по столбцам. Эта сумма и определит значение электронной плотности в точке с относительной координатой
.Заполнив таблицу, необходимо просуммировать все значения по столбцам. Эта сумма и определит значение электронной плотности в точке с относительной координатой
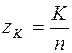 .
.
Как пример расчета одномерных косинусоидальных Фурье-рядов приведем результат определения проекции электронной плотности на ось 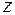 для кристаллов слюды мусковит, состав которой K(Si3Al)Al2O10(OH)2, и полученный график электронной плотности.
для кристаллов слюды мусковит, состав которой K(Si3Al)Al2O10(OH)2, и полученный график электронной плотности.
По рентгеновской дифрактограмме монокристалла определены углы дифракции 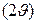 , брэгговские углы
, брэгговские углы 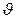 , межплоскостные расстояния
, межплоскостные расстояния 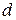 и интенсивности отражениий
и интенсивности отражениий 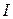 , которые заносятся в таблицу в порядке возрастания
, которые заносятся в таблицу в порядке возрастания  . Так как на рентгенограмме монокристалла фиксируются отражения (00l), а сингония слюды моноклинная, то
. Так как на рентгенограмме монокристалла фиксируются отражения (00l), а сингония слюды моноклинная, то
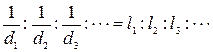 .
.
Интенсивность рентгеновского отражения 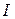 зависит от структурного фактора и фактора
зависит от структурного фактора и фактора 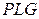 , который для метода рентгеновской дифрактометрии монокристаллов определяется по формуле:
, который для метода рентгеновской дифрактометрии монокристаллов определяется по формуле:
 .
.
Величина 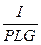 пропорциональна
пропорциональна 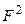 . Структура слюд такова, что ее кристаллы являются центрально-симметричными. Это означает, что
. Структура слюд такова, что ее кристаллы являются центрально-симметричными. Это означает, что 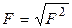 принимают действительные значения. Оставим в стороне знаковую проблему, ее решение требует специального обсуждения, которое уведет в сторону от задач данного пособия. Укажем лишь, что для слюд
принимают действительные значения. Оставим в стороне знаковую проблему, ее решение требует специального обсуждения, которое уведет в сторону от задач данного пособия. Укажем лишь, что для слюд  имеет знак «плюс» для
имеет знак «плюс» для 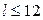 кроме значений
кроме значений 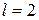 и
и 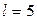 . То есть
. То есть 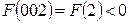 и
и 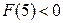 . Указанные экспериментальные и рассчитанные значения приведены в табл. 2. Заметим, что значения
. Указанные экспериментальные и рассчитанные значения приведены в табл. 2. Заметим, что значения 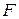 увеличены в 10 раз и округлены до целых чисел. Это сделано для удобства расчетов.
увеличены в 10 раз и округлены до целых чисел. Это сделано для удобства расчетов.
Таблица 2
Расчет структурных амплитуд  кристаллов мусковита,
кристаллов мусковита,
полученных на основе рентгендифрактометрических исследований
| № | 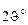
| 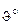
| 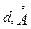
| 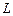
| 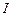 , мм , мм
| 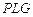
| 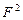
| 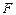
|
| 9,00 17,83 26,90 | 4,50 8,82 13,45 | 9,92 4,97 3,31 | 24,2 24,4 46,6 | 12,63 6,23 3,97 | 1,92 3,92 11,74 | -20 | ||
| 36,00 45,50 55,25 | 18,00 22,75 27,63 | 2,49 1,99 1,66 | 7,0 18,2 0,6 | 2,81 2,10 1,61 | 2,49 8,70 0,37 | -29 | ||
| 65,50 78,25 88,00 | 32,75 39,13 44,00 | 1,42 1,24 1,11 | 2,7 3,9 0,2 | 1,29 1,09 1,00 | 2,10 3,59 0,20 | |||
| 101,00 116,25 137,75 | 50,50 58,13 67,88 | 0,998 0,907 0,8315 | 1,5 2,2 1,3 | 1,06 1,33 2,16 | 1,18 1,05 0,57 |
Суммирование рядов проводится на компьютере, но мы решили привести все промежуточные значения 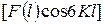 для
для 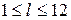 и
и 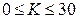 (табл. 3). Приведенные в табл. 3 результаты позволяют увидеть периодичность распределения этих величин в зависимости от
(табл. 3). Приведенные в табл. 3 результаты позволяют увидеть периодичность распределения этих величин в зависимости от 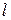 и
и 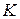 . Прежде чем описывать связь между функцией
. Прежде чем описывать связь между функцией 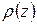 и распределением атомов в слюде, рассмотрим структуру этого кристалла. Слюды – типичные представители слоистых силикатов, характеризуются различными составами с общей кристаллохимической формулой:
и распределением атомов в слюде, рассмотрим структуру этого кристалла. Слюды – типичные представители слоистых силикатов, характеризуются различными составами с общей кристаллохимической формулой:
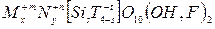 ,
,
где 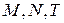 – межслоевой, октаэдрический и тетраэдрический атомы соответственно. Верхний индекс в формуле – валентность, нижний – число атомов. При этом должны выполняться условия:
– межслоевой, октаэдрический и тетраэдрический атомы соответственно. Верхний индекс в формуле – валентность, нижний – число атомов. При этом должны выполняться условия: 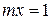 ,
, 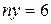 , что обеспечивает электростатическую нейтральность ячейки кристалла слюды.
, что обеспечивает электростатическую нейтральность ячейки кристалла слюды. 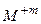 – атомыK+1, Na+1, Li+1, Ca+2, N+n-Fe+2, Mg+2, Mn+2, Al+3, Fe+3, Ti+4,
– атомыK+1, Na+1, Li+1, Ca+2, N+n-Fe+2, Mg+2, Mn+2, Al+3, Fe+3, Ti+4,
T-Al+3. Возможны вхождения в структуру не только комбинаций этих, но и некоторых других атомов. Атомы в кристаллах слюд расположены по слоям, как это показано на рис.
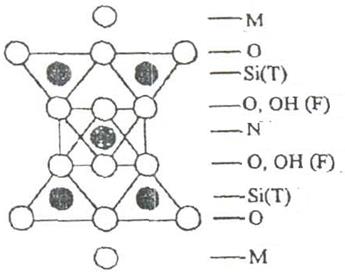
Рис. 1. Схема последовательности атомных слоев в слюдах
Если в кристаллической формуле 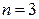 , то в октаэдрическом слое заняты две из трех октаэдрических позиций, если
, то в октаэдрическом слое заняты две из трех октаэдрических позиций, если 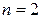 – то все позиции, т. е. три из трех. Слюды первого типа называются диоктаэдрическими, второго – триоктаэдрическими. Мусковит – K(Si3Al)Al2O10(OH)2 – является типичным представителем диоктаэдрических, флогопит K(Si3Al)Mg3O10(OH)2 и биотит K(Si3Al)Fe3O10(OH)2 – триоктаэдрических слюд. Полиэдрические модели ди- и триоктаэдрических слюд приведены на рис. 2.
– то все позиции, т. е. три из трех. Слюды первого типа называются диоктаэдрическими, второго – триоктаэдрическими. Мусковит – K(Si3Al)Al2O10(OH)2 – является типичным представителем диоктаэдрических, флогопит K(Si3Al)Mg3O10(OH)2 и биотит K(Si3Al)Fe3O10(OH)2 – триоктаэдрических слюд. Полиэдрические модели ди- и триоктаэдрических слюд приведены на рис. 2.
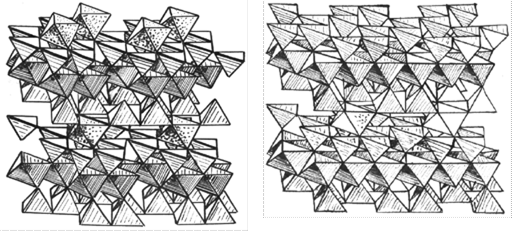
Рис. 37. Полиэдрическая модель ди- (а) и триоктаэдрических (б) слюд
Таблица 3
Расчет проекций электронной плотности 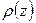 кристалла мусковита
кристалла мусковита
| l | K | |||||||||||||||||||||
| -20 -29 | 13,92 -19,56 32,33 14,61 -25,11 4,85 10,40 12,72 2,35 5,51 5,29 2,17 | 13,69 -18,27 27,51 10,71 -14,51 1,86 1,47 -1,97 -1,23 -5,49 -8,69 -5,66 | 13,31 -16,18 20,00 4,95 -0,02 -1,85 -8,22 -15,36 -3,80 -11,00 -12,37 -5,67 | 12,79 -13,39 10,53 -1,66 14,47 -4,85 -13,69 -18,59 -3,24 -5,52 -1,39 2,15 | 12,13 -10,01 0,03 -7,98 25,09 -6,00 -12,14 -9,53 -0,01 5,47 11,24 7,00 | 11,33 -6,19 -10,48 -12,93 29,00 -4,86 -4,36 5,82 3,23 11,00 10,54 2,19 | 10,41 -2,10 -19,95 -15,64 25,14 -1,87 5,66 17,33 3,81 5,53 -2,65 -5,64 | 9,37 2,07 -27,48 -15,66 14,55 1,84 12,77 17,38 1,25 -5,46 -12,70 -5,68 | 8,23 6,16 -32,32 -12,96 0,07 4,84 13,33 5,94 -2,34 -11,00 -7,70 2,12 | 7,01 9,98 -34,00 -8,03 -14,43 6,00 7,04 -9,43 -4,00 -5,55 6,43 7,00 | ||||||||||||
| S | 59,49 | -0,57 | -36,21 | -22,39 | 15,29 | 34,29 | 20,02 | -7,74 | -25,61 | -31,98 | ||||||||||||
| 5,70 13,36 -32,35 -1,71 -25,07 4,87 -2,85 -18,57 -2,37 5,44 12,94 2,21 | 4,33 16,16 -27,54 4,90 -29,00 1,88 -11,29 -15,43 1,21 11,00 4,10 -5,63 | 2,92 18,26 -20,04 10,67 -25,16 -1,83 -13,93 -2,09 3,80 5,57 -9,59 -5,70 | 1,47 19,56 -10,58 14,60 -14,59 -4,84 -9,42 12,63 3,25 -5,43 -11,92 2,10 | 0,01 20,00 -0,08 16,00 -0,11 -6,00 -0,08 19,00 0,03 -11,00 -0,11 7,00 | -1,45 19,57 10,42 14,64 14,39 -4,87 9,31 12,81 -3,22 -5,58 11,83 2,23 | -2,90 18,28 19,91 10,75 25,05 -1,88 13,91 -1,85 -3,81 5,41 9,75 -5,62 | -4,31 16,20 27,45 5,00 29,00 1,82 11,38 -15,29 -1,27 11,00 -3,89 -5,71 | -5,68 13,41 32,30 -1,61 25,19 4,83 3,01 -18,62 2,32 5,60 -12,91 2,08 | -6,99 10,04 34,00 -7,94 14,63 6,00 -6,91 -9,64 4,00 -5,40 -6,63 7,00 | |||||||||||||
| S | -38,40 | -45,29 | -37,13 | -3,17 | 44,65 | 80,08 | 87,00 | 71,39 | 49,92 | 32,16 | ||||||||||||
| -8,22 6,22 32,37 -12,90 0,16 4,88 -13,28 5,71 2,38 -11,00 7,51 2,25 | -9,36 2,14 27,58 -15,63 -14,35 1,89 -12,84 17,28 -1,20 -5,61 12,75 -5,60 | -10,39 -2,04 20,08 -15,67 -25,03 -1,81 -5,80 17,43 -3,79 5,38 2,87 -5,72 | -11,32 -6,13 10,63 -12,99 -29,00 -4,83 4,21 6,05 -3,26 11,00 -10,41 2,06 | -12,11 -9,95 0,13 -8,07 -25,21 -6,00 12,06 -9,32 -0,05 5,63 -11,35 7,00 | -12,78 -13,34 -10,37 -1,76 -14,67 -4,88 13,72 -18,54 3,21 -5,37 1,16 2,27 | -13,31 -16,15 -19,87 4,86 -0,21 -1,90 8,34 -15,50 3,82 -11,00 12,30 -5,59 | -13,69 -18,25 -27,42 10,63 14,31 1,80 -1,32 -2,21 1,29 -5,64 8,85 -5,74 | -13,92 -19,55 -32,29 14,58 25,00 4,82 -10,30 12,54 -2,31 5,35 -5,09 2,04 | -14,00 -20,00 -34,00 16,00 29,00 6,00 -14,00 19,00 -4,00 11,00 -13,00 7,00 | |||||||||||||
| S | 16,09 | -2,95 | -24,48 | -43,98 | -57,26 | -61,36 | -54,20 | -37,37 | -19,12 | -11,00 | ||||||||||||
Основу структуры слюд составляет двойной кремнекислородный пакет, состоящий из двух тетраэдрических слоев плотнейшей упаковки, соединяющихся промежуточной октаэдрической сеткой атомов двух- и трехвалентных металлов. Заряд такого пакета при соотношении слоев 2:1, равный -1, компенсируется межслоевым положительным катионом.
Кривая функции 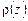 , расчет которой приведен в табл. 3, представлена на рис. 3, под которым приведен фрагмент структуры – половина ячейки – по оси z (см. рис. 1 и рис. 2).
, расчет которой приведен в табл. 3, представлена на рис. 3, под которым приведен фрагмент структуры – половина ячейки – по оси z (см. рис. 1 и рис. 2).
Из рис. 38 следуют два важных, на наш взгляд, следствия. Во-первых, само численное значение электронной плотности носит относительный характер, так как на отдельных участках электронная плотность отрицательная, что не имеет физического смысла. Обусловлено это тем, что 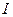 и, следовательно,
и, следовательно, 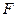 измерены в произвольных единицах. Переход к другим единицам измерения интенсивности отражений на положение максимумов функции
измерены в произвольных единицах. Переход к другим единицам измерения интенсивности отражений на положение максимумов функции  не отразится, а повлияет лишь на нулевое положение
не отразится, а повлияет лишь на нулевое положение  .
.
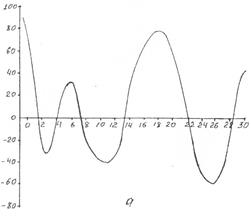
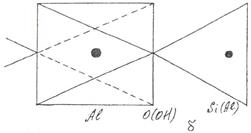

Рис. 3. а) проекция электронной плотности на ось z мусковита;
б) фрагмент структуры кристалла мусковита
Во-вторых, на практике приходится решать задачу, связанную с построением структурной модели по распределению электронной плотности, что, конечно, намного сложнее, чем отождествление максимумов 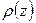 с атомами известной структуры кристалла. Здесь приведена лишь иллюстрация метода построения
с атомами известной структуры кристалла. Здесь приведена лишь иллюстрация метода построения 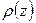 для таких природных неорганических кристаллических сложных полимеров как слюды, типичным представителем которых и является мусковит.
для таких природных неорганических кристаллических сложных полимеров как слюды, типичным представителем которых и является мусковит.
Суммирование двумерных трехмерных рядов Фурье
Двумерный экспоненциальный ряд Фурье преобразуем, выделив действительную и мнимую части структурной амплитуды:
 ,
,
Получаются двумерные ряды типа
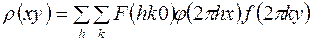 ,
,
где 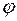 и
и 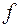 функции косинуса или синуса.
функции косинуса или синуса.
Рассмотрим, например, косинус-косинус ряд Фурье.
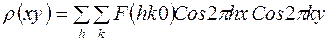 .
.
Разбивая ячейку на 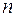 частей, получаем
частей, получаем 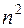 точек. Будем идти по рядам. Выбираем первый ряд. Для него фиксированы значения (
точек. Будем идти по рядам. Выбираем первый ряд. Для него фиксированы значения ( 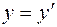 )
)
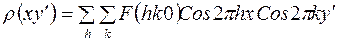 ,
,
или 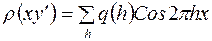 ,
,
где 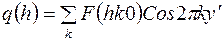 . (25)
. (25)
Фиксируя h, получим одномерный ряд, в котором коэффициентами являются величины 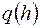 .
.
Итак, суммирование двумерных косинус-косинус рядов Фурье осуществляется следующим образом.
Вначале ищем электронную плотность вдоль линии 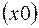 по формуле
по формуле
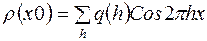 ,
,
где 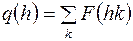 ,
,
т.е. 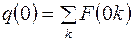
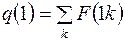 .
.
Затем координата у меняется на  ,
,
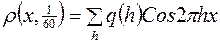 ,
,
но 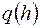 теперь ищем по формулам
теперь ищем по формулам
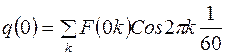 ,
,
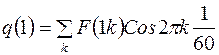 и т.д.
и т.д.
Двумерные косинус-синус, синус- косинус и синус-синус Фурье ряды суммируются по аналогичной схеме. Просуммировать тригонометрические ряды, можно переходить к расчету экспоненциального Фурье-ряда.
Рассмотрим теперь методы суммирования трехмерного ряда Фурье, который в самом общем случае записывается в формуле:
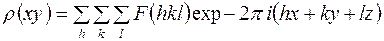 .
.
Этот трехмерный экспоненциальный ряд преобразуем в трехмерные тригонометрические ряды Фурье. Рассмотрим один из членов ряда:
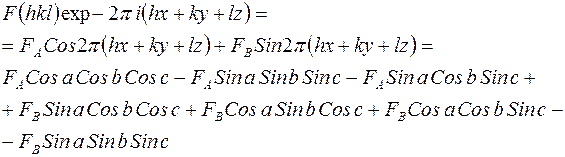 ,
,
где 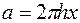 ,
, 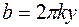 ,
, 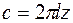 ,
,
т.е. трехмерный экспоненциальный ряд Фурье можно представить в форме тригонометрических рядов следующего вида:
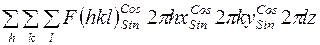 . (28)
. (28)
Методы суммирования таких рядов рассмотрим на примере ряда
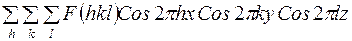 . (29)
. (29)
Сначала найдем распределение электронной плотности в плоскости, параллельной координатной  , т.е. зафиксируем координату
, т.е. зафиксируем координату  , т.е рассчитаем
, т.е рассчитаем
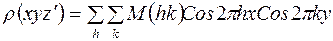 ,
,
где
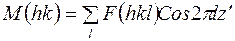 , (30)
, (30)
т.е.
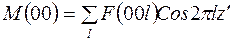
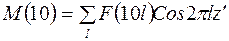 .
.
Рассчитав 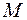 для различных
для различных 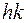 , можно найти распределение электронной плотности в плоскости, параллельной
, можно найти распределение электронной плотности в плоскости, параллельной 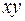 , лежащей на высоте
, лежащей на высоте 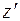 . Затем переходим к следующей плоскости с координатой
. Затем переходим к следующей плоскости с координатой 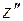 и т.д.
и т.д.
Суммирование трехмерных рядов, таким образом, предполагает построение плоских сечений, распределение в которых определяется двумерным двумерным рядом (30), а методика их суммирования изложена выше.
Для суммирования трехмерных рядов можно использовать аналогию не только с плоским сечением, но и с сечением линейным. Зафиксируем координаты 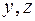 :
: 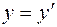 ,
, 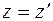 , т.е. найдем распределение электронной плотности вдоль линии, параллельной оси
, т.е. найдем распределение электронной плотности вдоль линии, параллельной оси 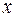
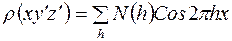 , (31)
, (31)
где 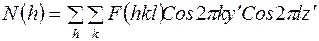 ,
,
т.е. 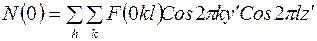
или 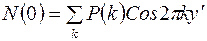 ,
,
где 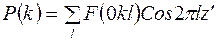 .
.
Суммирование двух и трехмерных рядов требуеточень большой расчетной работы, поэтому для расчета 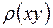 и
и 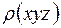 необходимо использовать ПЭВМ.
необходимо использовать ПЭВМ.
Метод Фурье - аналитический метод расчета кристаллических структур – сожжет быть использован только в том случае, если известны фазы (или знаки) структурных амплитуд. Определение фаз или знаков структурных амплитуд – достаточно трудная проблема, которая мешает широкому использованию метода Фурье. Обойти фазовую проблему в какой-то степени можно, используя метод проб и ошибок, но существует и другой способ, который также не требует решения фазовой (знаковой) проблемы, когда в качестве исходных данных используются не структурные амплитуды, а значения структурных факторов, значения которых определяются непосредственно из эксперимента. Этот метод по имени предложившего его автора называется методом Паттерсона.
Метод Паттерсона
Если построить ряд Фурье, коэффициентами которого являются структурные амплитуды, то можно найти распределение электронной плотности, максимумы которой соответствуют центрам атомов. Наряду с функцией электронной плотности можно ввести и другие функции, связанные с 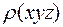 , которые вполне определенным образом зависят от координат атомов в кристалле.
, которые вполне определенным образом зависят от координат атомов в кристалле.
В качестве такой функции можно брать так называемую функцию межатомных векторов (или межатомную функцию, или функцию Паттерсона).
Понятие межатомного вектора, вероятно, не нуждается в пояснении. Отметим, все же, что межатомный вектор абсолютно однозначно описывает положение двух атомов относительно друг друга. В этом смысле он несет вполне конкретную информацию о структуре объекта. Если задан межатомный вектор 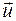 , то в структуре на расстоянии от одного из атомов, равном модулю
, то в структуре на расстоянии от одного из атомов, равном модулю 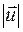 , и в направлении, заданном этим вектором, расположен другой атом. Итак, если есть межатомный вектор
, и в направлении, заданном этим вектором, расположен другой атом. Итак, если есть межатомный вектор 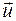 с проекциями на координатные оси
с проекциями на координатные оси 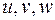 , то назовем межатомной функцией
, то назовем межатомной функцией 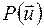 следующее выражение
следующее выражение
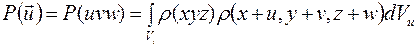 (1)
(1)
Межатомная функция определяет среднее произведение электронной плотности на концах вектора 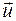 .
.
Исходя из определения (1) можно найти выражение 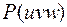 через
через 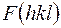 , так как
, так как
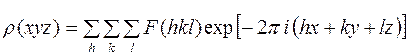
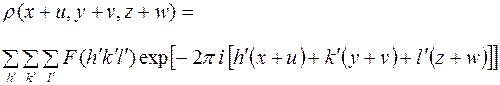 . (2)
. (2)
Индексы суммирования  и
и 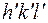 не обязательно должны быть одинаковыми, ибо
не обязательно должны быть одинаковыми, ибо 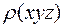 и
и 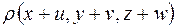 определяются независимо.
определяются независимо.
Итак,
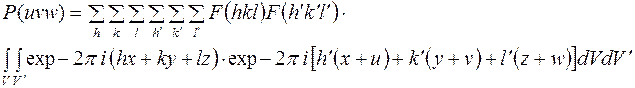 (3)
(3)
Рассмотрим один из интегралов
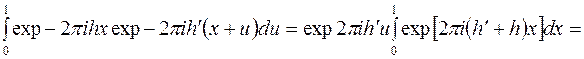
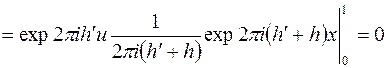
так как 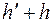 - целое число.
- целое число.
Но если 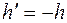 , то интеграл
, то интеграл
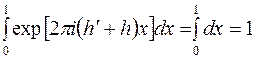
т.е. из бесчисленного множества сочетаний 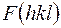 и
и 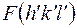 ненулевой вклад в значение
ненулевой вклад в значение 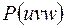 дадут только те пары индексов, которые связаны условием
дадут только те пары индексов, которые связаны условием 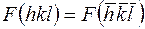 . Но
. Но
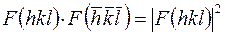 .
.
Отсюда, опуская штрихи 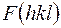 , получим
, получим
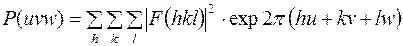 . (4)
. (4)
Следовательно, функция Паттерсона является трансформантой Фурье структурного фактора 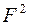 . Формула (4) не является окончательным выражением межатомной функции. Учтем, что для любой пары атомов А и В всегда
. Формула (4) не является окончательным выражением межатомной функции. Учтем, что для любой пары атомов А и В всегда 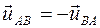 . В соответствие с формулой Эйлера (с точностью до постоянного множителя) функция
. В соответствие с формулой Эйлера (с точностью до постоянного множителя) функция 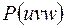 запишется
запишется
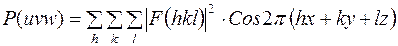 . (5)
. (5)
Для того, чтобы подробнее говорить о применимости межатомной функции для описания структур кристаллов, рассмотрим связь между распределением атомов в кристалле и изображением этого распределения в векторном пространстве.
Межатомные векторы можно изобразить в специально выбранной системе координат точками, радиусы векторы которых равны этим межатомным векторам. Совокупность таких точек определит векторную систему кристалла.
Каждой точке векторного пространства мы можем приписать не только три координаты, но и ее «вес» численно равный 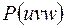 по аналогии с функцией
по аналогии с функцией 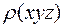 в пространстве кристалла.
в пространстве кристалла.
Переход от пространства кристалла к векторному пространству
С практической точки зрения переход от пространства кристалла к векторному не представляет большого интереса, ибо если известна структура кристалла, то значит основная задача структурного анализа решена, и, кроме того распределение функции Паттерсона легко найти из эксперимента, т.к. в формуле для расчета 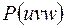 фигурирует только
фигурирует только 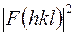 . Считаем, что рентгенограмма проиндицирована. Мы осуществляем переход от пространства кристалла к векторному пространству для того, чтобы отыскать некоторые закономерности, облегчающие наиболее важный в практическом отношении переход от векторного к пространству кристалла.
. Считаем, что рентгенограмма проиндицирована. Мы осуществляем переход от пространства кристалла к векторному пространству для того, чтобы отыскать некоторые закономерности, облегчающие наиболее важный в практическом отношении переход от векторного к пространству кристалла.
Генерация страницы за: 0.221 сек.
