Парная регрессия и корреляция 4 страница
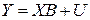 .
.
Для вычисления коэффициентов уравнения регрессии составим сумму квадратов отклонений:
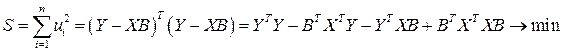 .
.
Так как 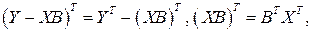
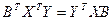 , то
, то
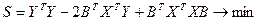 .
.
Необходимым условием экстремума служит обращение в нуль частных производных функции S по параметрам. Дифференцируя S по B, получаем
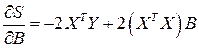 .
.
Приравнивая 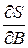 нулю, находим систему нормальных уравнений, которая в матричной форме имеет вид
нулю, находим систему нормальных уравнений, которая в матричной форме имеет вид
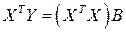 .
.
Решение полученной системы определяется по формуле
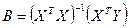 . (2.3)
. (2.3)
Оценку параметров уравнения регрессии, найденную по формуле (2.3), называют оценкой метода наименьших квадратов.
В уравнении (2.3) матрицы 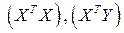 записываются в следующем виде:
записываются в следующем виде:
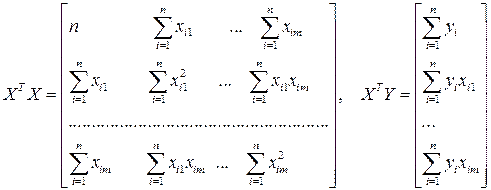 .
.
Рассмотрим процедуру построения множественной регрессии с двумя независимыми переменными, не прибегая к обращению матрицы 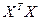 . Функция линейной множественной регрессии в этом случае имеет вид
. Функция линейной множественной регрессии в этом случае имеет вид
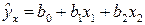 . (2.4)
. (2.4)
Сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии, должна быть минимальна:
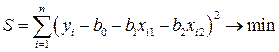 .
.
Продифференцировав S по каждому из параметров  , приравняв частные производные нулю и выполнив элементарные преобразования, получаем следующую систему нормальных уравнений:
, приравняв частные производные нулю и выполнив элементарные преобразования, получаем следующую систему нормальных уравнений:
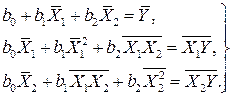 (2.5)
(2.5)
Из первого уравнения системы найдем 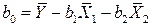 и, подставив в (2.4), получим уравнение регрессии
и, подставив в (2.4), получим уравнение регрессии
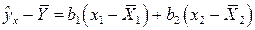 .
.
Продолжив решение системы (2.5), найдем параметры 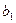 и
и 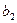 уравнения регрессии (2.4) по формулам:
уравнения регрессии (2.4) по формулам:
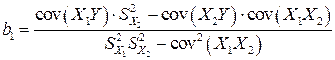 ,
,
(2.6)
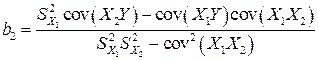 ,
,
где
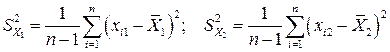 ;
;

2.2. Многофакторная линейная регрессионная модель в нормированной размерности. В случае множественной регрессии более чем с двумя независимыми переменными выполняют нормирование переменных по формулам:
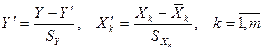 , (2.7)
, (2.7)
где 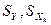 – стандартные отклонения переменных Y и
– стандартные отклонения переменных Y и 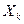 .
.
Проведенное нормирование позволяет упрощать расчеты определений оценок неизвестных параметров, так как исключается свободный член 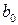 и за начало отсчета каждой переменной принимается значение среднего, а за единицу измерения – значение стандартного отклонения. Уравнение множественной линейной регрессии в нормированной размерности приобретает вид
и за начало отсчета каждой переменной принимается значение среднего, а за единицу измерения – значение стандартного отклонения. Уравнение множественной линейной регрессии в нормированной размерности приобретает вид
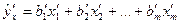 , (2.8)
, (2.8)
где 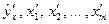 – значения нормированных переменных;
– значения нормированных переменных; 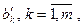 – нормированные коэффициенты регрессии.
– нормированные коэффициенты регрессии.
Оценки 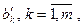 нормированных коэффициентов множественной регрессии находим методом наименьших квадратов. Из соответствующих формул следуют соотношения между обычными и нормированными коэффициентами регрессии
нормированных коэффициентов множественной регрессии находим методом наименьших квадратов. Из соответствующих формул следуют соотношения между обычными и нормированными коэффициентами регрессии 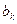 и
и 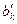 :
:
 . (2.9)
. (2.9)
Как отмечалось выше, коэффициенты регрессии 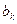 имеют размерность переменной Y, деленную на размерность переменной
имеют размерность переменной Y, деленную на размерность переменной 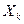 . Поэтому любое изменение единицы переменной величины сказывается на коэффициенте регрессии. Из формул (2.7 и (2.8) следует, что нормированные переменные
. Поэтому любое изменение единицы переменной величины сказывается на коэффициенте регрессии. Из формул (2.7 и (2.8) следует, что нормированные переменные 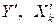 и нормированные коэффициенты регрессии
и нормированные коэффициенты регрессии 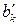 безразмерны. Вследствие этого становится возможным сравнение факторных переменных при оценке интенсивности их влияния на результативный признак, так как нормированные переменные выражаются в единицах стандартных отклонений.
безразмерны. Вследствие этого становится возможным сравнение факторных переменных при оценке интенсивности их влияния на результативный признак, так как нормированные переменные выражаются в единицах стандартных отклонений.
Нормированные коэффициенты множественной регрессии характеризуют скорость изменения среднего значения результативного признака 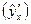 по каждому факторному признаку
по каждому факторному признаку 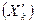 при постоянных значениях остальных факторов, включенных в модель. Они показывают, на какую часть стандартного отклонения изменилось бы среднее значение результативного признака, если бы значение факторного признака увеличилось на стандартное отклонение, а прочие факторы остались без изменения.
при постоянных значениях остальных факторов, включенных в модель. Они показывают, на какую часть стандартного отклонения изменилось бы среднее значение результативного признака, если бы значение факторного признака увеличилось на стандартное отклонение, а прочие факторы остались без изменения.
Таким образом, нормированные коэффициенты регрессии показывают сравнительную силу влияния каждого фактора-признака на изменение результативного признака.
2.3. Линейная частная регрессия. Из приведенных выше рассуждений следует, что в множественной регрессии исследуется одновременное влияние нескольких 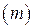 факторных признаков
факторных признаков 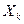 на результативный признак Y. При этом указывалось, что коэффициент множественной регрессии
на результативный признак Y. При этом указывалось, что коэффициент множественной регрессии 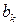 выражает частное влияние фактора
выражает частное влияние фактора 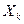 на результативный признак Y при постоянных значениях других факторов. Это означает, что между множественной и частной регрессиями нет разницы. Покажем это для трех связанных между собой переменных Y,
на результативный признак Y при постоянных значениях других факторов. Это означает, что между множественной и частной регрессиями нет разницы. Покажем это для трех связанных между собой переменных Y, 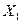 и
и  . Предположим, что между переменными
. Предположим, что между переменными 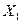 ,
,  и Y существуют линейные соотношения. Представим частную регрессию Y на
и Y существуют линейные соотношения. Представим частную регрессию Y на 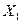 при исключении
при исключении  . Для этого вначале найдем простые регрессии Y на
. Для этого вначале найдем простые регрессии Y на  и
и 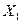 на
на  . Они выразятся следующими уравнениями:
. Они выразятся следующими уравнениями:
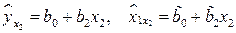 .
.
Из систем нормальных уравнений для указанных регрессий можно найти 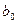 и
и 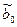 :
:
 .
.
Тогда уравнения регрессий выразятся формулами:
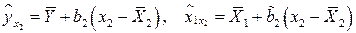 .
.
Предположим теперь, что переменная  изъята из анализа. В этом случае регрессия Y на
изъята из анализа. В этом случае регрессия Y на 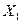 определяется по данным
определяется по данным 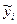 и
и 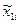 , из которых исключено влияние
, из которых исключено влияние  :
:
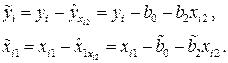
Так как средние арифметические переменных 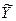 и
и 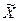 равны нулю, то уравнение регрессии по данным, из которых исключено влияние
равны нулю, то уравнение регрессии по данным, из которых исключено влияние  , имеет вид:
, имеет вид: 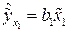 .
.
Регрессия переменных с исключением влияния  определяется коэффициентом
определяется коэффициентом 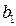 , называемым коэффициентом частной регрессии. Применив метод наименьших квадратов для нахождения оценки неизвестного параметра
, называемым коэффициентом частной регрессии. Применив метод наименьших квадратов для нахождения оценки неизвестного параметра 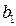 , получим
, получим
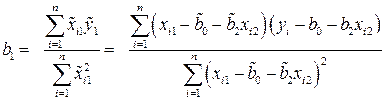 .
.
Выполняя в приведенной формуле ряд алгебраических операций, приходим к выражению, аналогичному (2.6). Этот факт подтверждает, что частная регрессия не приводит к новым результатам при исследовании зависимостей.
Итак, при изучении регрессии нет необходимости различать частную и множественную регрессии, так как коэффициенты частной регрессии совпадают с соответствующими коэффициентами множественной регрессии.
2.4.Отбор важнейших факторов многофакторных регрессионных моделей. Проблема выбора существенных переменных (факторов) для включения их в модель тесно связана с исходными предпосылками регрессионного анализа. При построении модели два момента вступают в противоречие. В модель должны войти все переменные, которые с экономической точки зрения оказывают влияние на зависимую переменную. Но большое количество переменных, включенных в модель, требует большого числа наблюдений. Невыполнение первого требования может привести к неадекватности модели из-за того, что не учтены некоторые существенные факторы, а также к нарушению нормальности распределения случайной компоненты 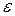 из-за того, что ее вариация будет обусловлена не только случайными факторами, но и систематически действующими, т.е. к нарушению гомоскедастичности. Дж. У. Юл и М. Дж. Кендалл считают, что максимальное число переменных, включенных в модель, не должно превышать десяти.
из-за того, что ее вариация будет обусловлена не только случайными факторами, но и систематически действующими, т.е. к нарушению гомоскедастичности. Дж. У. Юл и М. Дж. Кендалл считают, что максимальное число переменных, включенных в модель, не должно превышать десяти.
Сокращение числа переменных, входящих в модель, можно производить путем отсеивания менее существенных факторов в процессе построения регрессионной модели или путем замены исходного набора переменных меньшим числом эквивалентных переменных, полученных в результате преобразований исходного набора.
Процедура отсева несущественных факторов в процессе построения регрессионной модели называется многошаговым регрессионным анализом. Этот метод основан на построении нескольких промежуточных уравнений регрессии, в результате анализа которых получается конечная модель, включающая только факторы, оказывающие существенное влияние на исследуемый показатель. При этом выделяется три подхода.
1. Строится уравнение регрессии по максимально возможному количеству факторов, предположительно оказавших влияние на исследуемый показатель. Затем с помощью t - критерия исключаются несущественные факторы.
2. Строится парная регрессия по одному значимому фактору, а затем в уравнение регрессии последовательно вводятся по одному все значимые факторы. Этот метод называет методом пошаговой регрессии.
3. Строится несколько уравнений регрессии, затем с помощью определенного критерия выбирается наилучшее.
Кратко охарактеризуем эти методы построения регрессионных моделей.
Применение t-критерия для отбора существенных факторовосновано на предположении о нормальном распределении остатков U. Если это условие выполняется, то величина 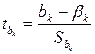
 распределена по закону Стьюдента с
распределена по закону Стьюдента с  степенями свободы. Задавая уровень значимости
степенями свободы. Задавая уровень значимости 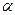 по числу степеней свободы
по числу степеней свободы 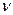 , находят квантиль t-распределения, с которым сравнивают
, находят квантиль t-распределения, с которым сравнивают 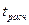 . При
. При 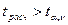 , коэффициент регрессии признается статистически значимым с вероятностью
, коэффициент регрессии признается статистически значимым с вероятностью 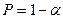 . Если все коэффициенты регрессии признаны значимыми, то уравнение регрессии считается окончательным и при общей проверке его адекватности по F-критерию принимается в качестве модели исследуемого экономического процесса. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие факторы следует исключить из уравнения регрессии, предварительно проранжировав коэффициенты регрессии по значению
. Если все коэффициенты регрессии признаны значимыми, то уравнение регрессии считается окончательным и при общей проверке его адекватности по F-критерию принимается в качестве модели исследуемого экономического процесса. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие факторы следует исключить из уравнения регрессии, предварительно проранжировав коэффициенты регрессии по значению 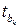 . В первую очередь исключается фактор, для которого значение
. В первую очередь исключается фактор, для которого значение 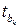 наименьшее. Исключив один фактор с наименьшим значением
наименьшее. Исключив один фактор с наименьшим значением 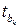 , строят уравнение регрессии без исключенного фактора и снова производят оценку коэффициентов регрессии по t-критерию. Изложенную процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми. При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводят экономический анализ несущественных факторов и устанавливают порядок их исключения. В некоторых случаях, исходя из профессиональных соображений, оставляют фактор, для которого
, строят уравнение регрессии без исключенного фактора и снова производят оценку коэффициентов регрессии по t-критерию. Изложенную процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми. При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводят экономический анализ несущественных факторов и устанавливают порядок их исключения. В некоторых случаях, исходя из профессиональных соображений, оставляют фактор, для которого 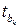 незначительно меньше
незначительно меньше 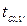 .
.
Отметим, что не существенность коэффициента регрессии по t-критерию не всегда является основанием для исключения фактора из дальнейшего анализа. Т. Андерсон рекомендовал исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратичная ошибка коэффициента регрессии превышает абсолютную величину вычисленного коэффициента, т.е. в случае, если значение t-критерия меньше единицы. При этом предполагается, что нет веских оснований для того, чтобы оставить переменную в модели. При пошаговом построении уравнения регрессии выбирают фактор 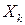 имеющий наибольший коэффициент парной корреляции с Y, и строят уравнение парной регрессии. Затем находят частныекоэффициенты корреляции между Y иостальными переменными приисключении выбранной переменной
имеющий наибольший коэффициент парной корреляции с Y, и строят уравнение парной регрессии. Затем находят частныекоэффициенты корреляции между Y иостальными переменными приисключении выбранной переменной 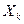 . Переменную с максимальным значением частного коэффициента корреляции включают в уравнение регрессии и вычисляют
. Переменную с максимальным значением частного коэффициента корреляции включают в уравнение регрессии и вычисляют 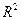 и частный F-критерий, который показывает, существенный ли вклад вносит в уравнение эта переменная по сравнению с уже введенными. Указанная процедура проводится до тех пор, пока расчетное значение F-критерия становится меньше табличного. Подчеркнем, что на каждом шаге с добавлением новой переменной определяется значимость не только новой переменной, но и переменных, уже включенных в модель. И если какие-то из них окажутся незначимыми, они исключаются из уравнения. Значимость определяется значением частного F-критерия для всех переменных модели.
и частный F-критерий, который показывает, существенный ли вклад вносит в уравнение эта переменная по сравнению с уже введенными. Указанная процедура проводится до тех пор, пока расчетное значение F-критерия становится меньше табличного. Подчеркнем, что на каждом шаге с добавлением новой переменной определяется значимость не только новой переменной, но и переменных, уже включенных в модель. И если какие-то из них окажутся незначимыми, они исключаются из уравнения. Значимость определяется значением частного F-критерия для всех переменных модели.
В многошаговом регрессионном анализе, основанном на методе случайного поиска с адаптацией, разработанным Г.С. Лбовым, применяют «поощрение» или «наказание» отдельных переменных исходя из их «ценности». В качестве критерию «ценности» используют коэффициент множественной корреляции R.
В начале поиска задают равные вероятности 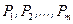 для каждого из факторов. Затем случайным образом выбирают q групп по к факторов и в этой системе определяют max R и min R. Векторы факторов в первой системе
для каждого из факторов. Затем случайным образом выбирают q групп по к факторов и в этой системе определяют max R и min R. Векторы факторов в первой системе 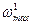 и
и 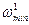 запоминают. Вероятность попадания в систему
запоминают. Вероятность попадания в систему 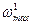 увеличивается, а в
увеличивается, а в 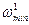 уменьшается на h (h - произвольное число). Так образовывают l систем по q групп в каждой. За эффективную принимают ту группу, при которой
уменьшается на h (h - произвольное число). Так образовывают l систем по q групп в каждой. За эффективную принимают ту группу, при которой
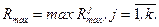
При переборе ряда групп вероятность выбора факторов, часто встречающихся в удачных сочетаниях, становится большей, и именно этот набор факторов повторяется гораздо чаще остальных. Число q выбираюттак, чтобы между значениями 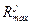 и
и 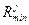 данной системы j была заключена основная часть сочетаний, а величину шага h - такой, чтобы вероятность выбора фактора, если он будетвстречаться на каждом этапе, оставалась большей или равной установленной вероятности
данной системы j была заключена основная часть сочетаний, а величину шага h - такой, чтобы вероятность выбора фактора, если он будетвстречаться на каждом этапе, оставалась большей или равной установленной вероятности 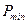 . При увеличении шага растет и доля случаев, когда эффективное сочетание факторов не будет найдено. При
. При увеличении шага растет и доля случаев, когда эффективное сочетание факторов не будет найдено. При 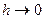 эффективный поиск сводится к методу Монте-Карло. В этом методе отсутствует статистическая проверка значимости коэффициентов регрессии.
эффективный поиск сводится к методу Монте-Карло. В этом методе отсутствует статистическая проверка значимости коэффициентов регрессии.
Из предложенных подходов построения регрессионной модели выделяют первый, основанный на оценке значимости коэффициентов регрессии по критерию Стьюдента.
2.5. Измерение интенсивности множественной связи. Выше мы показали, что при проведении социально-экономических исследований часто изучаются связи между более чем двумя явлениями. Для оценки интенсивности такой связи используется коэффициент множественной корреляции (совокупный коэффициент корреляции), который характеризует тесноту связи одной из переменных с совокупностью других.
В качестве оценки интенсивности связи между результативным признаком Y и совокупностью факторных признаков 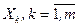 , используется величина
, используется величина
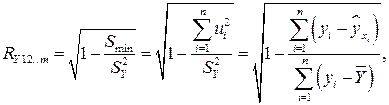 (2.10)
(2.10)
где 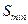 - наименьшее значение суммы
- наименьшее значение суммы
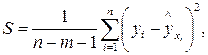
которая характеризует соответствие регрессии опытным данным, т.e. рассеяние значений 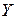 , которое возникает из-за случайностей и изменчивости прочих неучтенных факторов. Из формулы (2.10) видно, что чем меньше значение
, которое возникает из-за случайностей и изменчивости прочих неучтенных факторов. Из формулы (2.10) видно, что чем меньше значение 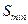 , тем меньше опытные данные
, тем меньше опытные данные 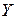 отклоняются от значений регрессии
отклоняются от значений регрессии 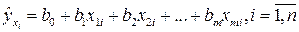 .
.
Величина R, вычисляемая по формуле (2.10), называется коэффициентом множественной корреляции (совокупным коэффициентом корреляции).
Средняя квадратичная ошибка коэффициента множественной корреляции определяется по формуле
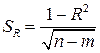 ,
,
где n-число наблюдений; m-число параметров уравнения регрессии.
Используя значения параметров 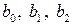 уравнения (2.4), найденных при решении системы нормальных уравнений (2.5), формулу (2.10) преобразуем к виду
уравнения (2.4), найденных при решении системы нормальных уравнений (2.5), формулу (2.10) преобразуем к виду
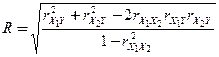 (2.11)
(2.11)
(см. [2, § 9.7]), где  - коэффициенты парной корреляции между переменными
- коэффициенты парной корреляции между переменными 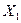 и
и 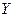 ,
,  и Y,
и Y, 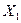 и
и  .
.
Коэффициент множественной корреляции удовлетворяет следующим свойствам:
1) его значения удовлетворяют неравенству 0 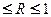 ;
;
2) если R = 0, то результативный признак Y и факторныепризнаки не могут быть связаны линейной регрессионной зависимостью, хотя нелинейная зависимость может существовать;
3) если R = 1, то результативный признак Y и факторные 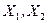 признаки связаны линейной функциональной зависимостью.
признаки связаны линейной функциональной зависимостью.
Из формулы (2.11) следует также, что если R стремится к единице, то теснота линейной корреляционной зависимости между переменными 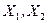 и Y увеличивается, так как
и Y увеличивается, так как 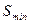 стремится при этом к нулю, т.е. опытные данные меньше отклоняются от значений регрессии.
стремится при этом к нулю, т.е. опытные данные меньше отклоняются от значений регрессии.
Об уровне тесноты множественной корреляционной связи между факторными признаками и результативным судят по значению множественного коэффициента корреляции R. Различают слабую (0,1 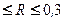 ), умеренную
), умеренную 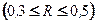 , заметную
, заметную 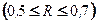 , тесную
, тесную 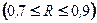 и весьма тесную
и весьма тесную 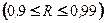 корреляционную связь.
корреляционную связь.
Отметим также, что с помощью коэффициента множественной корреляции нельзя сделать вывод о том, положительна или отрицательна корреляция между переменными. Только если все парные коэффициенты корреляции имеют один знак, можно установить характер связи между Y и
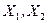 .
.
Из формулы (2.11) следует, что если коэффициент парной корреляции 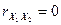 , т.е. если
, т.е. если 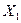 и
и  некоррелированы, то
некоррелированы, то 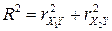 .
.
Это значит, что квадрат интенсивности связи между Yи 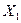 ,
,  равен сумме квадратов интенсивности связи между Y и
равен сумме квадратов интенсивности связи между Y и 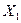 , Y и
, Y и  .
.
Коэффициент множественной корреляции можно вычислить через коэффициенты парной корреляции по формуле:
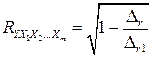 ,
,
где 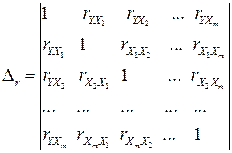 - определитель матрицы парных коэффициентов корреляции,
- определитель матрицы парных коэффициентов корреляции,
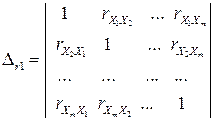 - определитель матрицы межфакторной корреляции.
- определитель матрицы межфакторной корреляции.
Связь коэффициента множественной корреляции с нормированными коэффициентами регрессии 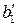 и
и 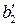 выражается формулой
выражается формулой
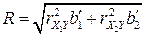 ,
,
которая обобщается на случай любого конечного числа факторных признаков, т.е.
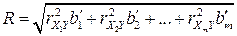 .
.
Как и в случае простой линейной регрессии, для установления того, какая часть общей дисперсии может быть объяснена зависимостью переменной Y от переменных 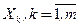 , вычисляюткоэффициент множественной детерминации
, вычисляюткоэффициент множественной детерминации
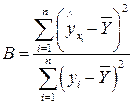 ,
,
где 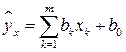 ;
; 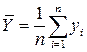 ;
; 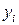 - опытные данные. Его свойства и формула аналогичны свойствам и формуле простой линейной регрессии. Если B = 1, то между Y и
- опытные данные. Его свойства и формула аналогичны свойствам и формуле простой линейной регрессии. Если B = 1, то между Y и 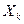 ,
,  , существует линейная функциональная зависимость; если же B = 0, то линейная зависимость отсутствует.
, существует линейная функциональная зависимость; если же B = 0, то линейная зависимость отсутствует.
При пошаговом построении уравнения регрессии важно отметить изменение множественного коэффициента детерминации. Если при введении новых факторов в уравнение регрессии множественный коэффициент детерминации увеличивается, то вводимые факторы существенны. В противном случае вводимые факторы несущественны и их можно исключить из уравнения регрессии.
Если уравнение множественной регрессии содержит только два факторных признака 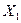 и
и  то его можно представить в виде
то его можно представить в виде
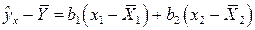 .
.
Возведем в квадрат обе части данного равенства и просуммируем все отклонения. Тогда, так как
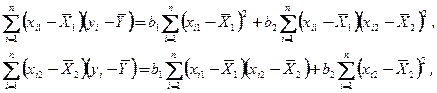
Дата добавления: 2015-08-20; просмотров: 1654;
