Парная регрессия и корреляция 3 страница
Значимость коэффициента корреляции можно определить, если воспользоваться критическими значениями коэффициента корреляции
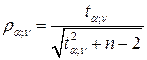 .
.
Существуют подробные таблицы критических значений коэффициента корреляции. При этом, если 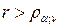 , то можно утверждать, что связь между переменными существенная; если же
, то можно утверждать, что связь между переменными существенная; если же 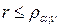 , то нет причин на основании выборки отклонить нулевую гипотезу об отсутствии связи.
, то нет причин на основании выборки отклонить нулевую гипотезу об отсутствии связи.
В случае, если при формулировке гипотезы 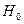 нельзя предположить, что коэффициент корреляции генеральной совокупности
нельзя предположить, что коэффициент корреляции генеральной совокупности 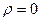 и, следовательно, нельзя положить
и, следовательно, нельзя положить 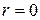 , применяют z – преобразование Фишера
, применяют z – преобразование Фишера

к статистике t и получают статистику
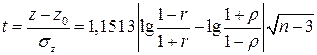 ,
,
которая имеет t-распределение с 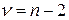 степенями свободы. Процедура проверки значимости проводится далее аналогично предыдущей.
степенями свободы. Процедура проверки значимости проводится далее аналогично предыдущей.
Иногда возникает необходимость проверки гипотезы об отличии друг от друга двух коэффициентов корреляции. При этом предполагается, что рассматриваются одни и те же признаки однородных совокупностей: данные представляют собой результаты независимых испытаний и применяются коэффициенты корреляции одного типа (коэффициенты парной или частной корреляции при исключении одинакового количества переменных). Объемы двух выборок могут быть различны. Нулевая гипотеза формируется в виде  (коэффициенты корреляции двух рассматриваемых совокупностей равны). Альтернативная гипотеза
(коэффициенты корреляции двух рассматриваемых совокупностей равны). Альтернативная гипотеза 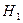 состоит в том, что
состоит в том, что 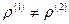 . Для проверки нулевой гипотезы используется статистика
. Для проверки нулевой гипотезы используется статистика
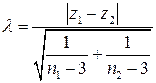 ,
,
где  – значения z - преобразования Фишера коэффициентов корреляции
– значения z - преобразования Фишера коэффициентов корреляции  и
и 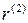 ;
; 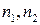 – объемы выборок.
– объемы выборок.
Если 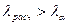 (
( 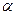 = 0,05 или
= 0,05 или 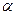 = 0,01), то гипотеза
= 0,01), то гипотеза 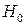 отвергается. В противном случае, т.е. при
отвергается. В противном случае, т.е. при 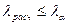 , гипотеза
, гипотеза 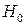 принимается. В случае принятия гипотезы
принимается. В случае принятия гипотезы 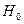 величина
величина
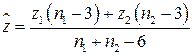
после преобразования
 tank
tank 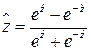
может служить оценкой коэффициента корреляции 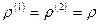 . Затем проверяется гипотеза
. Затем проверяется гипотеза 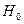 состоящая в том, что
состоящая в том, что 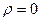 , с помощью статистики
, с помощью статистики
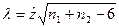
имеющей нормальное распределение.
Для проверки значимости коэффициента детерминации выдвигаются следующие гипотезы:
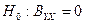 – переменная X, включенная в регрессию, не оказывает существенного влияния на зависимую переменную
– переменная X, включенная в регрессию, не оказывает существенного влияния на зависимую переменную 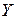 ;
;
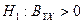 – переменная X, включенная в регрессию, оказывает существенное влияние на зависимую переменную
– переменная X, включенная в регрессию, оказывает существенное влияние на зависимую переменную 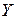 ;
;
В этом случае для проверки гипотезы следует использовать одностороннюю критическую область. Для оценки значимости парного коэффициента детерминации 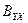 используется статистика
используется статистика
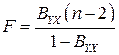 ,
,
имеющая F-распределение Фишера с 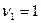 и
и 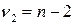 степенями свободы.
степенями свободы.
Значение статистики, вычисленное по результатам выборки, сравнивается с критическим значением  , найденным по таблице F-распределения Фишера при заданном уровне значимости
, найденным по таблице F-распределения Фишера при заданном уровне значимости 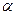 и соответствующем числе степеней свободы. Если
и соответствующем числе степеней свободы. Если  , то вычисленный коэффициент парной детерминации значимо (с вероятностью
, то вычисленный коэффициент парной детерминации значимо (с вероятностью 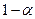 ) отличается от нуля и, следовательно, переменная
) отличается от нуля и, следовательно, переменная 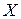 оказывает существенное влияние на переменную
оказывает существенное влияние на переменную 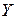 .
.
1.9. Оценка адекватности регрессионной модели.После проверкизначимости коэффициентов регрессии проверяется общее качество уравнения регрессии, т.е. проверяется, насколько хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Для подтверждения факта непротиворечивости формы зависимости опытным данным либо опровержения предложенного вида зависимости как не соответствующей этим данным разработаны различные статистические критерии.
Линейность регрессии проверяется, используя следующий прием.
Пусть  – групповое среднее, соответствующее
– групповое среднее, соответствующее 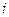 -му значению переменной X, вычисляемое по формуле
-му значению переменной X, вычисляемое по формуле
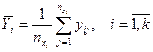 ,
,
где 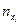 – число значений переменной Y, относящихся к
– число значений переменной Y, относящихся к 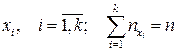 .
.
Как отмечалось, сумму
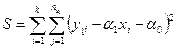
можно представить в виде четырех слагаемых: 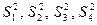 . Тогда если в генеральной совокупности существует линейная регрессия и условные распределения переменной Y хотя бы приблизительно нормальны, то отношение
. Тогда если в генеральной совокупности существует линейная регрессия и условные распределения переменной Y хотя бы приблизительно нормальны, то отношение 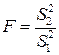 средних квадратов отклонений
средних квадратов отклонений
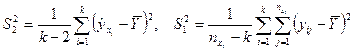 (1.7)
(1.7)
имеет F-распределение с 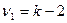 и
и  степенями свободы. Расчетное значение
степенями свободы. Расчетное значение 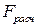 =
= 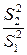 сравнивается с квантилем
сравнивается с квантилем 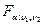 , найденным по таблице
, найденным по таблице 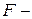 распределения при заданном уровне значимости
распределения при заданном уровне значимости 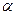 и
и 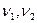 степенях свободы. Если
степенях свободы. Если 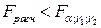 , то линейная регрессионная зависимость не противоречит опытным данным. В противном случае, т.е. если
, то линейная регрессионная зависимость не противоречит опытным данным. В противном случае, т.е. если 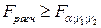 , гипотеза о линейной зависимости между переменными несостоятельна.
, гипотеза о линейной зависимости между переменными несостоятельна.
Для проверки статистической адекватности уравнения регрессии (общего качества уравнения регрессии) обычно используют три критерия:
1) проводят анализ дисперсии зависимой переменной Y;
2) определяют стандартную ошибку по формуле
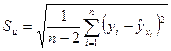 ;
;
3) вычисляют среднюю абсолютную процентную ошибку аппроксимации:
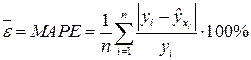 .
.
1) Анализ дисперсии зависимой переменной состоит в том, что сумма 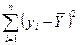 представляется в виде суммы двух слагаемых:
представляется в виде суммы двух слагаемых:
 .
.
Затем составляется отношение средних значений этих сумм:
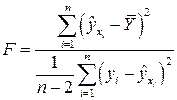 ,
,
которое используется в качестве статистики для проверки гипотезы 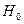 , состоящей в том, что
, состоящей в том, что 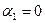 . Эта выборочная статистика характеризуется F-распределением с
. Эта выборочная статистика характеризуется F-распределением с 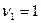 и
и 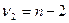 степенями свободы. По таблице F-распределения для заданного уровня значимости
степенями свободы. По таблице F-распределения для заданного уровня значимости 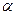 и числа степеней свободы
и числа степеней свободы  и
и 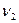 находим квантиль
находим квантиль 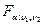 , с которым сравниваем
, с которым сравниваем 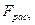 . Если
. Если  , то уравнение регрессии признается значимым, т.е. доля вариации, отнесенная за счет уравнения регрессии, больше, чем за счет случайных неучтенных факторов. Считается, что уравнение регрессии адекватно изучаемому экономическому процессу, если
, то уравнение регрессии признается значимым, т.е. доля вариации, отнесенная за счет уравнения регрессии, больше, чем за счет случайных неучтенных факторов. Считается, что уравнение регрессии адекватно изучаемому экономическому процессу, если 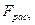 в 4 раза больше квантиля
в 4 раза больше квантиля 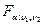 F-распределения.
F-распределения.
Построенное уравнение регрессии можно использовать для прогнозирования значений зависимой переменной по значениям переменной X. Для этого конкретное значение 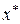 подставляем в эмпирическое уравнение регрессии и находим значение
подставляем в эмпирическое уравнение регрессии и находим значение 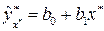 . Значение
. Значение 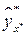 является оценкой условного математического ожидания
является оценкой условного математического ожидания 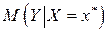 переменной
переменной 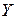 при
при 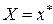 . При этом возникает вопрос , на сколько отклоняется прогнозное значение
. При этом возникает вопрос , на сколько отклоняется прогнозное значение 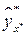 от соответствующего условного математического ожидания
от соответствующего условного математического ожидания 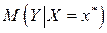 . Ответ на этот вопрос дается на основе интервальной оценки, построенной с заданной надежностью
. Ответ на этот вопрос дается на основе интервальной оценки, построенной с заданной надежностью 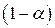 . Соответствующий доверительный интервал для условного математического ожидания имеет вид:
. Соответствующий доверительный интервал для условного математического ожидания имеет вид: 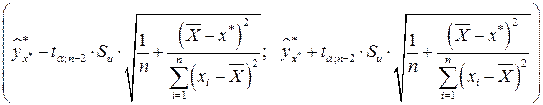 ,
,
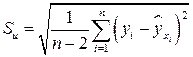 .
.
2) Ясно, что действительные значения Y рассеяны вокруг линии регрессии. Первым и наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогностических оценок, является рассеяние наблюдений вокруг линии регрессии. В качестве меры рассеяния принимается величина
 .
.
Она является выборочной оценкой дисперсии случайных чисел 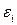 , содержащихся в теоретической модели
, содержащихся в теоретической модели  . Ясно, что чем меньше
. Ясно, что чем меньше  , тем модель будет более адекватной изучаемому экономическому процессу.
, тем модель будет более адекватной изучаемому экономическому процессу.
3) Средняя абсолютная процентная ошибка характеризует в процентах среднее отклонений значений зависимой переменной Y от уравнения регрессии. Если 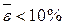 , то модель имеет высокую точность; если 10%<
, то модель имеет высокую точность; если 10%<  <20%, то модель имеет хорошую точность (допустимую); при
<20%, то модель имеет хорошую точность (допустимую); при  , точность модели удовлетворительная. Если
, точность модели удовлетворительная. Если 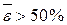 , то точность модели неудовлетворительная и ее использование недопустимо. Модель считается адекватной, если не превосходит 20%.
, то точность модели неудовлетворительная и ее использование недопустимо. Модель считается адекватной, если не превосходит 20%.
Чтобы иметь полную уверенность в адекватности модели, нужно выполнить проверку случайности остатков  .
.
1.10. Пример построения однофакторной регрессионной модели. Исследуем зависимость выпуска валовой продукции на одного среднегодового работника сельского хозяйства (Y , день. ед.) от фондовооруженности одного работника, занятого в сельскохозяйственном производстве (X, тыс. ден. ед. на человека), по данным 30 колхозов Республики Беларусь (табл. 1.4). Фондовооруженность выбрана в качестве факторного признака исходя из экономических соображений. Спрогнозируем выпуск валовой продукции при фондовооруженности 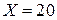 тыс. ден.ед., построим доверительный интервал для данного прогноза.
тыс. ден.ед., построим доверительный интервал для данного прогноза.
Из расположения точек 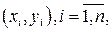 на корреляционном поле предположим линейную связь между переменными. Эмпирическую прямую регрессии
на корреляционном поле предположим линейную связь между переменными. Эмпирическую прямую регрессии 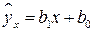 построим, используя ПЭВМ (программа АРМС).
построим, используя ПЭВМ (программа АРМС).
Т а б л и ц а 1.4
| X | Y | X | Y | X | Y | ||
| 14,482 14,397 12,280 10,397 14,888 12,012 12,819 12,626 13,444 15,043 | 17,627 14,470 13,096 14,449 16,526 14,389 16,479 14,678 15,995 11,472 | 13,837 14,153 15,957 16,804 13,752 13,795 15,420 18,342 13,642 19,856 |
Оцениваемую линейную корреляционную связь можно представить в виде эмпирического уравнения регрессии:
 .
.
Проверим значимость коэффициента регрессии  . Для этого выдвинем гипотезу
. Для этого выдвинем гипотезу 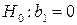 состоящую в том, что переменная X не оказывает существенного влияния на зависимую переменную Y, против альтернативной гипотезы
состоящую в том, что переменная X не оказывает существенного влияния на зависимую переменную Y, против альтернативной гипотезы 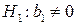 . Статистика
. Статистика
 .
.
По таблице t-распределения для уровня значимости 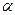 = 0,05 и
= 0,05 и 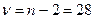 степеней свободы находим критическое значение статистики:
степеней свободы находим критическое значение статистики: 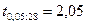 (при двусторонней критической области). Так как
(при двусторонней критической области). Так как 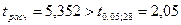 , то фондовооруженность, переменная X, оказывает существенное влияние на валовую продукцию, переменная Y.
, то фондовооруженность, переменная X, оказывает существенное влияние на валовую продукцию, переменная Y.
В рассматриваемом примере коэффициент регрессии показывает, что валовая продукция в среднем возрастает на 541,4 ден. ед., если фондовооруженность увеличивается на 1 тыс. ден. ед. . Коэффициент регрессии отражает влияние изменения уровня фондовооруженности на объем выпуска валовой продукции.
Оценим интенсивность связи между фондовооруженностью и объемом выпуска валовой продукции, используя коэффициент корреляции. Так как коэффициент линейной корреляции 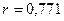 , то между изучаемыми факторами существует тесная корреляционная связь.
, то между изучаемыми факторами существует тесная корреляционная связь.
Проверим значимость коэффициента корреляции, выдвинув нулевую гипотезу  : различие между r и
: различие между r и 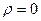 незначимо, и альтернативную гипотезу
незначимо, и альтернативную гипотезу 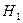 : различие между r и
: различие между r и 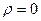 значимо. Вычисленную по результатам выборки статистику
значимо. Вычисленную по результатам выборки статистику
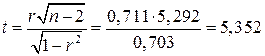
сравним с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости 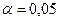 и
и  степенях свободы:
степенях свободы: 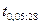 (воспользовались двусторонней критической областью). Так как
(воспользовались двусторонней критической областью). Так как 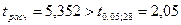 , то гипотеза
, то гипотеза  отвергается на уровне значимости 0,05. С вероятностью
отвергается на уровне значимости 0,05. С вероятностью 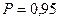 можно утверждать, что между фондовооруженностью и объемом выпуска валовой продукции существует тесная корреляционная зависимость.
можно утверждать, что между фондовооруженностью и объемом выпуска валовой продукции существует тесная корреляционная зависимость.
Исследуем адекватность построенной однофакторной модели изучаемому экономическому процессу. Вычисленное по результатам выборки F-отношение равно  . Сравниваем его с квантилем табличного F-распределения, определенного при уровне значимости
. Сравниваем его с квантилем табличного F-распределения, определенного при уровне значимости 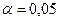 и
и  и
и 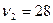 степенях свободы:
степенях свободы: 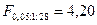 . Так как
. Так как 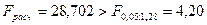 , то уравнение регрессии с вероятностью
, то уравнение регрессии с вероятностью 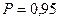 признается значимым.
признается значимым.
Используем остатки в качестве характеристики степени согласованности расчетных значений регрессии и наблюдаемых значений переменной Y.
Подставив в полученное уравнение регрессии значения  из табл. 2.18, вычислим значения регрессии
из табл. 2.18, вычислим значения регрессии  и остатки
и остатки  .
.
Стандартная ошибка остатков рассматривается как стандартная ошибка оценки регрессии в связи с интерпретацией возмущающей переменной U как результата ошибки спецификации функции регрессии. Находим несмещенную оценку дисперсии возмущающих воздействий  :
:
 ,
,
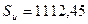 .
.
Из значений остатков следует, что необходимо прежде всего проанализировать деятельность колхозов с номерами 26, 4, 13, 23, 29, 30, 5, 16, 17 и 7, показатели которых отличаются большими отклонениями в ту и другую стороны от значений, предсказанных по уравнению регрессии. В колхозах, для которых обнаружены отрицательные отклонения фактических значений от расчетных, следовало бы уделить особое внимание экономической и организационной работе.
Среднеабсолютная процентная ошибка, вычисленная для данных рассматриваемого примера,
 ,
,
что свидетельствует о высокой точности построенного уравнения регрессии.
Для определения того, какая часть полного рассеяния значений Y обусловлена изменчивостью переменной X, вычислим коэффициент детерминации. Так как 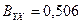 , делаем вывод, что только 50,6% общей дисперсии объема выпуска валовой продукции в рассматриваемых колхозах обусловлено вариацией фондовооруженности. Это значит, что в регрессионную модель нужно вводить дополнительные факторы, оказывающие влияние на объем выпуска валовой продукции. Коэффициент неопределенности
, делаем вывод, что только 50,6% общей дисперсии объема выпуска валовой продукции в рассматриваемых колхозах обусловлено вариацией фондовооруженности. Это значит, что в регрессионную модель нужно вводить дополнительные факторы, оказывающие влияние на объем выпуска валовой продукции. Коэффициент неопределенности 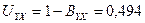 , или 49,4%. Следовательно, 49,4% общей дисперсии нельзя объяснить зависимостью объема выпуска валовой продукции от фондовооруженности.
, или 49,4%. Следовательно, 49,4% общей дисперсии нельзя объяснить зависимостью объема выпуска валовой продукции от фондовооруженности.
Таким образом, из анализа всех показателей адекватности модели следует, что уравнение регрессии статистически значимо, но в построенную модель следует ввести еще ряд факторов, влияющих на объем выпуска валовой продукции.
Подставив в построенное эмпирическое уравнение регрессии значение фондовооруженности 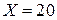 найдем прогнозное значение объема выпуска валовой продукции
найдем прогнозное значение объема выпуска валовой продукции 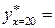 13 390 ден.ед. Соответствующий доверительный интервал буде иметь вид:
13 390 ден.ед. Соответствующий доверительный интервал буде иметь вид:
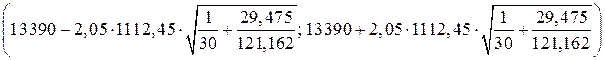 =
=
= (12 191,188; 14 588,812).
Следовательно, средний объем выпуска валовой продукции при фондовооруженности 20 ден. ед. будет находиться в интервале (12 191,188; 14 588,812).
2. Многофакторные регрессионные модели
2.1. Построение многофакторной линейной регрессионной модели. Связи между массовыми экономическими явлениями характеризуются тем, что в действительности некоторое явление детерминируется множеством одновременно и совокупно действующих причин. Поэтому в общем случае зависимая переменная может быть функцией нескольких переменных 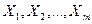 и вместо парной регрессии рассматривается множественная регрессия:
и вместо парной регрессии рассматривается множественная регрессия:  .
.
В каждом 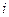 -м наблюдении получаем совокупность значений независимых переменных
-м наблюдении получаем совокупность значений независимых переменных 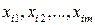 и соответствующее значение зависимой переменной
и соответствующее значение зависимой переменной 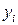 .
.
Предположим, что между независимыми переменными 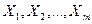 и зависимой переменной Y существует линейное соотношение. Тогда уравнение
и зависимой переменной Y существует линейное соотношение. Тогда уравнение

выражающее линейное соотношение между переменными, называется теоретическим уравнением множественной регрессии, а соответствующее эмпирическое уравнение регрессии будет иметь вид:
 , (2.1)
, (2.1)
Ясно, что указанным уравнением невозможно охватить весь комплекс причин и учесть случайность, присущую в тои или иной степени причинному действию и определенному им следствию. Ограничиваясь наиболее важными факторами, влияющими на развитие исследуемого явления, в выражение функции регрессии вводят аддитивную составляющую – возмущающую переменную U, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Возмущение и является случайной переменной, математическое ожидание 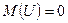 , дисперсия возмущений U постоянна. Поэтому эмпирическое значение величины Y можно представить следующим образом:
, дисперсия возмущений U постоянна. Поэтому эмпирическое значение величины Y можно представить следующим образом:
 . (2.2)
. (2.2)
В выражении (2.1) 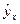 – это среднее значение переменной Y в точке i при фиксированных значениях
– это среднее значение переменной Y в точке i при фиксированных значениях 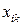 независимых переменных
независимых переменных 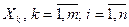 , в предположении, что только эти m переменных являются причиной изменения переменной Y. Значения
, в предположении, что только эти m переменных являются причиной изменения переменной Y. Значения  – это оценки коэффициентов регрессии
– это оценки коэффициентов регрессии  . Так, например,
. Так, например, 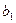 указывает среднюю величину изменения Y при изменении
указывает среднюю величину изменения Y при изменении 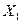 на одну единицу при условии, что другие переменные остаются без изменения;
на одну единицу при условии, что другие переменные остаются без изменения; 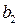 указывает среднюю величину изменения Y при изменении
указывает среднюю величину изменения Y при изменении  на одну единицу при условии, что другие переменные остались без изменения, и т.д. Свободный член регрессии
на одну единицу при условии, что другие переменные остались без изменения, и т.д. Свободный член регрессии 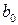 определяет точку пересечения гиперповерхности регрессии с осью ординат. Итак, регрессия (2.1) охватывает совокупное одновременное влияние независимых переменных, а коэффициенты регрессии
определяет точку пересечения гиперповерхности регрессии с осью ординат. Итак, регрессия (2.1) охватывает совокупное одновременное влияние независимых переменных, а коэффициенты регрессии  , указывают соответствующие усредненные частные влияния переменных
, указывают соответствующие усредненные частные влияния переменных 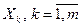 , в предположении, что остальные независимые переменные сохраняются на постоянном уровне.
, в предположении, что остальные независимые переменные сохраняются на постоянном уровне.
Обозначив через 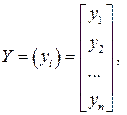 , матрицу-столбец зависимой переменной; через
, матрицу-столбец зависимой переменной; через 
 матрицу независимых переменных, размер которой определяется числом наблюдений n и числом переменных m; через
матрицу независимых переменных, размер которой определяется числом наблюдений n и числом переменных m; через 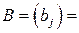
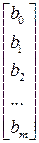 матрицу-столбец коэффициентов регрессии; через
матрицу-столбец коэффициентов регрессии; через 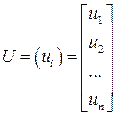 матрицу-столбец возмущений, перепишем линейную модель (2.2) в виде
матрицу-столбец возмущений, перепишем линейную модель (2.2) в виде
Дата добавления: 2015-08-20; просмотров: 1536;
