Парная регрессия и корреляция 2 страница
Т а б л и ц а 1.1
| Корреляционная зависимость | Значение коэффициента корреляции |
| Слабая Умеренная Заметная Тесная Весьма тесная | 0,1 < r < 0,3, -0,3 < r < -0,1 0,3 < r < 0,5, -0,5 < r < -0,3 0,5 < r < 0,7, -0,7 < r < -0,5 0,7 < r < 0,9, -0,9 < r < -0,7 0,9 < r < 0,99, -0,99 < r < -0,9 |
Отметим, что коэффициент корреляции не отражает направление зависимости, т.е. он является функцией, симметричной относительно X и Y.
Средняя квадратичная ошибка коэффициента корреляции определяется по формуле
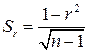 .
.
Наряду с коэффициентом корреляции и корреляционным отношением в эконометрике применяется коэффициент детерминации, отражающий, в какой мере функция регрессии определяется факторными признаками, содержащимися в ней.
Для определения коэффициента детерминации дисперсию, характеризующую рассеяние наблюдаемых значений переменной 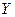 около ее среднего, разложим на две составляющие:
около ее среднего, разложим на две составляющие:
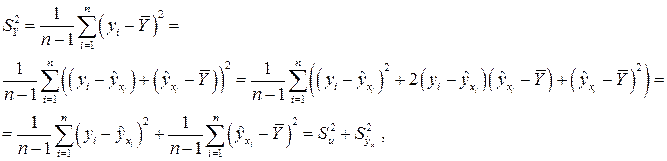
где 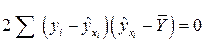 , так как прямая регрессии проходит через среднюю точку
, так как прямая регрессии проходит через среднюю точку 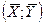 корреляционного поля.
корреляционного поля.
Дисперсия 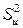 представляет собой ту часть общей дисперсии
представляет собой ту часть общей дисперсии 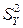 , которая обусловлена случайностью и изменчивостью прочих неучтенных факторов и не объясняется функцией регрессии. Из равенства
, которая обусловлена случайностью и изменчивостью прочих неучтенных факторов и не объясняется функцией регрессии. Из равенства
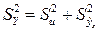
видно, что чем меньше 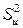 , тем меньше эмпирические значения
, тем меньше эмпирические значения 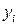 отклоняются от значений регрессии
отклоняются от значений регрессии 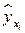 . Вторая составляющая общей дисперсии
. Вторая составляющая общей дисперсии 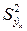 является дисперсией значений регрессии
является дисперсией значений регрессии 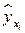 . Рассеяние значений регрессии определяется значением коэффициента регрессии, следовательно, дисперсия
. Рассеяние значений регрессии определяется значением коэффициента регрессии, следовательно, дисперсия 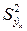 обусловлена влиянием факторного признака. Поэтому чем больше
обусловлена влиянием факторного признака. Поэтому чем больше 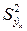 по сравнению с
по сравнению с 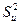 , тем больше общая дисперсия формируется за счет влияния факторного признака и, следовательно, связь между двумя переменными
, тем больше общая дисперсия формируется за счет влияния факторного признака и, следовательно, связь между двумя переменными 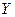 и X более интенсивная. Тогда в качестве показателя интенсивности связи (или оценки доли влияния переменной X на
и X более интенсивная. Тогда в качестве показателя интенсивности связи (или оценки доли влияния переменной X на 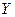 ) используется отношение
) используется отношение
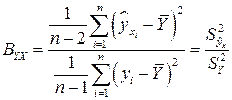 ,
,
которое указывает, какая часть общего рассеяния значений Y обусловлена изменчивостью переменной X, и называется коэффициентом детерминации. Чем большую долю в общей дисперсии составляет 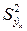 , тем лучше выбранная функция регрессии соответствует эмпирическим данным.
, тем лучше выбранная функция регрессии соответствует эмпирическим данным.
Коэффициент детерминации 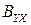 изменяется в пределах от 0 до 1
изменяется в пределах от 0 до 1 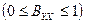 . Если
. Если 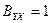 , то все эмпирические значения
, то все эмпирические значения 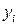 лежат на регрессионной прямой, т.е.
лежат на регрессионной прямой, т.е. 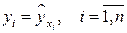 , и
, и 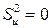 . Следовательно, переменные X и Y связаны линейной функциональной зависимостью. Если
. Следовательно, переменные X и Y связаны линейной функциональной зависимостью. Если 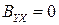 , то
, то 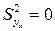 , а «остаточная» дисперсия
, а «остаточная» дисперсия 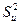 равна общей дисперсии
равна общей дисперсии 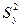 , т.е.
, т.е. 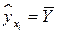 . В этом случае линия регрессии параллельна оси абсцисс и, следовательно, ни о какой статистической линейной зависимости не может быть речи.
. В этом случае линия регрессии параллельна оси абсцисс и, следовательно, ни о какой статистической линейной зависимости не может быть речи.
Таким образом, чем больше коэффициент детерминации 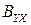 приближается к единице, тем лучше определена регрессия.
приближается к единице, тем лучше определена регрессия.
Коэффициент детерминации 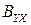 – величина безразмерная. Он не зависит от единиц измерения признаков X и Y и не изменяется при преобразовании переменных.
– величина безразмерная. Он не зависит от единиц измерения признаков X и Y и не изменяется при преобразовании переменных.
Подставляя выражения

в формулу 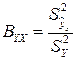 , получаем:
, получаем:

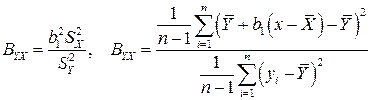 ,
,
откуда, так как
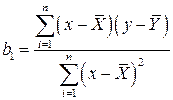 ,
,
выводим формулу коэффициента детерминации, удобную для вычисления:
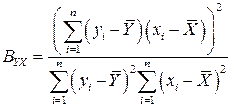 .
.
Укажем соотношения между коэффициентами корреляции, регрессии и детерминации при однофакторной линейной регрессии:
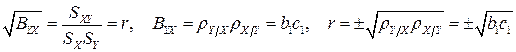 ,
,
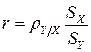 или
или 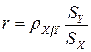
(перед корнем ставится знак коэффициента регрессии).
1.7. Нелинейная регрессия и корреляция. Подбор функции регрессии должен производиться с применением теории конкретной науки, на базе которой формулируется задача измерения связи между явлениями. При этом следует использовать методы выявления наличия связи. Односторонняя стохастическая зависимость может быть выражена и при помощи нелинейных функций. Различают два класса нелинейных регрессий. К первому классу относятся функции, нелинейные относительно факторного признака, но линейные относительно параметров, входящих в данные функции. Для оценок параметров таких функций применяется метод наименьших квадратов, следовательно, остаются в силе все исходные предпосылки линейного регрессионного анализа. Второй класс регрессий характеризуется нелинейностью факторного признака, входящего в уравнение регрессии.
Т а б л и ц а 1.2
| Функция | Нормальные уравнения |
1. 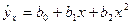
| 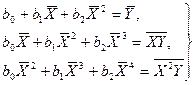
|
2. 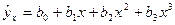
| 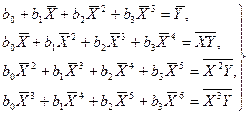
|
3. 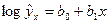
| 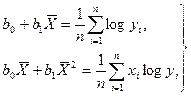
|
4. 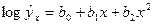
| 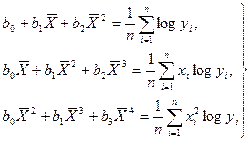
|
5. 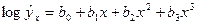
| Такие же, как и для функции 2 при замене 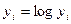 
|
6. 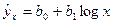
| 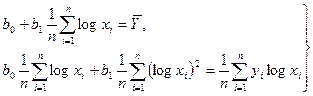
|
7. 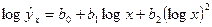
| Такие же, как для функции 1
при замене 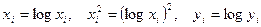
|
8. 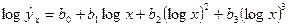
| Такие же, как для функции 2
при замене 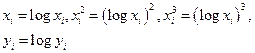
|
9. 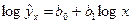
| 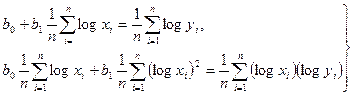
|
10. 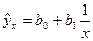
| 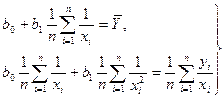
|
11. 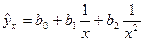
| Такие же, как для функции 1
при замене 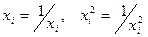
|
Функции, наиболее часто встречающиеся в однофакторных регрессионных моделях, представлены в табл. 1.2 (квазилинейные функции) и 1.3 (нелинейные функции второго класса), где даны также нормальные уравнения для определения входящих в них параметров и преобразованные функции (для нелинейных функций второго класса).
Т а б л и ц а 1.3
| Название функции | Аналитическое выражение | Преобразование |
| Степенная | 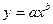
| 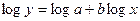
|
| Показательная | 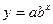
| 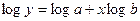
|
| Показательно-степенная | 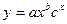
| 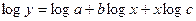
|
| Экологическая | 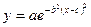
| 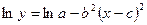
|
| Логистическая | 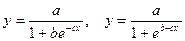
| 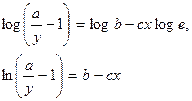
|
| Частный случаи логической функции | 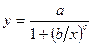
| 
|
| Гомперца | 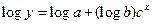
| 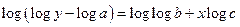
|
| Иррациональная | 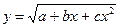
| 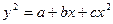
|
| Гиперболическая | 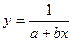
| 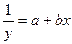
|
| Обратная квадратному трехчлену | 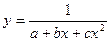
| 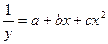
|
| Дробно-рациональная | 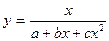
| 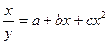
|
| Джонсона | 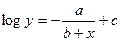
| 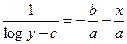
|
| Модифицированная экспоненциальная | 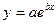
| 
|
| Торнквиста: 1-го типа | 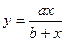
| 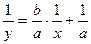
|
| 2-го типа | 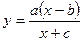
| 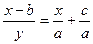
|
| 3-го типа | 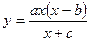
| 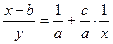
|
В табл. 1.2 и 1.3 указаны классы регрессий, характеризующихся нелинейностью относительно переменной X или относительно оцениваемых параметров. Квазилинейные функции (см. табл. 1.2) линейны относительно искомых параметров, т.е. их можно представить в виде
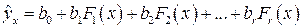 , (1.3)
, (1.3)
где 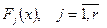 , – функции переменной X. Они не содержат параметров. Например,
, – функции переменной X. Они не содержат параметров. Например, 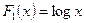 или
или 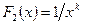 и т.д. Поэтому к функции (1.3) можно применить метод наименьших квадратов. Получим систему нормальных уравнений:
и т.д. Поэтому к функции (1.3) можно применить метод наименьших квадратов. Получим систему нормальных уравнений:
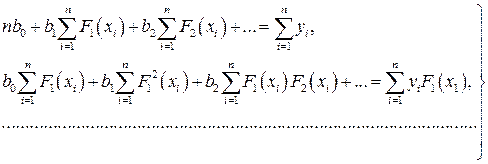
Правило составления нормальных уравнений системы состоит в следующем: первое уравнение системы получается суммированием функций 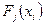 по
по 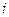 из уравнения (1.3), остальные уравнения – последовательным умножением функции регрессии (1.3) соответственно на
из уравнения (1.3), остальные уравнения – последовательным умножением функции регрессии (1.3) соответственно на 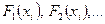 и последующим суммированием полученных результатов по
и последующим суммированием полученных результатов по 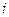 .
.
Для получения оценок параметров функций из табл. 1.3 их предварительно подвергают преобразованиям, главное назначение которых – линеаризация рассматриваемых зависимостей по оцениваемым параметрам. Параметры регрессии исходных функций находят путем обратных преобразований. Например, путем логарифмического преобразования можно перейти от зависимости показательного типа 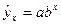 к линейной
к линейной 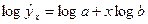 .
.
Применяя метод наименьших квадратов к функции 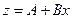 , где
, где 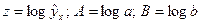 , получаем значения
, получаем значения 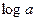 и
и 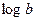 . Потенцируя полученные значения, находим оценки параметров исходной функции.
. Потенцируя полученные значения, находим оценки параметров исходной функции.
Вычислив дисперсию результативного признака 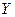 и воспользовавшись отклонениями величины
и воспользовавшись отклонениями величины 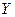 от средней величины
от средней величины 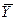 , получим показатель общей дисперсии
, получим показатель общей дисперсии 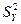 , характеризующей вариацию признака Y. Вычислив дисперсию
, характеризующей вариацию признака Y. Вычислив дисперсию 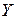 для каждого отдельного значения
для каждого отдельного значения 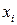 признака
признака 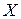 и воспользовавшись отклонениями данных значений
и воспользовавшись отклонениями данных значений 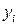 от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию
от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию 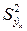 . Она меньше дисперсии
. Она меньше дисперсии 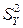 . В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий и получим корреляционное отношение, которое применяется для оценки интенсивности нелинейной связи:
. В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий и получим корреляционное отношение, которое применяется для оценки интенсивности нелинейной связи:
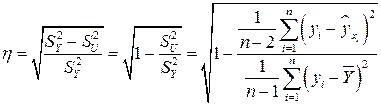 .
.
Корреляционное отношение удовлетворяет свойствам:
· Величина корреляционного отношения не зависит от выбора единиц измерения случайных величин 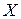 и
и 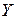 ;
;
· Корреляционное отношение не превосходит единицы, т.е. 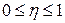 ;
;
· Корреляционное отношение 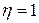 тогда и только тогда, когда между случайными величинами
тогда и только тогда, когда между случайными величинами 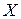 и
и 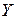 существует функциональная зависимость;
существует функциональная зависимость;
· Если между случайными величинами 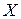 и
и 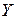 отсутствует хотя бы одна из корреляционных связей, то корреляционное отношение равно нулю;
отсутствует хотя бы одна из корреляционных связей, то корреляционное отношение равно нулю;
· Условие 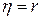 является необходимым и достаточным условием линейной регрессионной связи;
является необходимым и достаточным условием линейной регрессионной связи;
· Корреляционное отношение не меньше коэффициента корреляции 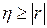 .
.
Из свойств корреляционного отношения следует, что чем больше значение корреляционного отношения приближается к единице (т. е. чем ближе нормированная разность 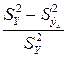 к единице), тем сильнее наблюдаемая связь, а если
к единице), тем сильнее наблюдаемая связь, а если  , то связь ослабевает. При функциональной зависимости все значения Y лежали бы на линии регрессии.
, то связь ослабевает. При функциональной зависимости все значения Y лежали бы на линии регрессии.
Для оценки интенсивности нелинейной связи используется также индекс корреляции 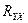 , который вычисляется по формуле:
, который вычисляется по формуле:
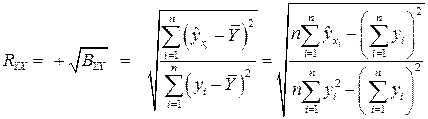 .
.
Индекс корреляции принимает значения в интервале 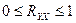 . Если
. Если 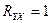 , т.е.
, т.е. 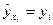 для всех
для всех 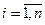 , то мы располагаем функциональной зависимостью. Если же
, то мы располагаем функциональной зависимостью. Если же 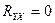 , т.е.
, т.е. 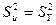 для всех
для всех 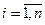 ,
, 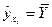 , то связь в этом случае отсутствует. Чем больше значение индекса корреляции приближается к единице, тем сильнее наблюдаемая связь.
, то связь в этом случае отсутствует. Чем больше значение индекса корреляции приближается к единице, тем сильнее наблюдаемая связь.
Средняя квадратичная ошибка корреляционного отношения
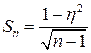 .
.
Различные уравнения регрессии, служащие для оценки уровня величин исследуемых зависимых переменных, представляют большей практический интерес, например в планировании. Оценки, полученные в уравнении регрессии, достаточно точно воспроизводят линию реальной эволюции явлений, если не слишком отдаляться от эмпирических данных. Экстраполяция допускается только тогда, когда доказана полная аналогия условий, места, времени и однородности явлений, к которым относятся оценки.
1.8. Проверка существенности оценок параметров регрессии, коэффициентов корреляции и детерминации. Мы отмечали, что оценки параметров регрессии являются случайными величинами с определенными распределениями вероятностей. При выполнении предположений 1 – 6, указанных выше, оценки параметров регрессии 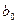 и
и 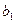 распределены нормально с математическим ожиданием
распределены нормально с математическим ожиданием 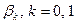 (
( 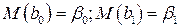 ), и дисперсией
), и дисперсией 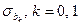 . Отсюда следует, что величина
. Отсюда следует, что величина 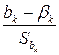 имеет стандартное нормальное распределение. Значения распределений оценок параметров регрессии позволяют производить оценку значимости соответствующих статистических характеристик. При практических исследованиях проверка значимости основывается на выборочных наблюдениях. Как всякая статистическая характеристика, параметры уравнения регрессии являются величинами случайными, т.е. их значения случайно рассеиваются вокруг одноименных параметров генеральной совокупности (истинных значений параметров теоретической регрессии). Если значения оценок параметров эмпирической регрессии попадают в зону рассеяния, обусловленную случайным характером самих показателей, это не является доказательством отсутствия регрессионной связи. Можно только утверждать, что исходные данные не отрицают отсутствия связи между переменными. Но если значения оценок параметров регрессии будут лежать вне этой зоны рассеяния, то можно считать, что между переменными существует статистически значимая связь. Используемый для решения этой задачи критерий значимости основан на распределении различных статистик.
имеет стандартное нормальное распределение. Значения распределений оценок параметров регрессии позволяют производить оценку значимости соответствующих статистических характеристик. При практических исследованиях проверка значимости основывается на выборочных наблюдениях. Как всякая статистическая характеристика, параметры уравнения регрессии являются величинами случайными, т.е. их значения случайно рассеиваются вокруг одноименных параметров генеральной совокупности (истинных значений параметров теоретической регрессии). Если значения оценок параметров эмпирической регрессии попадают в зону рассеяния, обусловленную случайным характером самих показателей, это не является доказательством отсутствия регрессионной связи. Можно только утверждать, что исходные данные не отрицают отсутствия связи между переменными. Но если значения оценок параметров регрессии будут лежать вне этой зоны рассеяния, то можно считать, что между переменными существует статистически значимая связь. Используемый для решения этой задачи критерий значимости основан на распределении различных статистик.
Практически проверка значимости начинается с формулировки нулевой гипотезы 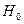 состоящей в том, что между параметром выборки и параметром генеральной совокупности имеется существенное различие. Альтернативная гипотеза
состоящей в том, что между параметром выборки и параметром генеральной совокупности имеется существенное различие. Альтернативная гипотеза 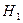 утверждает, что между этими параметрами не имеется существенного различия. Затем устанавливается уровень значимости
утверждает, что между этими параметрами не имеется существенного различия. Затем устанавливается уровень значимости  , выражающий вероятность того, что нулевая гипотеза
, выражающий вероятность того, что нулевая гипотеза 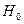 отвергается в то время, когда она в действительности верна. При проверке существенности параметров корреляционно-регрессионной связи выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи. Если требуется оценить абсолютную величину расхождения между параметрами выборки и генеральной совокупности, то используется двусторонняя критическая область. Если же требуется установить, что один из параметров строго больше или меньше другого, то используется односторонняя критическая область. Уровень значимости, при использовании односторонней критической области меньше, чем при использовании двусторонней. В случае симметричного распределения выборочной характеристики уровень значимости двусторонней критической области равен
отвергается в то время, когда она в действительности верна. При проверке существенности параметров корреляционно-регрессионной связи выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи. Если требуется оценить абсолютную величину расхождения между параметрами выборки и генеральной совокупности, то используется двусторонняя критическая область. Если же требуется установить, что один из параметров строго больше или меньше другого, то используется односторонняя критическая область. Уровень значимости, при использовании односторонней критической области меньше, чем при использовании двусторонней. В случае симметричного распределения выборочной характеристики уровень значимости двусторонней критической области равен 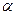 , а односторонней
, а односторонней 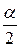 . Затем задается статистическая характеристика (статистика) для проверки гипотезы
. Затем задается статистическая характеристика (статистика) для проверки гипотезы 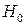 . Более подробное теоретическое обоснование проверки статистических гипотез можно найти в учебном пособии (2, § 8.1).
. Более подробное теоретическое обоснование проверки статистических гипотез можно найти в учебном пособии (2, § 8.1).
Рассмотрим проверку значимости параметров корреляционно-регрессионного анализа. Для оценки значимости каждого параметра регрессии выдвинем следующие гипотезы:
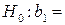 0 – переменная X не оказывает существенного влияния на зависимую переменную Y;
0 – переменная X не оказывает существенного влияния на зависимую переменную Y;
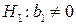 – переменная X оказывает существенное влияние на зависимую переменную Y.
– переменная X оказывает существенное влияние на зависимую переменную Y.
При такой альтернативной гипотезе 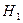 используется двусторонняя критическая область. Если же альтернативная гипотеза
используется двусторонняя критическая область. Если же альтернативная гипотеза 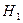 формулируется в виде
формулируется в виде 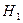 :
: 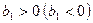 , т.е. имеется значимая положительная (отрицательная) зависимость переменной Y от переменной X, то используется односторонняя критическая область. Ясно, что при такой формулировке альтернативной гипотезы на основании экономических соображений должен быть априори известен знак параметра регрессии.
, т.е. имеется значимая положительная (отрицательная) зависимость переменной Y от переменной X, то используется односторонняя критическая область. Ясно, что при такой формулировке альтернативной гипотезы на основании экономических соображений должен быть априори известен знак параметра регрессии.
Для проверки гипотезы 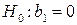 используется статистика
используется статистика
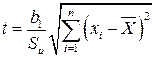 , (1.4)
, (1.4)
а гипотезы 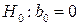 – статистика
– статистика
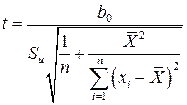 , (1.5)
, (1.5)
подчиняющиеся распределению Стьюдента с 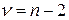 степенями свободы; а
степенями свободы; а 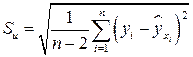 - стандартная ошибка регрессии.
- стандартная ошибка регрессии.
Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми экономическими явлениями. При этом выдвигаются следующие гипотезы:
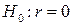 – между переменными X и Y отсутствует значимая корреляционная связь;
– между переменными X и Y отсутствует значимая корреляционная связь;
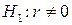 – между переменными Y и X имеется существенная корреляционная связь.
– между переменными Y и X имеется существенная корреляционная связь.
Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.
Для проверки гипотезы 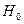 по результатам выборки используется статистика
по результатам выборки используется статистика
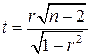 , (1.6)
, (1.6)
распределенная по закону Стьюдента с 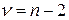 степенями свободы.
степенями свободы.
Вычисленные по результатам выборки статистики (1.4) – (1.6) сравниваются с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости 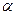 и
и 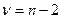 степенях свободы. Если
степенях свободы. Если 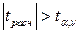 , то нулевая гипотеза
, то нулевая гипотеза 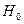 отвергается, т.е. корреляционно-регрессионная связь между переменными Y и X значима; если же
отвергается, т.е. корреляционно-регрессионная связь между переменными Y и X значима; если же 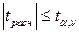 , то гипотеза об отсутствии связи не вызывает возражений, т.е. принимается гипотеза
, то гипотеза об отсутствии связи не вызывает возражений, т.е. принимается гипотеза 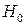 .
.
Дата добавления: 2015-08-20; просмотров: 1466;
