Парная регрессия и корреляция 1 страница
1.1.Понятие о функциональной, статистической и корреляционной зависимостях.Поведение и значение любого экономического показателя зависит от множества факторов, хотя только их ограниченное количество существенно воздействует на исследуемый экономический показатель. Выделение и учет в модели лишь ограниченного числа факторов оказывающих существенное влияние на развитие моделируемого экономического процесса, определение их взаимосвязи, являются ключевыми для принятия решений.
Остановимся вначале на изучении взаимосвязей между двумя переменными 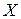 и
и 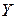 , составляющими двумерной случайной величины
, составляющими двумерной случайной величины 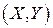 . Если каждому значению одной случайной величины по некоторому правилу относится одно значение другой случайной величины, то говорят о функциональной зависимости. В подавляющем большинстве случаев между экономическими переменными таких зависимостей нет. Это связано с целым рядом причин, поскольку при анализе влияния одной переменной на другую не учитывается ряд других факторов, влияющих на нее, и это влияние может быть не прямым, а косвенным и, кроме того, это влияние может носить случайный характер.
. Если каждому значению одной случайной величины по некоторому правилу относится одно значение другой случайной величины, то говорят о функциональной зависимости. В подавляющем большинстве случаев между экономическими переменными таких зависимостей нет. Это связано с целым рядом причин, поскольку при анализе влияния одной переменной на другую не учитывается ряд других факторов, влияющих на нее, и это влияние может быть не прямым, а косвенным и, кроме того, это влияние может носить случайный характер.
Зависимость между случайными величинами, имеющими общие случайные факторы, которые влияют как на одну, так и на другую случайную величину наряду с другими неодинаковыми для обеих случайных величин факторами, называется стохастической (вероятностной).
Так как при построении эконометрических моделей используются значения случайных величин (эмпирические значения), то стохастическую зависимость называют статистической.
Зависимость между исследуемыми случайными величинами называется статистической, если каждому эмпирическому значению одной случайной величины ( 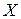 ) соответствует условное распределение эмпирических данных другой случайной величины (
) соответствует условное распределение эмпирических данных другой случайной величины ( 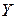 ).
).
На практике при обработке эмпирических данных 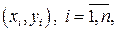 двумерной случайной величины
двумерной случайной величины 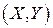 находят оценку регрессионной связи, т.е. оценку функции регрессии
находят оценку регрессионной связи, т.е. оценку функции регрессии 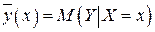 или
или 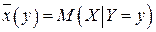 . Для этого используются эмпирические функции регрессии, содержащие случайную составляющую:
. Для этого используются эмпирические функции регрессии, содержащие случайную составляющую: 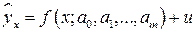 или
или 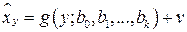 . Таким образом, регрессия – это односторонняя стохастическая зависимость между значениями одной случайной величины и условными математическими значениями другой случайной величины. Случайная составляющая подчеркивает факт не совпадения реальных значений с условными математическими ожиданиями этих значений.
. Таким образом, регрессия – это односторонняя стохастическая зависимость между значениями одной случайной величины и условными математическими значениями другой случайной величины. Случайная составляющая подчеркивает факт не совпадения реальных значений с условными математическими ожиданиями этих значений.
В зависимости от числа случайных величин, описывающих изучаемый экономический процесс, различают простую регрессию и множественную. Простая регрессия может быть положительной или отрицательной. При положительной регрессии с увеличением (уменьшением) независимой случайной величины увеличивается (уменьшается) зависимая случайная величина. При отрицательной регрессии – при увеличении (уменьшении) независимой случайной величины уменьшается (увеличивается) зависимая случайная величина.
По форме различают линейную регрессию и нелинейную, т.е. регрессию, выражаемую линейной и нелинейной функциями. В зависимости от типа соответствия между случайными величинами рассматривают непосредственную регрессию и косвенную. При непосредственной регрессии случайные величины связаны непосредственно друг с другом; при косвенной регрессии они детерминируются общей для них причиной.
Понятие регрессии тесно переплетается с понятием корреляции. Если в регрессионном анализе исследуется форма стохастической связи, то в корреляционном анализе оценивается интенсивность этой связи. Оба вида анализа служат для установления причинных соотношений между признаками изучаемых явлений и определения наличия или отсутствия связи между ними.
В зависимости от числа переменных величин, корреляция, может быть, простой (парной), или множественной. Корреляция между двумя случайными величинами называется простой, а между более чем двумя переменными – множественной. Корреляция между двумя переменными при фиксированном значении остальных переменных для случая множественной корреляции называется частной. Простая корреляция может быть положительной или отрицательной. Корреляция может быть линейной или нелинейной; непосредственной или косвенной.
1.2. Основные задачи прикладного корреляционно-регрессионного анализа.Построение качественного уравнения регрессии, наилучшим образом описывающего изучаемую зависимость, соответствующего эмпирическим данным и целям исследования, определяется следующими задачами:
- выбор формулы уравнения регрессии;
- определение параметров выбранного уравнения;
- нахождение точечных и интервальных оценок параметров функции регрессии;
- проверка адекватности построенной эмпирической функции регрессии эмпирическим данным.
Таким образом, основной задачей регрессионного анализа является подбор такой функции, которая бы наилучшим образом отражала экономическую закономерность, при помощи которой можно было бы решать задачи обоснованного прогноза.
Наряду с задачами регрессионного анализа решаются задачи корреляционного анализа:
- измерение интенсивности (силы, степени, тесноты) связи между факторами, описывающими изучаемый экономический процесс;
- отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями;
- обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждения об их наличии.
1.3. Выбор формы однофакторной регрессионной модели. Для более углубленного исследования связей и взаимозависимости экономических явлений математические методы, изученные в высшей математике, дополняются функциями регрессии, которые выражают количественное соотношение между факторным и результативным признаками. Форма связи между экономическими явлениями выражается аналитическим уравнением. При этом нужно определить такое математическое уравнение, которое наилучшим образом описывало бы характер исследуемого экономического процесса. Форму этой связи можно определить из расположения точек на корреляционном поле или из корреляционной таблицы, в которой вычисляются средние результативного признака для каждой группы факторного признака:
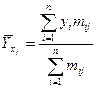 ,
,
где 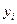 – значения середины интервалов ряда распределения Y;
– значения середины интервалов ряда распределения Y;  – частоты парных значений
– частоты парных значений 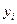 и
и  .
.
Для определения вида функции регрессии, используется также метод дисперсионного анализа, который позволяет оценивать линейность регрессии. Реализуем метод дисперсионного анализа для случая линейной формы связи: 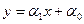 .
.
Сгруппируем всю совокупность наблюдений в виде таблицы:

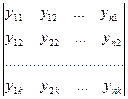
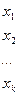 ,
,
где каждая строка соответствует определенному значению фактора X.
Для определения параметров 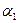 и
и 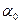 нужно минимизировать сумму
нужно минимизировать сумму
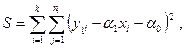
которую представим в виде

где 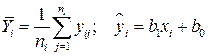 – эмпирическая линия регрессии. Это разложение приводит к дисперсиям:
– эмпирическая линия регрессии. Это разложение приводит к дисперсиям:
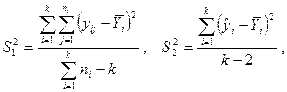
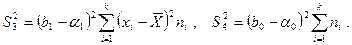
Дисперсии 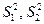 – это вариации значений признака соответственно в пределах групп наблюдений и около линии регрессии;
– это вариации значений признака соответственно в пределах групп наблюдений и около линии регрессии; 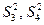 – вариации эмпирических коэффициентов по отношению к теоретическим коэффициентам.
– вариации эмпирических коэффициентов по отношению к теоретическим коэффициентам.
Для проверки гипотезы о линейности связи между исследуемыми признаками составляется F -отношение:
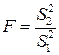 ,
,
которое подчиняется распределению Фишера – Снедокора с 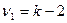 и
и 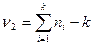 степенями свободы. Если вычисленное F-отношение меньше табличного для заданного уровня значимости
степенями свободы. Если вычисленное F-отношение меньше табличного для заданного уровня значимости 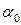 , то гипотеза о линейности связи подтверждается. Этот вывод следует из того, что если регрессия прямолинейная, то отклонения от нее следует считать случайными. Случайной при такой зависимости будет и та часть отклонений, которая приходится на различия между теоретической и эмпирической линиями регрессии. Теоретическая регрессия представляет то предельное положение, к которому стремится эмпирическая регрессия при увеличении числа наблюдений. Расхождение между ними обусловливается тем, что в эмпирической линии регрессии оказывается непогашенной некоторая часть случайных колебаний. Но это верно лишь тогда, когда теоретическая регрессия в виде прямой действительно правильно выражает форму связи. Если же это не так, то и отклонения эмпирической линии регрессии от теоретической прямой регрессии должны уже рассматриваться не как случайные, а как закономерное отражение кривизны регрессии. Сравнение этих отклонений с чисто случайной их величиной и должно дать ответ на поставленный вопрос о линейной регрессии.
, то гипотеза о линейности связи подтверждается. Этот вывод следует из того, что если регрессия прямолинейная, то отклонения от нее следует считать случайными. Случайной при такой зависимости будет и та часть отклонений, которая приходится на различия между теоретической и эмпирической линиями регрессии. Теоретическая регрессия представляет то предельное положение, к которому стремится эмпирическая регрессия при увеличении числа наблюдений. Расхождение между ними обусловливается тем, что в эмпирической линии регрессии оказывается непогашенной некоторая часть случайных колебаний. Но это верно лишь тогда, когда теоретическая регрессия в виде прямой действительно правильно выражает форму связи. Если же это не так, то и отклонения эмпирической линии регрессии от теоретической прямой регрессии должны уже рассматриваться не как случайные, а как закономерное отражение кривизны регрессии. Сравнение этих отклонений с чисто случайной их величиной и должно дать ответ на поставленный вопрос о линейной регрессии.
1.4. Основные предпосылки применения метода наименьших квадратов в аппроксимации связей признаков социально-экономических явлений (условия Гаусса – Маркова). Так как при построении регрессионной модели мы не можем охватить весь комплекс причин и учесть случайность, присущую в той или иной степени причинному действию и определяемому им следствию, то в выражение функции регрессии необходимо ввести аддитивную составляющую – возмущающую переменную U, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения Y можно вследствие этого представить в виде  . Для нахождения параметров расчетных значений Y должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
. Для нахождения параметров расчетных значений Y должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
Наиболее существенными предположениями являются следующие.
1. Полагаем, что для фиксированных значений переменных  математическое ожидание возмущающей переменной
математическое ожидание возмущающей переменной 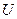 равно нулю:
равно нулю: 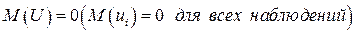 . Следовательно, средний уровень значений переменной Y определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
. Следовательно, средний уровень значений переменной Y определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
 .
.
2. Дисперсия случайной переменной U должна быть для всех значений 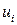 одинакова и постоянна:
одинакова и постоянна: 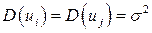 . Так как
. Так как 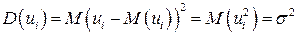 , то данную предпосылку можно переписать в виде:
, то данную предпосылку можно переписать в виде: 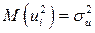 . Это свойство возмущающей переменной U называется гомоскедастичностью. Невыполнение данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
. Это свойство возмущающей переменной U называется гомоскедастичностью. Невыполнение данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
3. Значения случайной переменной U попарно независимы в вероятностном смысле: 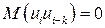 для
для 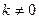 . Выполнимость данной предпосылки означает отсутствие систематической связи между любыми случайными отклонениями, т.е. об отсутствии автокорреляции.
. Выполнимость данной предпосылки означает отсутствие систематической связи между любыми случайными отклонениями, т.е. об отсутствии автокорреляции.
4. Число наблюдений должно превышать число параметров (n > m), иначе невозможна оценка этих параметров. Между факторными переменными не должно существовать строгой линейной зависимости, т.е. должна отсутствовать мультиколлинеарность между факторными переменными. При простой линейной регрессии это предположение сводится к условию 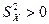 .
.
5. Переменные факторы 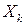 не должны коррелировать с возмущающей переменной U. Данное условие предполагает выполнимость соотношения
не должны коррелировать с возмущающей переменной U. Данное условие предполагает выполнимость соотношения
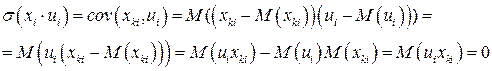 .
.
Это значит, что рассматривается односторонняя зависимость переменной Y от переменных  .
.
6. Возмущающая переменная распределена нормально. Предполагается, что переменная U не оказывает существенного влияния на переменную Y и представляет собой суммарный эффект от некоторого числа незначительных некоррелированных влияющих факторов.
Метод наименьших квадратов – один из наиболее распространенных методов оценивания неизвестных параметров регрессии по эмпирическим данным, хотя существуют и другие методы оценивания. Отметим, что при одних и тех же предположениях и одной и тои же функции регрессии различные способы оценивания приводят к разным оценкам параметров регрессии.
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между 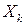 и Y в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии
и Y в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии 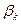 и их оценками
и их оценками 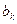 возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра
возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра 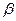 или что они являются несмещенными, состоятельными и эффективными.
или что они являются несмещенными, состоятельными и эффективными.
Состоятельность – важнейшее и минимально необходимое требование, предъявляемое к оценкам.
Если выполняются предпосылки 1 – 6, то оценки параметров регрессии, полученные методом наименьших квадратов, являются состоятельными, несмещенными и эффективными. Оценки, полученные методом наименьших квадратов, обладают наименьшей дисперсией. В этом смысле они представляют собой наилучшие линейные несмещенные оценки параметров теоретической регрессии. При нарушении предпосылок 2 и 3 нарушается свойство эффективности оценок, а свойства несмещенности и состоятельности сохраняется.
1.5. Построение регрессионной прямой методом наименьших квадратов. Если, исходя из профессионально-теоретических соображений в сочетании с исследованием расположения точек на корреляционном поле или других соображений, предполагают линейный характер зависимости усредненных значений результативного признака, то эту зависимость выражают с помощью функции линейной регрессии. Эта функция, называемая эмпирической регрессией, служит оценкой линейной функциональной связи между результативным и факторным признаками.
На результативный признак оказывает влияние и ряд других факторов. Чтобы элиминировать (сгладить) влияние этих факторов, нужно произвести выравнивание фактических величин Y на основании предположения, что между X и Y существует функциональная зависимость вида: 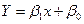 . При этом фактические значения Y заменяются значениями, вычисленными па формуле
. При этом фактические значения Y заменяются значениями, вычисленными па формуле
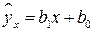 , (1.1)
, (1.1)
где  - оценка условного математического ожидания
- оценка условного математического ожидания 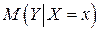 ,
, 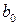 и
и 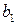 -
-
оценки неизвестных параметров 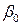 и
и 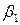 , называемые эмпирическими коэффициентами регрессии. В конкретном случае
, называемые эмпирическими коэффициентами регрессии. В конкретном случае
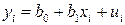 , (1.2)
, (1.2)
где отклонение 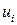 - оценка теоретического отклонения. Оценки
- оценка теоретического отклонения. Оценки 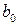 и
и 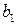 практически всегда отличаются от истинных значений коэффициентов
практически всегда отличаются от истинных значений коэффициентов 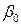 и
и 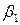 , что приводит к несовпадению эмпирической и теоретической линий регрессий.
, что приводит к несовпадению эмпирической и теоретической линий регрессий.
Так как все факторы, кроме фактора X, рассматриваются как постоянные средние величины и выражены параметрами 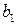 и
и 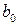 , то и сглаженные величины Y представляют собой средние
, то и сглаженные величины Y представляют собой средние 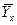 . Неизвестные параметры
. Неизвестные параметры 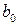 и
и 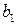 входящие в уравнение (1.1), определяются методом наименьших квадратов:
входящие в уравнение (1.1), определяются методом наименьших квадратов:
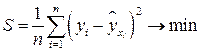 .
.
Величина S является функцией параметров 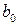 и
и 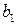 . Тогда, в силу необходимого условия экстремума, частные производные S по
. Тогда, в силу необходимого условия экстремума, частные производные S по 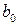 и
и 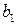 должны быть равны нулю:
должны быть равны нулю:
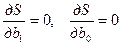 .
.
Выполнив преобразования и решив систему нормальных уравнений:
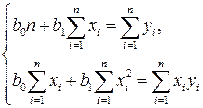 ,
,
получим:
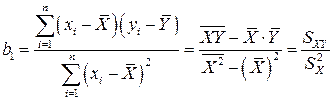 ,
, 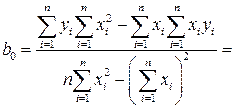
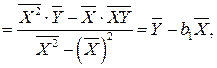
где
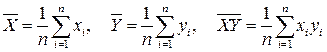 ,
, 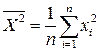 .
.
Оценки МНК являются: а) функциями от выборки (эмпирических данных); б) точечными оценками теоретических коэффициентов регрессии. Эмпирическая прямая регрессии проходит через точку 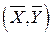 и среднее значений отклонений равно нулю
и среднее значений отклонений равно нулю 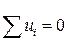 . Случайные отклонения
. Случайные отклонения 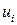 не коррелированны с наблюдаемыми значениями
не коррелированны с наблюдаемыми значениями 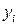 зависимой переменной
зависимой переменной 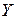 .
.
Параметр 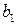 называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси Ox:
называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси Ox: 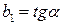 (рис. 1.1).
(рис. 1.1).
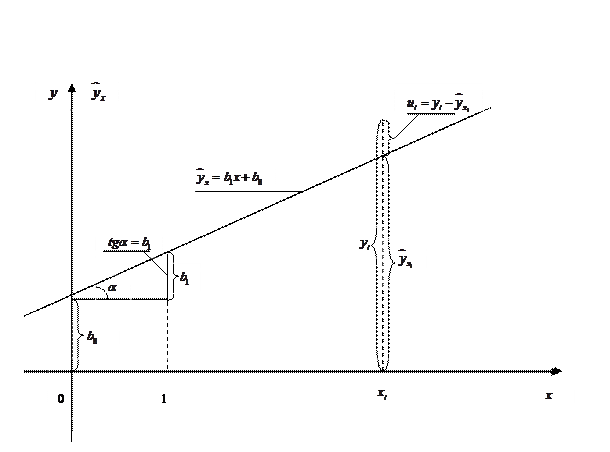
Рис.1.1
Коэффициент регрессии является мерой зависимости переменной Y от переменной X, т.е. 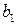 указывает, как в среднем изменяется значение переменной Y при изменении переменной X на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
указывает, как в среднем изменяется значение переменной Y при изменении переменной X на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
Отыскание значений коэффициента регрессии представляет большей практический интерес, если ставится вопрос о прогнозе изменений какого-либо показателя в связи с изменением того или иного условия. В частности, коэффициент регрессии используется для определения эластичности спроса и потребления.
В общем случае коэффициент эластичности представляет собой процентное изменение результативного признака при изменении факторного признака на один процент. Он вычисляется по формуле
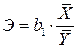 ,
,
где 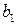 – коэффициент регрессии;
– коэффициент регрессии; 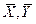 – средние значения соответственно факторного и результативного признаков.
– средние значения соответственно факторного и результативного признаков.
Например, коэффициент эластичности потребления выражает процентное изменение потребления или спроса на данный товар при изменении известных условий (дохода, цены и т.д.) на один процент.
Параметры 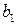 и
и 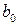 прямой регрессии – не безразмерные величины. Постоянная регрессии
прямой регрессии – не безразмерные величины. Постоянная регрессии 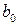 имеет размерность признака Y. Размерность коэффициента регрессии
имеет размерность признака Y. Размерность коэффициента регрессии 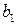 представляет собой отношение размерности результативного признака к размерности факторного признака.
представляет собой отношение размерности результативного признака к размерности факторного признака.
После вычисления оценок параметров регрессии 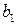 и
и 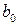 , а также средних значений
, а также средних значений 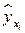 по формуле
по формуле 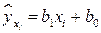 вычисляем остатки
вычисляем остатки
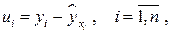
которые используются в качестве характеристики точности оценки регрессии или степени согласованности расчетных значений регрессии и наблюдаемых значений переменной Y. Для характеристики меры разброса фактических данных 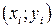 вокруг значений регрессии вычисляют дисперсию остатков:
вокруг значений регрессии вычисляют дисперсию остатков:
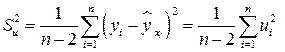 .
.
Геометрический смысл параметров прямой регрессии следует из рис. 1.1.
Используя дисперсию остатков, можно указать среднюю квадратичную ошибку коэффициента регрессии:
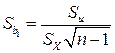 .
.
Кроме уравнения регрессии 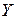 на
на 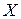 для тех же эмпирических данных может быть найдено уравнение регрессии
для тех же эмпирических данных может быть найдено уравнение регрессии 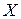 на
на 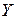 :
: 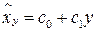 . Коэффициенты
. Коэффициенты 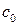 и
и 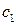 находятся по аналогичным формулам:
находятся по аналогичным формулам:
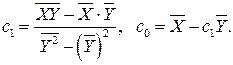
Как уже отмечалось, функция регрессии указывает, в какой степени изменяются значения результативного признака в соответствии с изменением факторного признака. Однако этого недостаточно для глубокого изучения их взаимосвязи. Нужно измерить еще интенсивность между изучаемыми факторами. Оценки, полученные с помощью уравнения регрессии, имеют точность тем большую, чем интенсивнее корреляция.
1.6. Измерение интенсивности линейной корреляционной связи. Мы рассмотрели, как определяется форма связи между факторным и результативным признаками. Изучим теперь показатели интенсивности этой связи.
При прямолинейной связи общим показателем интенсивности является линейный коэффициент корреляции (просто коэффициент корреляции)
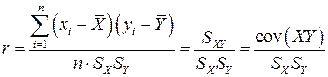 .
.
Коэффициент корреляции является безразмерной величиной, так как сравниваются не индивидуальные отклонения, а нормированные отклонения 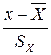 и
и  . Среднее произведение нормированных отклонений и дает коэффициент корреляции. Коэффициент корреляции удовлетворяет свойствам:
. Среднее произведение нормированных отклонений и дает коэффициент корреляции. Коэффициент корреляции удовлетворяет свойствам:
· Величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин 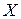 и
и 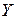 ;
;
· Коэффициент корреляции не превосходит по абсолютной величине единицы, т.е. 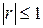 ;
;
· Коэффициент корреляции 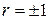 тогда и только тогда, когда между случайными величинами
тогда и только тогда, когда между случайными величинами 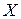 и
и 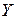 существует линейная функциональная зависимость;
существует линейная функциональная зависимость;
· Если между случайными величинами 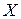 и
и 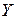 отсутствует хотя бы одна из корреляционных связей, то коэффициент корреляции равен нулю;
отсутствует хотя бы одна из корреляционных связей, то коэффициент корреляции равен нулю;
· Условие 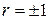 является необходимым и достаточным условием для совпадения регрессий
является необходимым и достаточным условием для совпадения регрессий 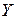 на
на 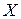 и
и 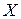 на
на 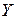 .
.
Степень интенсивности корреляционной связи можно определить из табл. 1.1.
Дата добавления: 2015-08-20; просмотров: 2015;
