В.2. Классификация математических методов и моделей
Математические модели социально-экономических явлений и процессов можно классифицировать так, как показано на рис. В.1.
| Эконометрические модели |
| Модели структуры | Модели взаимосвязи | Модели динамики | |||||||||||||||||||||||||||||||
| Группировки | Сходство Сходство | Кривые распределения | Уравнения регрессии | Система уравнений регрессии | Методы многомерной классификации | Трендовые | Периодических колебаний | Кривых роста | Многофакторные | ||||||||||||||||||||||||
Рис. В.1.
Модели структуры выражаются рядами и кривыми распределения. Модели структуры на основе группировок используются для изучения структуры народного хозяйства и его отраслей, для контроля за выполнением народнохозяйственных планов. Моделирование на основе группировок не связано с законами распределения и характеризует социально-экономические явления в «чистом» виде. Такие модели не позволяют делать количественные оценки, строить прогнозы, в них завуалированы тенденции развития социально-экономических явлений.
Модели структуры, выражающие сходство, строят с помощью мер близости (метрик), которые предполагают использование математического понятия расстояния (Евклидового, Хеммингова, Махаланобиса и т.д.). Меры близости позволяют выделять качественно однородные группы одновременно по большему числу признаков. Модели структуры, основанные на мерах близости (сходства), должны удовлетворять следующим условиям:
- эмпирические (наблюдаемые) данные в выделяемых подгруппах должны подчиняться нормальному (или близкому к нормальному) закону распределения;
- исходные данные должны быть выражены в одних и тех же единицах.
Модели структуры на основе кривых распределения характеризуют структуру социально-экономических явлений. Используя такие модели, можно сравнивать структуру социально-экономических явлений, имеющих различное происхождение, но относящихся к одному и тому же виду, и интерполировать распределение для значений, которые не были получены в результате наблюдений. Отметим, что выбор кривых распределения должен опираться на предварительный качественный анализ исследуемого явления. Кроме того, кривые распределения по возможности должны иметь более простое уравнение, и соответствующее уравнение должно содержать возможно меньшее число параметров.
Модели взаимосвязи описываются уравнениями регрессии. Построенное уравнение регрессии, проверенное на адекватность, становится статистической моделью, обладающей определенными прогнозными свойствами. Для учета всей системы сложных причинных связей и взаимосвязей результативных и факторных признаков строится регрессионная модель вида
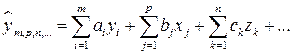
Такая модель может быть развернута в систему регрессионных уравнений, каждое из которых будет отражать одну из зависимостей исследуемого сложного объекта.
Все признаки, входящие в регрессионную модель, можно разделить на эндогенные и экзогенные. Эндогенные (результативные) признаки – это показатели, описываемые уравнениями модели. Их значения зависят от внутренней структуры объекта. Эндогенные признаки можно получить из решения системы. Экзогенные (факторные) признаки задаются извне и не зависят от структуры модели.
Если система разрешима относительно эндогенных показателей, то регрессионная модель сложного вида записывается в виде системы структурных уравнений:
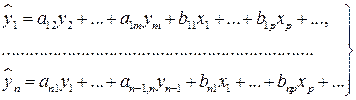
Модели динамики описываются функциями времени на основе трендовых моделей. Параметры трендовых моделей определяются методом наименьших квадратов. При этом предполагается, что тенденция, описываемая исходным динамическим рядом, остается неизменной. Динамический ряд образует числовая последовательность наблюдений 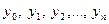 , характеризующих изменение экономического явления во времени, т.е. зарегистрированных в последовательные моменты времени
, характеризующих изменение экономического явления во времени, т.е. зарегистрированных в последовательные моменты времени 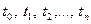 . Единственным независимым признаком в трендовых моделях является время
. Единственным независимым признаком в трендовых моделях является время 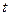 .
.
Многофакторное моделирование динамики осуществляется на основе связных рядов. Модель может быть выражена многофакторным уравнением регрессии, в котором время является дополнительным факторным признаком.
Для выявления главных черт моделей рассмотрим пример.
Пример В.1 (предложение и спрос на конкурентном рынке). Разделение труда в рыночных условиях сопровождается многочисленными обменами, благодаря которым производимые ценности распределяются по различным каналам. Каждый обмен – это результат свободного соглашения между продавцом и покупателем товара по согласованной между ними цене.
Пусть 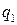 – запрашиваемые,
– запрашиваемые, 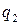 – предложенные количества какого-либо продукта в некоторый
– предложенные количества какого-либо продукта в некоторый  день на рынке, а
день на рынке, а 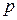 – цена, по которой заключаются сделки. Ясно, что
– цена, по которой заключаются сделки. Ясно, что 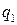 и
и 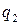 зависят от цены
зависят от цены 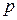 , так как участники рынка, совершающие сделки, решают не покупать или не продавать, если цена их не устраивает. Следовательно,
, так как участники рынка, совершающие сделки, решают не покупать или не продавать, если цена их не устраивает. Следовательно, 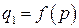 и
и 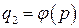 – функции спроса и предложения, которые определяют соответственно
– функции спроса и предложения, которые определяют соответственно 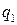 и
и 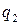 , если задана цена
, если задана цена 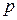 . Равновесие на рынке определяется равенством
. Равновесие на рынке определяется равенством 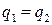 .
.
Итак, формально модель рынка устанавливает между тремя неотрицательными числовыми переменными 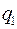 ,
, 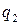 и
и 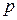 две зависимости:
две зависимости: 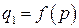 и
и 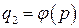 , где
, где 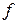 ,
, 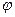 – заданные функции. Статистическая модель в случае равновесия имеет вид
– заданные функции. Статистическая модель в случае равновесия имеет вид
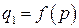 ,
, 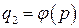 ,
, 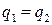 . (B.1)
. (B.1)
Эта модель отражает лишь зависимость предложения и спроса от цены данного продукта, хотя в действительности они в различной степени зависят от множества цен и системы снабжения в рассматриваемой экономической системе. Поэтому модель вида (В.1) можно записать так:
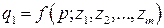 ,
, 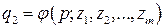 ,
, 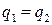 . (B.2)
. (B.2)
Здесь функции 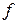 и
и 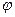 зависят от стольких переменных, сколько их требуется для достаточно адекватного представления факторов, влияющих на предложение и спрос.
зависят от стольких переменных, сколько их требуется для достаточно адекватного представления факторов, влияющих на предложение и спрос.
Модели (В.1) и (В.2) предполагают мгновенную адаптацию предложения и спроса при изменениях цен в связи с тем, что в них не учитывается влияние времени. Если же предложение и спрос зависят от времени года, то предпочтительнее следующая модель:
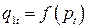 ,
, 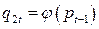 ,
, 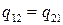 , (B.3)
, (B.3)
в которой цена 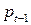 года
года 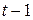 определяет предложение года
определяет предложение года 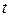 .
.
Необходимое равновесие сделок и форма закона спроса фиксируют цену 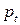 года
года 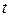 , которая определяет предложение
, которая определяет предложение 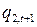 года
года 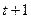 , и т.д. Модель (В.3) называют «паутинной моделью». Так, если на ось абсцисс нанести цены, а на ось ординат – количества, то кривая спроса
, и т.д. Модель (В.3) называют «паутинной моделью». Так, если на ось абсцисс нанести цены, а на ось ординат – количества, то кривая спроса 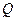 (график функции
(график функции 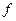 ) и кривая предложения
) и кривая предложения  (график функции
(график функции 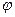 ) будут иметь вид, показанный на рис. В.2.
) будут иметь вид, показанный на рис. В.2.
Если цена равна 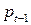 , то точка
, то точка 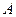 на кривой предложения
на кривой предложения  определяет
определяет 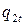 , равное
, равное 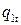 . Соответствующая точка
. Соответствующая точка 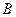 на кривой спроса
на кривой спроса 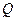 определяет
определяет 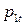 .
.

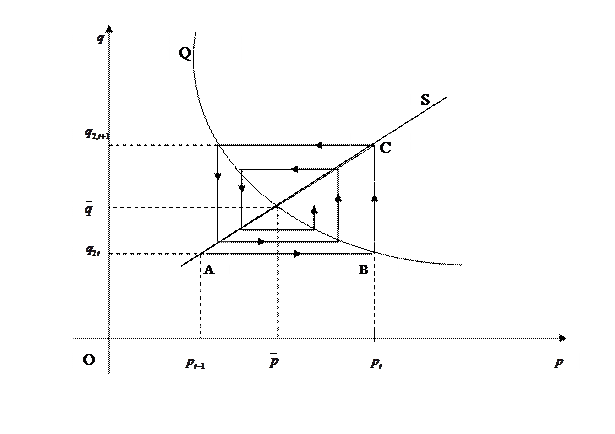
Рис. В.2
Точка 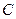 на кривой предложения
на кривой предложения  определяет
определяет 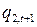 и т.д. Двигаясь по ломаной спирали, находим цену, спрос и предложение. Ясно, что в зависимости от вида кривых
и т.д. Двигаясь по ломаной спирали, находим цену, спрос и предложение. Ясно, что в зависимости от вида кривых 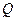 и
и  ломаная линия
ломаная линия 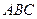 ..., имеющая вид паутины, может сходиться к точке равновесия модели (В.3) или нет.
..., имеющая вид паутины, может сходиться к точке равновесия модели (В.3) или нет.
Рассмотренная модель взята из экономической теории и достаточно хорошо иллюстрирует характерные общие формы модели. Из этой модели видно, какие логические проблемы возникают при изучении фактических данных.
Дата добавления: 2015-08-20; просмотров: 1048;
