Парная регрессия и корреляция 6 страница
Если принимается гипотеза  , то вычисляется свободная оценка коэффициента регрессии по формуле
, то вычисляется свободная оценка коэффициента регрессии по формуле
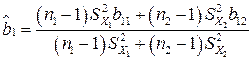 . (2.23)
. (2.23)
Если принимаются гипотезы о равенстве дисперсий остатков и коэффициентов регрессий, то оценивается расхождение свободных членов в двух сравниваемых уравнениях регрессии. Для этого выдвигается нулевая гипотеза  , состоящая в том, что свободные члены
, состоящая в том, что свободные члены 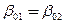 , против альтернативной гипотезы
, против альтернативной гипотезы 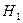 :
: 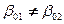 . Проверку нулевой гипотезы
. Проверку нулевой гипотезы  осуществляем с помощью статистики
осуществляем с помощью статистики
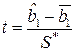 , (2.24)
, (2.24)
имеющей t-распределение с 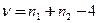 степенями свободы. В статистике (2.24)
степенями свободы. В статистике (2.24) 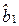 - сводная оценка коэффициента регрессии (2.23),
- сводная оценка коэффициента регрессии (2.23), 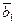 - оценка углового коэффициента для двух уравнений регрессии, полученная по формуле
- оценка углового коэффициента для двух уравнений регрессии, полученная по формуле
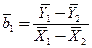
в предположении равенства как коэффициентов регрессии, так и свободных членов. Индекс в обозначениях средних соответствует номеру выборки. В формуле (2.24) стандартное отклонение
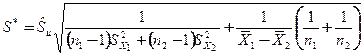 ,
,
где 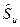 определяется по формуле (2.21). Определив квантиль
определяется по формуле (2.21). Определив квантиль 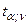 для уровня значимости
для уровня значимости 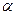 при
при 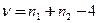 степенях свободы, сравним его с
степенях свободы, сравним его с 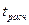 , найденным по формуле (3.24). Если
, найденным по формуле (3.24). Если 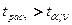 , то постоянные регрессии существенно отличаются друг от друга на уровне значимости
, то постоянные регрессии существенно отличаются друг от друга на уровне значимости 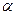 . В этом случае прямые регрессии не идентичны, так как имеется статистически значимое расхождение постоянных. Если же
. В этом случае прямые регрессии не идентичны, так как имеется статистически значимое расхождение постоянных. Если же 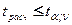 , то обе регрессионные прямые считаются идентичными, а имеющиеся различия между ними можно объяснить лишь случайными колебаниями выборочных данных.
, то обе регрессионные прямые считаются идентичными, а имеющиеся различия между ними можно объяснить лишь случайными колебаниями выборочных данных.
Таким образом, если на всех трех этапах принимаются нулевые гипотезы, то полученная форма усредненной зависимости может быть принята для обеих генеральных совокупностей.
Проверку гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений (выборок) можно осуществить также при помощи теста Чоу, который состоит в следующем.
Пусть для двух выборок объемами 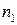 и
и 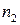 построены два уравнения регрессии
построены два уравнения регрессии
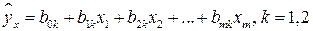 .
.
Проверим гипотезу 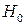 , состоящую в том, что соответствующие коэффициенты регрессии равны:
, состоящую в том, что соответствующие коэффициенты регрессии равны: 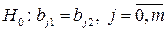 . Обозначим
. Обозначим 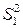 и
и 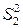 дисперсии остатков для первого и второго уравнений регрессии. Пусть для объединенной выборки объема
дисперсии остатков для первого и второго уравнений регрессии. Пусть для объединенной выборки объема 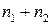 построено еще одно уравнение регрессии, для которого дисперсия остатков равна
построено еще одно уравнение регрессии, для которого дисперсия остатков равна 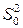 . Для проверки гипотезы
. Для проверки гипотезы 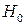 применяется
применяется 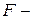 статистика:
статистика:
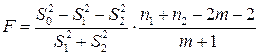 ,
,
подчиняющаяся 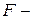 распределению с числом степеней свободы
распределению с числом степеней свободы 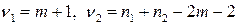 . Тогда если
. Тогда если  , то принимается гипотеза
, то принимается гипотеза 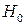 . Это означает, что уравнения регрессии для обеих выборок практически одинаковы. Если же
. Это означает, что уравнения регрессии для обеих выборок практически одинаковы. Если же 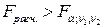 , то нулевая гипотеза
, то нулевая гипотеза 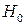 отклоняется, что свидетельствует о различии уравнений регрессии с вероятностью
отклоняется, что свидетельствует о различии уравнений регрессии с вероятностью 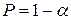 .
.
2.7. Проверка выполнимости предпосылок МНК. Статистика Дарбина – Уотсона.Статистическая значимость коэффициентов регрессии и близкое значение коэффициента детерминации 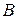 к единице не гарантируют высокое качество уравнения регрессии, поскольку могут нарушаться предпосылки МНК (п. 1.4). Нарушение необходимых предпосылок влияет на точность оценок коэффициентов регрессии, увеличивая их стандартные ошибки, и обычно свидетельствует о неверной спецификации самого уравнения.
к единице не гарантируют высокое качество уравнения регрессии, поскольку могут нарушаться предпосылки МНК (п. 1.4). Нарушение необходимых предпосылок влияет на точность оценок коэффициентов регрессии, увеличивая их стандартные ошибки, и обычно свидетельствует о неверной спецификации самого уравнения.
При построении линейного уравнения регрессии, мы предполагаем, что реальная взаимосвязь факторных признаков с результативным признаком является линейной, отклонения от линии регрессии являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности, эффективности и состоятельности, и анализ их значимости будет не точным. Указанные предположения могут не выполняться вследствие нелинейности изучаемой зависимости или при наличии существенного неучтенного фактора в модели. Поэтому на начальном этапе проверяется, как правило, выполнимость статистической независимости оценок отклонений 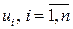 , между собой. Для этого проверяется коррелированность соседних отклонений
, между собой. Для этого проверяется коррелированность соседних отклонений 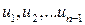 и
и 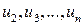 , используя коэффициент автокорреляции первого порядка:
, используя коэффициент автокорреляции первого порядка:
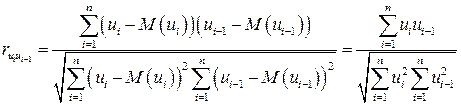 ,(2.25)
,(2.25)
где математическое ожидание 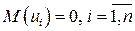 . На практике для анализа коррелированности отклонений вычисляют статистику Дарбина - Уотсона:
. На практике для анализа коррелированности отклонений вычисляют статистику Дарбина - Уотсона:
 ,(2.26)
,(2.26)
которая связана с коэффициентом автокорреляции равенством 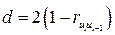 . Можно показать, что необходимым условием независимости случайных отклонений является близость к двойке статистики Дарбина – Уотсона:
. Можно показать, что необходимым условием независимости случайных отклонений является близость к двойке статистики Дарбина – Уотсона: 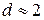 . В этом случае считается, что отклонения от регрессии являются случайными и что построенная линейная регрессия, вероятно, отражает реальную зависимость. Для ответа на вопрос, какие значения
. В этом случае считается, что отклонения от регрессии являются случайными и что построенная линейная регрессия, вероятно, отражает реальную зависимость. Для ответа на вопрос, какие значения 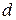 можно считать близкими к двум, разработаны таблицы критических значений статистики Дарбина – Уотсона. В таблице, по данному числу наблюдений
можно считать близкими к двум, разработаны таблицы критических значений статистики Дарбина – Уотсона. В таблице, по данному числу наблюдений 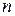 , количеству факторов
, количеству факторов 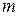 и заданному уровню значимости
и заданному уровню значимости 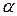 , определяются два числа:
, определяются два числа: 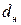 - нижняя граница и
- нижняя граница и 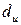 - верхняя граница, которые устанавливают границы приемлемости расчетной статистики
- верхняя граница, которые устанавливают границы приемлемости расчетной статистики 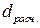 .
.
Если 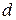 <
< 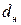 , то существует положительная автокорреляция остатков;
, то существует положительная автокорреляция остатков;
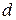 > 4
> 4 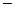
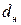 , то существует отрицательная автокорреляция остатков;
, то существует отрицательная автокорреляция остатков;
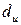 <
< 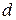 < 4
< 4 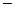
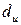 , то автокорреляция остатков отсутствует;
, то автокорреляция остатков отсутствует;
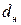 <
< 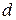 <
< 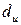 или 4
или 4 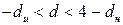 , то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
При наличии автокорреляция остатков уравнение регрессии считается неудовлетворительным.
Заметим, что если выполняется неравенство 1,5 <  , то можно приближенно считать, что автокорреляция остатков отсутствует.
, то можно приближенно считать, что автокорреляция остатков отсутствует.
2.8. Оценка адекватности многофакторной регрессионной модели. После оценки надежности всех параметров уравнения множественной регрессии и статистической независимости отклонений важной является оценка адекватности уравнения регрессии в целом. Ее проводят с помощью методики, изложенной в п. 1.9. По значению коэффициента корреляции R также можно судить об адекватности уравнения регрессии изучаемому экономическому процессу. При 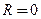 следует считать модель полностью неадекватной; при R = 1 уравнение регрессии в общем и целом воспроизводит свойства исследуемого экономического процесса.
следует считать модель полностью неадекватной; при R = 1 уравнение регрессии в общем и целом воспроизводит свойства исследуемого экономического процесса.
По коэффициенту множественной корреляции можно судить, достаточно ли выбранные переменные 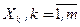 , обусловливают количественную вариацию зависимой переменной, так как
, обусловливают количественную вариацию зависимой переменной, так как
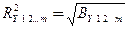 ,
,
а коэффициент детерминации устанавливает долю дисперсии, которая обусловлена воздействием изменений объясняющих переменных.
Перечислим показатели, характеризующие качество регрессионных моделей.
1. Средний квадрат ошибок регрессионной модели
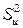 =
= 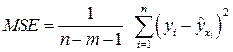 .
.
Выбор формы модели обычно производится именно по этому показателю. Он должен быть минимальным.
2. Коэффициент аппроксимации МАРЕ. Он характеризует адекватность модели реальному распределению значений анализируемого показателя:
 .
.
Если МАРЕ < 10 %, модель имеет высокую точность, если 10 % < МАРЕ < 20 %, модель имеет хорошую точность (допустимую). При 20 % < МАРЕ < 50 % точность модели удовлетворительная. Использование такой модели на практике спорно. Если МАРЕ > 50 %, то точность модели неудовлетворительная и ее использование в анализе недопустимо.
3. F-критерий Фишера. Он характеризует соотношение квадратов значений результативного признака и квадратов ошибки модели:
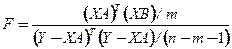 ,
,
где 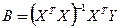 ; m - число оцениваемых параметров; n - число наблюдений. Критерий
; m - число оцениваемых параметров; n - число наблюдений. Критерий  сравнивается с
сравнивается с 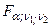 при
при 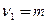 и
и  степенях свободы. Если
степенях свободы. Если 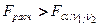 , то адекватность модели в целом подтверждается. В анализе F-критерий Фишера используется довольно часто. Оценки, полученные на его основе, как правило, достаточно надежны.
, то адекватность модели в целом подтверждается. В анализе F-критерий Фишера используется довольно часто. Оценки, полученные на его основе, как правило, достаточно надежны.
2.9. Построение многофакторной регрессионной модели. В качестве объекта анализа были исследованы четыре предприятия легкой (швейной) промышленности Гродненской области. Исходные данные взяты из статистического сборника, из раздела “Основные показатели работы промышленности Гродненской области по данным годовых отчетов за 1990 г.”, а также из отчетностей по форме Iс (годовая) за январь - декабрь 1990 г., отчетности предприятия (объединения) по труду. Данные внесены в табл. 2.1.
Т а б л и ц а 2.1
| Номер пред-прия- тия | Среднегодовая выработка продукции предприятия на 1 одного
работающего 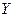 ,
тыс. р. ,
тыс. р.
| Фондоотдача 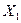 , тыс. р. , тыс. р.
| Фондо-
вооружённость
 , тыс. р. , тыс. р.
|
| 31,2 28,2 24,6 9,4 | 6,69 11,54 6,33 3,77 | 4,66 2,44 3,88 2,51 |
Задача состоит в нахождении аналитического выражения, наилучшим образом отражающего связь факторных признаков (фондоотдачи 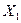 и фондовооруженности
и фондовооруженности  ) с результативным (производительностью труда Y), т.е. в нахождении функции
) с результативным (производительностью труда Y), т.е. в нахождении функции 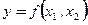 . Решение этой задачи позволяет раскрыть механизм управления изучаемым показателем.
. Решение этой задачи позволяет раскрыть механизм управления изучаемым показателем.
Эмпирическое обоснование типа функции с помощью графического анализа парных связей в случае однофакторных моделей практически непригодно для многофакторной модели. Выбор типа функции может опираться на теоретическое обоснование изучаемого явления.
Анализ табл. 2.20 позволяет сделать вывод, что между изучаемыми показателями существует линейная зависимость вида
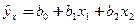 .
.
Параметры 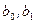 и
и 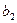 этой функции регрессии найдем из системы нормальных уравнений
этой функции регрессии найдем из системы нормальных уравнений
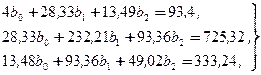
решив которую, получим: 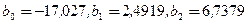 . Тогда уравнение множественной регрессии, выражающее зависимость производительности труда Y от фондоотдачи
. Тогда уравнение множественной регрессии, выражающее зависимость производительности труда Y от фондоотдачи 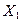 и фондовооруженности
и фондовооруженности  , будет иметь вид
, будет иметь вид
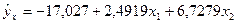 .
.
На основании уравнения множественной регрессии был сделан следующий вывод: при увеличении уровня фондоотдачи и фондовооруженности производства на одну единицу производительность труда в среднем возрастает соответственно на 2,49 и 6,74 тыс. р.
Парные коэффициенты корреляции равны:
 .
.
Достаточно высокие значения коэффициентов корреляции 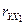 и
и 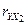 свидетельствуют о заметной корреляционной связи фондоотдачи и фондовооруженности с производительностью труда. Между факторами
свидетельствуют о заметной корреляционной связи фондоотдачи и фондовооруженности с производительностью труда. Между факторами 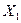 и
и  корреляционная связь обратная.
корреляционная связь обратная.
Частные коэффициенты корреляции, которые являются мерой тесноты линейной корреляционной зависимости между случайными величинами Y и 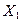 при исключении или фиксировании случайной величины
при исключении или фиксировании случайной величины  либо Y и
либо Y и  при исключении или фиксировании случайной величины
при исключении или фиксировании случайной величины 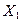 , равны:
, равны:
 .
.
Анализ значений частных и парных коэффициентов регрессии показывает, что наибольшее влияние на результативный признак Y - производительность труда - оказывает фактор  - фондовооруженность.
- фондовооруженность.
В связи с тем, что надежность коэффициентов корреляции зависит от объема выборки, а объем выборки в нашем примере весьма мал, и так как построение модели носит иллюстративный характер, процедуру проверки существенности статистических характеристик рассмотрим в следующем примере.
Для выявления тесноты связи результативного показателя с обоими факторами одновременно вычислим коэффициент множественной корреляции:
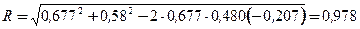 .
.
Значение коэффициента множественной корреляции свидетельствует о весьма тесной корреляционной зависимости фактора Y и факторов 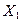 и
и  . Его средня квадратичная ошибка незначительна:
. Его средня квадратичная ошибка незначительна:
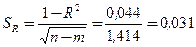 .
.
Так как 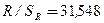 , с веротностью 0,99 можно считать R существенным.
, с веротностью 0,99 можно считать R существенным.
Совокупный коэффициент множественной детерминации 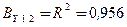 . Он показывает, что вариация производительности труда на 95,6 % обусловливается двумя выделенными факторами и лишь 4,4 % общей дисперсии не может быть объяснено этой зависимостью. Значит, выбранные факторы существенно влияют на показатель производительности труда, а уравнение регрессии статистически значимо, его подбор выполнен хорошо. Таким образом, изученная с помощью многофакторного корреляционного анализа статистическая связь между исследуемыми показателями свидетельствует о целесообразности построения двухфакторной регрессионной модели.
. Он показывает, что вариация производительности труда на 95,6 % обусловливается двумя выделенными факторами и лишь 4,4 % общей дисперсии не может быть объяснено этой зависимостью. Значит, выбранные факторы существенно влияют на показатель производительности труда, а уравнение регрессии статистически значимо, его подбор выполнен хорошо. Таким образом, изученная с помощью многофакторного корреляционного анализа статистическая связь между исследуемыми показателями свидетельствует о целесообразности построения двухфакторной регрессионной модели.
Вычислим далее частные коэффициенты эластичности 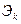 и
и 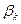 -коэффициенты.
-коэффициенты.
Коэффициент эластичности показывает, насколько изменяется результативный признак (в процентах) при изменении факторного признака на 1 %:
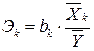 ,
,
где 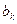 - коэффициент регрессии при k-м факторе;
- коэффициент регрессии при k-м факторе; 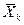 - среднее значение k-го фактора;
- среднее значение k-го фактора; 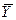 - среднее значение изучаемого показателя. Находим:
- среднее значение изучаемого показателя. Находим:
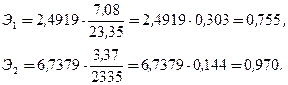
Анализ частных коэффициентов эластичности 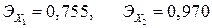 показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор
показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор  - фондовооруженность. Увеличение фондовооруженности на 1 % дает прирост производительности труда на 97 %. Увеличение фондоотдачи на 1 % приводит к повышению производительности труда на 75,5 %.
- фондовооруженность. Увеличение фондовооруженности на 1 % дает прирост производительности труда на 97 %. Увеличение фондоотдачи на 1 % приводит к повышению производительности труда на 75,5 %.
Бета-коэффициент отражает скорость изменения среднего значения функции Y по каждому из факторов при постоянном значении остальных.
Вычислим 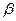 - коэффициенты по формуле
- коэффициенты по формуле
 ,
,
где 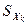 ,
, 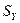 - средние квадратичные отклонения величин
- средние квадратичные отклонения величин 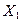 ,
,  , Y;
, Y;
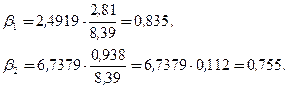
Анализ 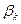 -коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их колеблемости способен оказать фактор
-коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их колеблемости способен оказать фактор 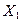 - фондоотдача, так как ему соответствует наибольшее (по абсолютной величине) значение
- фондоотдача, так как ему соответствует наибольшее (по абсолютной величине) значение 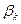 -коэффициента.
-коэффициента.
Таким образом, на основании частных коэффициентов эластичности 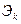 и
и 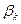 -коэффициентов можно судить о резервах предприятия, которые заложены в том или ином факторе.
-коэффициентов можно судить о резервах предприятия, которые заложены в том или ином факторе.
Средняя абсолютная процентная ошибка аппроксимации
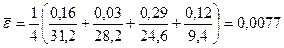
свидетельствует о том, что построенное уравнение множественной регрессии адекватно исследуемому влиянию отобранных факторов 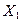 ,
,  на Y
на Y 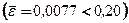 .
.
Адекватность модели изучаемому экономическому процессу подтверждают и значения коэффициентов множественной корреляции 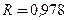 и детерминации
и детерминации 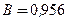 .
.
Определим общую дисперсию  остаточную дисперсию
остаточную дисперсию 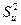 и
и 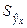 - дисперсию вследствие регрессии:
- дисперсию вследствие регрессии:
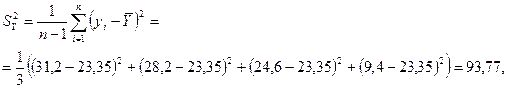
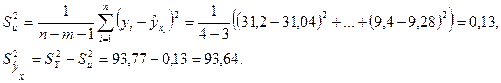
Вычислим критерий дисперсионного анализа:
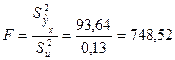 .
.
Из таблицы F-распределения Фишера с 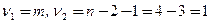 степенями свободы для заданного уровня значимости
степенями свободы для заданного уровня значимости 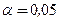 находим критическое значение
находим критическое значение 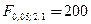 . Так как
. Так как 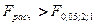 , то с веротностью P = 0,95 гипотеза
, то с веротностью P = 0,95 гипотеза  о нелинейности уравнения регрессии отвергается. Тем самым подтверждается адекватность уравнения регрессии исследуемому экономическому процессу.
о нелинейности уравнения регрессии отвергается. Тем самым подтверждается адекватность уравнения регрессии исследуемому экономическому процессу.
Сложность и взаимное переплетение отдельных факторов, обусловливающих исследуемое экономическое явление, может проявляться в линейной связи между всеми или некоторыми объясняющими переменными. Это явление носит название мультиколлинеарность. Под мультиколлинеарностью понимается наличие в уравнении регрессии более одной связи между объясняющими переменными (факторами). Причина заключается в том, что вариации в исходных данных перестают быть независимыми и поэтому невозможно выделить воздействие каждой объясняющей переменной в отдельности на зависимую переменную. Функциональная форма мультиколлинеарности возникает, когда по крайней мере одна из объясняющих переменных связана с другими объясняющими переменными линейным функциональным соотношением. Линейный коэффициент корреляции между этими двумя переменными в таком случае равен +1 или -1.
Исследуем, существует ли коллинеарность между 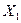 и
и  . Для проверки этого факта рассмотрим коэффициент корреляции
. Для проверки этого факта рассмотрим коэффициент корреляции 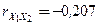 и оценим его значимость с помощью t-статистики:
и оценим его значимость с помощью t-статистики:
 .
.
Критическое значение, определенное по таблице распределения Стьюдента при заданном уровне значимости 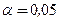 и
и 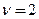 степенях свободы,
степенях свободы, 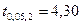 (двусторонняя критическая область). Так как
(двусторонняя критическая область). Так как 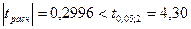 , то между переменными отсутствует значимая корреляционная связь. Кроме того, коэффициент парной корреляции
, то между переменными отсутствует значимая корреляционная связь. Кроме того, коэффициент парной корреляции 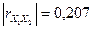 значительно меньше 0,8.
значительно меньше 0,8.
Проверку существования мультиколлинеарности проведем еще с помощью метода Фаррара - Глаубера. Для этого вычислим значение статистики:
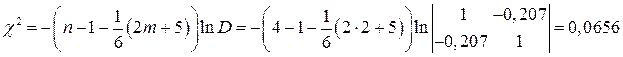 .
.
Критическое значение 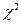 для доверительной вероятности 0,95 и
для доверительной вероятности 0,95 и 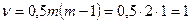 степеней свободы
степеней свободы 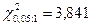 . Так как
. Так как 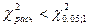 , то считаем, что мультиколлинеарность между объясняющими переменными на уровне значимости
, то считаем, что мультиколлинеарность между объясняющими переменными на уровне значимости 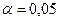 отсутствует.
отсутствует.
Итак, построенное уравнение регрессии адекватно отражает зависимость производительности труда от фондоотдачи и фондовооруженности.
Так как коэффициенты регрессии 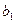 и
и 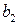 положительны, повышения производительности труда Y можно добиться, увеличив показатели
положительны, повышения производительности труда Y можно добиться, увеличив показатели 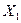 и
и  . При этом следует учитывать, что на эффективность производства оказывает влияние не только производительность труда, но и другие факторы
. При этом следует учитывать, что на эффективность производства оказывает влияние не только производительность труда, но и другие факторы
Дата добавления: 2015-08-20; просмотров: 1961;
