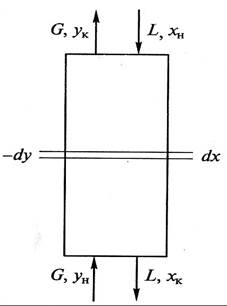
Материальный баланс

Таким образом, переданное количество dМ распределяемого компонента можно записать как по одной, таки по другой распределяющим фазам:

Уравнение (9.2) является дифференциальным уравнением материального баланса массообменного процесса.

Для получения полного (интегрального) уравнения материального баланса проинтегрируем его в пределах изменения рабочих концентраций

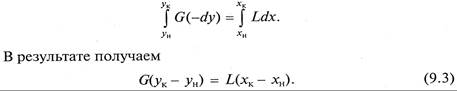
Легко убедиться, что уравнение (9.3), так же как и (9.2), не зависит от направления движения взаимодействующих фаз, а характеризует только материальный баланс системы при массопередаче.

Важной характеристикой массоо6менных процессов являются уравнения рабочих линий, которые связывают между собой концентрации распределяемого компонента в распределяющих фазах во время осуществления процесса.

Различают два основных способа взаимодействия распределяющих фаз в процессе массообмена: противоток и прямоток.

1. Противоточная схема проведения процесса массопередачи (рис. 9.2, а).

Используя уравнение материального баланса (9.2), проинтегрируем его для верхней части аппарата в указанных на схеме пределах:

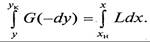
В результате получаем уравнение рабочей линии противоточного процесса массопередачи

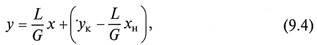
которое является уравнением прямой с тангенсом угла наклона L/G. Второе слагаемое является постоянной величиной, Не меняющейся в случае интегрирования уравнения (9.2) в пределах концентраций в нижней части массообменного аппарата.

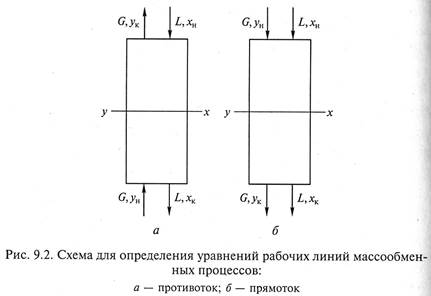
2. Прямоточная схема осуществления процесса массопередачи (рис. 9.2, б).

Интегрирование уравнения (9.2) произведем также для верхней части массообменного аппарата в указанных на схеме пределах:

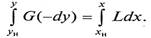
В результате получаем уравнение рабочей линии прямоточного процесса массопередачи

Уравнение (9.5) также является уравнением прямой линии, однако угол наклона этой прямой противоположен углу наклона рабочей линии противоточного массообменного процесса, о чем указывает знак « - » перед значением тангенса угла (L/G) наклона прямой.

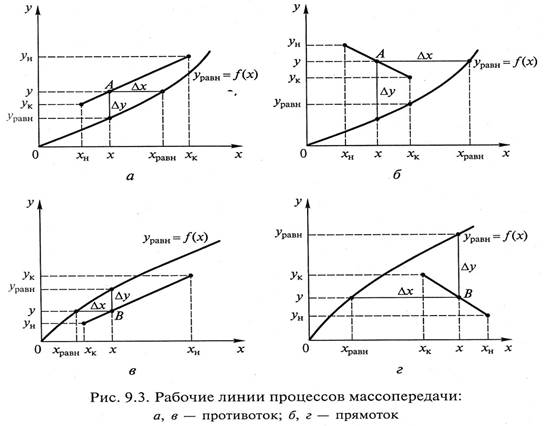
Изображения рабочих линий процесса массопередачи для противотока и прямотока представлены на рис. 9.3.

Движущая сила массоо6менного процесса определяется степенью отклонения системы от равновесия и может быть выражена разностью содержаний целевого компонента в рабочем и равновесном состояниях системы (Δу или Δх). Направление переноса

распределяемого вещества удобно определять на диаграмме у – х по расположению равновесной и рабочей линий.

Если рабочая линия расположена выше линии равновесия (рис. 9.3, а, б), то для любой точки, расположенной на этой линии (точка А), у > у_равн и х < х_равн, где у_равн и х_равн – равновесные составы фаз, соответствующие текущим концентрациям у и х. В этом случае распределяемое вещество будет переходить из фазы G в фазу L, а движущая сила в точке А составит Δу = у – у_равн (по фазе G) и Δх = х_равн – х (по фазе L).

Если рабочая линия расположена ниже линии равновесия (рис. 9.3, в, г), то для произвольно выбранной точки В концентрации y < у_равн и х > х_равн.

При таком процессе распределяемый компонент будет переходить из фазы L в фазу G, причем движущая сила в точке В, выраженная через концентрации соответствующих фаз, может быть записана как Δу = у_равн – y и Δх = х – х_равн.

Скорость массопередачи может быть выражена через количество вещества, переходящего в единицу времени из одной фазы в другую. В этом случае, в соответствии с (В. 3) можно записать основное уравнение массопередачи в дифференциальном

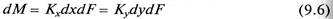
или интегральном (для стационарных процессов) виде

Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах, между которыми происходит массообмен.

Перенос вещества в фазах может происходить либо путем молекулярной диффузии, либо конвекцией и молекулярной диффузией одновременно (конвективная диффузия).

Массопередача молекулярной диффузией осуществляется в неподвижной среде вследствие движения молекул, атомов и ионов.

Массопередача конвективной диффузией реализуется в движущейся среде. При этом если движение жидкости обусловлено градиентами температуры или концентрацией, то такая конвекция называется свободной, или естественной. Если движение вызвано внешними силами, конвекция является вынужденной.

В случае турбулентного движения жидкости, сопровождающегося массопередачей, в ряде случаев рассматривают турбулентный механизм переноса вещества, при котором оно переносится беспорядочными турбулентными пульсациями потока. Такой механизм называется турбулентной диффузией.

Молекулярная диффузия описывается первым законом Фика, в соответствии с которым количество продиффундировавшего вещества dМ пропорционально градиенту концентрации в направлении диффузии дс/дп, площади массопередачи dF, перпендикулярной направлению диффузионного потока и времени осуществления процесса dτ,

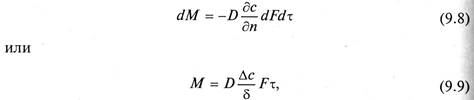
где 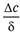- изменение концентрации вещества по толщине слоя δ.

Коэффициент пропорциональности D в уравнениях (9.8) и (9.9) называется коэффициентом молекулярной диффузии и имеет размерность м²/с при с, кг/м³.

Коэффициент молекулярной диффузии показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице. Значение коэффициента молекулярной диффузии зависит от природы и свойств как распределяемого вещества, таки среды, через которую он диффундирует, а также давления и температуры. Причем увеличению его значения способствует повышение температуры и уменьшение давления. Знак минус перед правой частью уравнения (9.8) указывает на то, что молекулярная диффузия протекает в направлении уменьшения концентрации распределяемого компонента.

В ряде случаев по аналогии с первым законом Фика, записывают уравнение, характеризующее массопередачу в результате турбулентной диффузии,

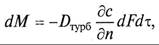
где D_турб – коэффициент турбулентной диффузии, зависящий от гидродинамических условий протекания процесса — скорости потока и масштаба турбулентных пульсаций.

Конвективная диффузия характеризуется тем, что полный поток вещества складывается из конвективного и диффузионного потоков.

Поскольку конвективный перенос вещества осуществляется преимущественно потоками жидкости, его интенсивность учитывается компонентами скорости перемещения массы, диффузионная составляющая – коэффициентом молекулярной диффузии и суммой вторых производных концентраций по соответствующим координатам

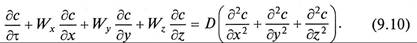
Уравнение (9.10) является дифференциальным уравнением конвективной диффузии.

При массоо6мене в неподвижном слое проекции скорости на оси координат W_x = W_y = =W_z= 0, и уравнение (9.10) преобразуется в дифференциальное уравнение молекулярной диффузии (второй закон Фика)

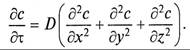
Трудности теоретического описания и расчета процесса массопередачи обусловлены сложностью механизма переноса вещества к границе раздела фаз и от нее, недостаточной изученностью гидродинамических закономерностей турбулентных потоков, особенно вблизи границы раздела фаз.

В связи с этим предложен ряд теоретических моделей, в основу большинства которых положены допущения:

· общее сопротивление процессу массопередачи складывается из сопротивления распределяющих фаз. Сопротивлением поверхности разделав большинстве случаев можно пренебречь;

· на поверхности раздела фазы находятся в равновесии.

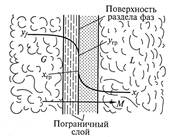
На рис. 9.4 представлена схема массопередачи между система ми жидкость – газ (пар) или жидкость - жидкость. Фазы разделены поверхностью раздела и движутся друг относительно друга с некоторой скоростью.

Процесс массопередачи заключается в переносе распределяемого вещества из фазы G к поверхности раздела фаз (процесс массоотдачи), а затем массоотдачи от поверхности раздела к фазе L.

Процесс массопередачи связан со структурой потока в каждой фазе, которая включает турбулентное ядро потока, где массоперенос осуществляется конвекцией и концентрация компонента практически постоянна. При приближении к поверхности раздела в пограничном слое происходит затухание пульсаций, преобладание механизма молекулярной диффузии, а следовательно, резкое уменьшение концентраций.

Для нахождения скорости перехода вещества из одной фазы к поверхности раздела фаз и далее от нее во вторую фазу используют уравнения массоотдачи, которые для схемы, представленной на рис. 9.4, можно записать как

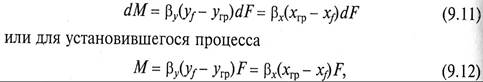
где у_f - у_гр и х_гр - х_f – движущие силы в процессах массоотдачи в фазах G и L; F – поверхность массопередачи; β_y и β_х – коэффициенты массоотдачи (β, м/с, при размерности единичной движу щей силы – кг/м³).

Коэффициент массоотдачи показывает, какое количество вещества переходит из ядра потока к поверхности раздела (или наоборот) через единицу площади поверхности за единицу времени при движущей силе, равной единице, и зависит в первую очередь от гидродинамических условий.

Если равновесная линия массообменного процесса – прямая с тангенсом угла наклона А_равн, то между коэффициентами массопередачи К_y, К_х из уравнений (9.6) (9.7) и коэффициентами массоотдачи β_y, β_х из уравнений (9.11) (9.12) существует однозначная связь

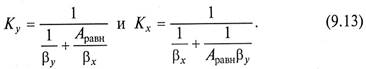
Коэффициент массопередачи показывает, какое количество вещества переходит из одной фазы в другую за единицу времени через единицу площади поверхности контакта фаз при движущей силе массопередачи, равной единице. Размерность коэффициента массопередачи совпадает с размерностью коэффициента массоотдачи.

Поскольку величины, обратные значениям коэффициентов массопередачи, представляют собой общее сопротивление переносу вещества из фазы в фазу (В.3), то выражения в знаменателях уравнений (9.13) представляют сумму сопротивлении массоотдачи в фазах.

Для расчетов коэффициентов массоотдачи β_х и β_y чаще всего используют уравнения, которые получают на основании теории подобия.