Подобие диффузионных процессов

Анализ дифференциальных уравнений, описывающих массообменные процессы с позиций теории подобия, позволил выявить основные критерии подобия процессов массопередачи, приведенные в табл. 9.2.

Некоторые из приведенных критериев носят двойные названия. Первое часто используется в отечественной литературе, второе в зарубежной.

Поскольку гидродинамические характеристики оказывают существенное влияние на процесс массопередачи, они учитываются гидродинамическими критериями Re (вынужденное движение) и Gr (свободное движение).

При подобии процессов переноса массы должно соблюдаться также геометрическое подобие, которое выражается равенством симплексов Г₁, Г₂, ..., Г_n, представляющих собой отношение характерных геометрических размеров объектов системы к некоторому определяющему ее размеру.

Таким образом, критериальная зависимость для описания процесса конвективной массоотдачи с учетом Ре_диф = Pr_диф*Re может быть записана в виде

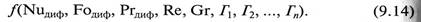
Определяемым критерием в рассматриваемом уравнении является критерий Nu_диф, который нельзя рассчитать используя условия однозначности, так как в него входит определяемый коэффициент массоотдачи β.

Критериальное уравнение (9.14) в этом случае принимает вид

Применительно к конкретным задачам уравнение (9.15) может быть упрощено. Так, при рассмотрении стационарных процессов из него выпадает Fo_диф, вынужденное движение характеризуется только критерием Re и исключает Gr, свободное – наоборот.

Таким образом для установившегося процесса массопередачи при вынужденном движении распределяющей фазы уравнение (9.15) имеет вид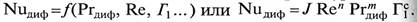

По значениям критериев Nu_{диф y} и Nu_{диф х} определяют величины β_x и β_y

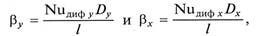
коэффициенты массопередачи К_у и К_х (9.13) и необходимую поверхность контакта фаз (9.7).

Движущая сила процесса массопередачи определяется разностью рабочей и равновесной концентраций и указывает направление осуществления процесса (см. рис. 9.3).

Поскольку движущая сила меняется вдоль поверхности межфазового контакта по высоте аппарата, то при расчетах используют значение средней движущей силы Δу_ср или Δх_ср, входящей в уравнение массопередачи (9.7).

Различают два подхода к расчету средней движущей силы массообменного процесса:

· с линейной равновесной зависимостью;

· с нелинейной равновесной зависимостью.

В случае линейной равновесной зависимости вначале определяется движущая сила в начале и конце процесса как разность соответствующих рабочих и равновесных концентраций. Поскольку одна из них является большей (Δу_max, Δх_max), а другая меньшей (Δу_min, Δх_min), в случае Δу_max/Δу_min ≤ 2 средняя движущая сила определяется как среднеарифметическое

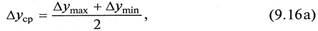
В случае Δу_max/Δу_min > 2 - как среднелогарифмическое

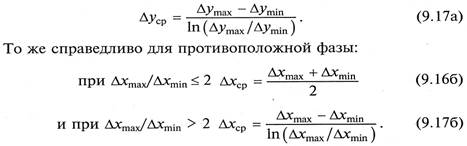
Если равновесная линия является нелинейной, то расчет ведется с использованием чисел единиц переноса, определяющих изменение рабочих концентраций, приходящееся на единицу средней движущей силы,

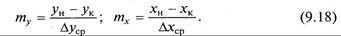
В соответствии с уравнением материального баланса (9.2) -и основного уравнения массопередачи (9.6)

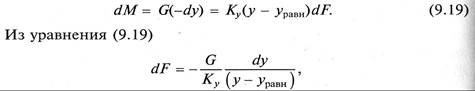
а после интегрирования в пределах 0 – F и у_н – у_к

Сопоставив уравнения (9.7) и (9.20), получим для фазы G среднюю движущую силу при нелинейной равновесной зависимости

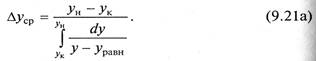
Аналогично для фазы L получим

Поскольку аналитическое вычисление значений Δу_ср и Δх_ср часто невозможно в связи с отсутствием в большинстве случаев математической функции равновесной зависимости, то численные значения интегралов в знаменателях выражений (9.21а,б) определяются графически.

Легко видеть, что численным значением искомого интеграла является площадь под кривой, построенной в соответствующих масштабах в координатах у- 1/(у – у_равн) и ограниченной ординатами у_к и у„ (рис. 9.5). Значение у – у_равн получают в интервале у_н – у_к после построения графиков (см. рис. 9.3).