Понятие о метод проекций

Как отмечалось выше, физическая поверхность Земли представляет собой очень сложную поверхность, и поэтому для изображения ее на картах и планах используют метод проекций в пространстве.

Метод проекций состоит в том, что характерные точки земной поверхности проектируются на поверхность или плоскость относимости. В геодезии используется в основном ортогональные проекции. В таких проекциях линии проектирования должны быть перпендикулярны к поверхности, на которую проектируются точки земной поверхности. Это означает, что проектирование производится по нормали (по перпендикуляру) к поверхности относимости.

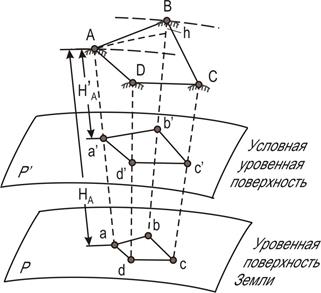
В качестве поверхности относимости в геодезии используется главным образом две поверхности: поверхность референц-эллипсоида (рис. 4.1,а) и горизонтальная плоскость (рис. 4.1,б).

а)	б)
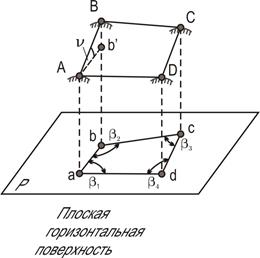
Рис. 4.1 - Метод проекций в геодезии: а – проектирование по нормали к поверхности относимости; б – ортогональное проектирование на горизонтальную поверхность

При высокоточных геодезических работах на значительных по площади территориях за поверхность относимости принимают поверхность референц-эллипсоида.

При выполнении геодезических работ на небольших территориях можно считать, что поверхности эллипсоида и геоида совпадают. Тогда проектирование можно осуществлять на уровневую поверхность по отвесным линиям, а при определенных условиях можно считать, что уровневая поверхность является горизонтальной плоскостью, а отвесные линии параллельны друг другу.

Возникает законный вопрос, на какой площади уровенную поверхность можно считать плоскостью?

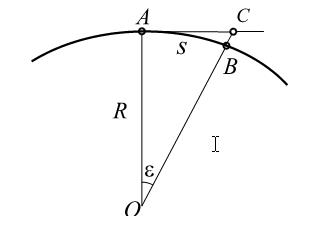
Рис. 4.2 – К решению вопроса об участке, который можно считать плоским

Возьмем линию 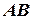на уровенной поверхности Земли, изображаемую сферой радиуса 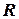(рис. 4.2). Заменим участок сферической уровенной поверхности плоскостью, которая является касательной к сфере в точке 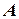. Найдем разницу между длиной дуги 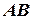, которая равна , и длиной касательной .

Из треугольника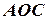

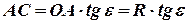
Центральный угол 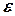(в радианной мере) может быть вычислен по формуле

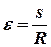
Тогда искомая разница 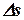будет равна

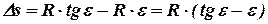
Учитывая, что угол 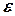небольшой, разложим 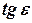в ряд Тейлора, ограничившись двумя членами разложения

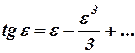
Тогда

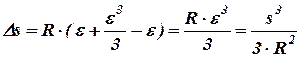(4.1)

С помощью этой формулы нетрудно убедиться в том, что при длине дуги в 10 км величина 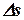меньше 10 см, т.е. принимая уроенную поверхность в пределах радиуса 10 км за плоскость, мы допускаем ошибку меньше 1:1000000 этой дуги, что близко к точности измерений даже при самых высокоточных работах. Следовательно, участок земной поверхности радиусом в 10 км можно принимать за плоскость во всех случаях геодезической практики. При решении некоторых инженерных задач размеры этого участка могут быть расширены приблизительно до радиуса 25-30 км.

Таким образом, проектирование физической поверхности Земли в определенных случаях можно осуществлять на плоскость, считая отвесные линии параллельными одна другой. (рис. 4.1,б).

Пересечение отвесных линий, проходящих через точки 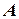, , 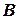, 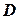земной поверхности, с горизонтальной плоскостью дают точки 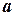, , 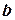, 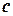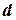. Полученный плоский четырехугольник 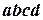представляет собой горизонтальную проекцию пространственного четырехугольника 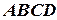. Линии 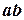, , 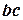, 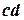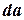называются горизонтальными проложениями линий 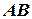, , 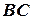, 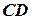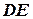местности, а углы между ними 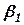, , 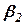, 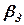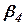- горизонтальными углами.

Таким образом, для изображения фигуры местности на горизонтальной плоскости (в плане) необходимо знать горизонтальные углы между сторонами и горизонтальные проложения сторон.

Для вычисления горизонтальных проложений необходимо знать углы наклона 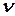(«ню») линий, т.е. углы, образуемые наклонной линией с горизонтальной плоскостью. Тогда, горизонтальное проложение может быть вычислено как

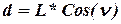, (4.2)

где 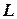- наклонная длина линии.