Поверхность относимости. Эллипсоид вращения. Сфероид. Экватор. Геодезические меридианы и параллели

Одна из главных задач топографии – отображение земной поверхности и объектов, расположенных на ней, на плоскости в виде карт и планов. Но поскольку поверхность геоида, квазигеоида, а тем более физическая поверхность Земли математически неправильные, то с такими поверхностями практически невозможно работать. Поэтому поступают следующим образом.

1. Сначала определяют форму и размеры некоторой модели Земли, поверхность которой является относительно простой, хорошо изученной в геометрическом отношении, удобная для решения на ней геодезических и картографических задач и которая наиболее полным образом характеризует в первом приближении форму и размеры реальной Земли.

2. Затем, приняв поверхность этой модели за отсчетную, определяют относительно нее высоты точек реальной Земли.

Поверхность, которая соответствует принятой модели, называется поверхностью относимости. Т.е. реальная физическая поверхность Земли первоначально отображается на поверхность относимости.

При решении геодезических задач за такую модель Земли принимается эллипсоид вращения (рис. 4).

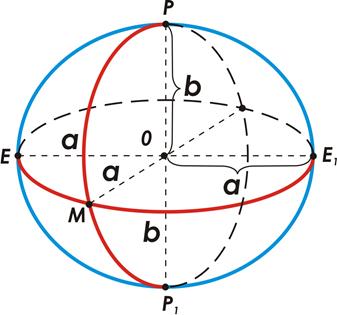
Рис. 2.3 – Эллипсоид вращения - земной эллипсоид

Эта фигура образуется вращением эллипса 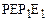вокруг его малой оси 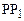, которая совпадает с осью вращения Земли

Размеры эллипсоида характеризуются длинами его полуосей: a - большая полуось, b - малая полуось, и полярным сжатием a:

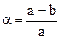(2.1)

Эллипсоид вращения с малым сжатием называется сфероидом.

Линии пересечения поверхности сфероида плоскостями, проходящими через ось вращения 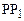, называются геодезическими меридианами и являются эллипсами.

Линии пересечения поверхности сфероида плоскостями, перпендикулярными оси вращения, называются параллелями и являются окружностями.

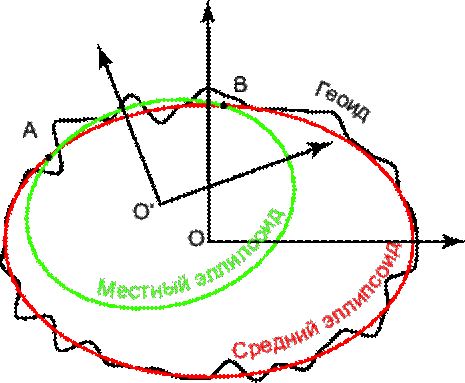
Параметры эллипсоида должны быть такими, чтобы он наилучшим образом подходил к геоиду. В том случае, когда эллипсоид наиболее близок к фигуре Земли в целом, его называют средним или общим земным эллипсоидом (рис. 4).

Рис. 2.4 - Общий земной эллипсоид (средний эллипсоид) и референц-эллипсоид для области AB

В некоторых странах или группе стран во время обработки геодезических измерений используют эллипсоиды с параметрами, полученными по результатам геодезических работ на территории данной страны или нескольких стран. Такие «рабочие» эллипсоиды называются местными эллипсоидами или референц-эллипсоидами (рис. 5). Референц-эллипсоид можно рассматривать как эллипсоид, который наилучшим образом подходит только для некоторой части поверхности Земли.

В Украине, как и в России, а также в бывшем СССР, в качестве отсчетного эллипсоида используется референц-эллипсоид Красовского, который характеризуется следующими параметрами:

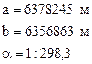
Данный эллипсоид был принят в качестве рабочего в бывшем СССР в 1946 году.

Поскольку полярное сжатие референц-эллипсоида очень маленькое, то при решении многих задач за фигуру Земли принимают сферу, которая равна по объему земному эллипсоиду. Для референц-эллипсоида Красовского радиус такой сферы составляет 6371,11 км.