Детерминированные меры информации.

Для построения метрической функции, определяющей количество информации на основе детерминированной меры,обычно используются алгоритмический [16] илитопологический[20] подходы.

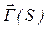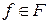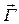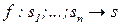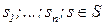При алгоритмическом подходе рассматриваемая система моделируется семантической сетью, представляющей орграф в виде пары (S;F), где S – множество вершин, описывающих предикатную область данной системы, связи (дуги) в которой задаются посредством коммутатора F – набора функций . Пусть в сети (S) имеется алгоритм вывода: , где . Процедура вывода s является упорядоченным множеством B(s) 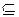U(s), где U(s) – есть объединение всех алгоритмов перехода к вершине s. Пусть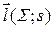 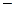множество маршрутов от источников сети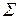 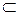S к вершине s в алгоритме вывода B(s). Длина | 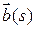| алгоритма B(s) представляет критический путь на B(s) и определяется рекурсивно [10]:

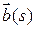| |= max(| 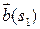|;…;| |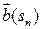)+1. (1.10)

Тогда величина inf | 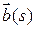| среди всех алгоритмов множества U(s) определяет алгоритмическое количество информации по А.Н. Колмогорову.

Топологический подход к построению метрической функции для определения количества информации формируется с помощью системы покрытий сети 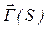, когда параметром оптимизации выступает емкость (мощность) элементов покрытия, что равносильно оптимизации, например, в рамках блочно-модульного обучения [10]. Таким образом, формируется топологическая концепция Н. Рашевского для определения количества информации [20], которая, вообще говоря, не совпадает с алгоритмической концепцией А.Н. Колмогорова [16]. В частности, данная проблематика основательно исследуется в связи с задачами принятия решений при ситуационном управлении сложными системами и, например, в алгоритмах обобщения [21], использующих аппарат покрытий, эффективность принимаемого решения (гипотезы) оценивается с помощью мощностей подмножеств, покрывающих класс элементов обучающей выборки на соответствующей семантической сети.