Стохастические меры информации.
Классический вариант построения метрической функции для определения количества информации на основе стохастической мерывосходит к К. Шеннону [5]. В этом случае количество информации I в сообщении,выражается соотношением
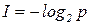 ,(1.5)
,(1.5)
где p – вероятность данного сообщения, а количество информации I измеряется в битах или байтах. Введенное количество информации (1.5), представляет собой типичный пример абстрактной стохастической меры, трактующей информацию, как некоторый груз неопределенности, снятие которой приводит к адекватному восприятию данного сообщения. Реально, однако, почти всегда приходится иметь дело с потоком сообщений с вероятностями 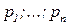 и количество информации, содержащееся в данном потоке сообщений,определяют в виде математического ожидания
и количество информации, содержащееся в данном потоке сообщений,определяют в виде математического ожидания 
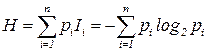 , (1.6)
, (1.6)
где 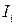 – количество информации, связанное с i-м сообщением. В случае непрерывного потока сообщений в (1.6) следует перейти к интегралу. Величину Н называют информационной энтропией по К. Шеннону [5].
– количество информации, связанное с i-м сообщением. В случае непрерывного потока сообщений в (1.6) следует перейти к интегралу. Величину Н называют информационной энтропией по К. Шеннону [5].
Определения количества информации (1.5); (1.6), представляющие его как меру неопределенности, снятие которой приводит к адекватному управлению процессом, позволяют сформулировать критерий оптимизации управления, известный как принцип минимизации информационной энтропии данного процесса:
 орt H
орt H 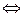 min H (1.7)
min H (1.7)
Фактически, минимизация информационной энтропии в процессе управления означает оптимальную организацию информационных сетей и потоков, реализующих передачу управляющего сигнала в данном процессе. Это приводит к задаче о пропускной способности каналов коммуникаций, которая определяется отношением: 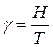 , (1.8)
, (1.8)
где Н – количество информации (энтропия), которую канал связи способен передать за характерное временя Т. К примеру, эксперименты, проведенные Л.Б. Ительсоном [18], позволили оценить пропускную способность учащихся (среднее количество информации, воспринимаемое в единицу времени в процессе обучения), составившую: ~ 6 бит/с – при незнакомых сигналах; ~ 18-20 бит/с – при знакомых, но непривычных сигналах; до 65 бит/с – при хорошо знакомых, привычных сигналах. Данные Ительсона [18] неплохо согласуются с экспериментами по определению минимального времени физиологических реакций, измеряемого при наиболее благоприятных условиях восприятия, которые оценивают пропускную способность центральной нервной системы человека в 30 – 40 бит/с [9]. Сравнивая данные по восприятию с пропускными способностями человеческих органов чувств (для глаза ~ 106-107 бит/с; для уха ~ 103-104 бит/с), можно констатировать, что реально используемые способы передачи информации, как правило, используют незначительную часть пропускной способности существующих линий связи.
Важной количественной характеристикой информации является ее избыточность 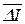 , которая представляет меру возможного увеличения скорости передачи информации за счет использования статистических корреляций между компонентами сообщения, вырабатываемого некоторым источником сообщений. Величину
, которая представляет меру возможного увеличения скорости передачи информации за счет использования статистических корреляций между компонентами сообщения, вырабатываемого некоторым источником сообщений. Величину 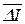 можно определить соотношением:
можно определить соотношением:
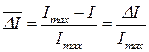 , (1.9)
, (1.9)
где 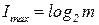
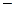 максимальное количество информации, генерируемое дискретным источником в рамках некоторого m-элементного алфавита; I – содержание сообщения, выраженное определенным количеством информации, переданной тем же источником в том же алфавите. Выражение (1.9) описывает случай положительной избыточности (ΔΙ > 0), хотя, при наличии нескольких неоднородных каналов поступления информации, в случае их рассогласования, избыточность информации может иметь отрицательные последствия. Положительная избыточность – это необходимый элемент эстетически значимого произведения искусства [19], а также любого языкового общения [9]. В частности, избыточность письменных сообщений, по данным [9], для литературных текстов в русском языке составляет 76.2%, а для языков романо-германской группы – около 71%. Более высокая избыточность русского языка позволяет точно и красочно передать творческий замысел литературного произведения, тем самым, демонстрируя богатство русского языка, которое так гениально воплощал А.С. Пушкин.
максимальное количество информации, генерируемое дискретным источником в рамках некоторого m-элементного алфавита; I – содержание сообщения, выраженное определенным количеством информации, переданной тем же источником в том же алфавите. Выражение (1.9) описывает случай положительной избыточности (ΔΙ > 0), хотя, при наличии нескольких неоднородных каналов поступления информации, в случае их рассогласования, избыточность информации может иметь отрицательные последствия. Положительная избыточность – это необходимый элемент эстетически значимого произведения искусства [19], а также любого языкового общения [9]. В частности, избыточность письменных сообщений, по данным [9], для литературных текстов в русском языке составляет 76.2%, а для языков романо-германской группы – около 71%. Более высокая избыточность русского языка позволяет точно и красочно передать творческий замысел литературного произведения, тем самым, демонстрируя богатство русского языка, которое так гениально воплощал А.С. Пушкин.
Дата добавления: 2015-08-14; просмотров: 680;
