Формализованное описание кибернетической системы.
С позиций современной алгебры элемент кибернетической системы представляет абстрактный автомат А,который описывается пятеркой (А;S;Z;f;g), где A – множество входных сигналов (входной алфавит), S – множество внутренних состояний; Z – множество выходных сигналов (выходной алфавит); f:S×A→S – функция переходов (в следующее состояние); g:S×A→Z – функция выходов автомата. Формально, автомат – это алгебра с тремя основными множествами А;S;Z и двумя бинарными операциями f и g. Если автомат А находится в состоянии s 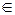 S и получает на входе а
S и получает на входе а 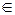 А, то он переходит в состояние f(s;a) и выдает сигнал g(s;a).
А, то он переходит в состояние f(s;a) и выдает сигнал g(s;a).
Автомат А называется конечным, если множества А;S;Z конечны. Это наиболее изученный класс автоматов, к которому, в частности, отнесятся современные компьютеры [14]. Обобщения конечных автоматов происходят по нескольким направлениям: если, например, хотя бы одно из множеств А;S или Z – бесконечное, то соответствующий автомат называют бесконечным; если автоматные функции f;g – есть случайные процессы, то такой автомат называют стохастическим; если А;S или Z представляют собой нечеткие множества [15], то данный автомат называют нечетким и т.д.
Покажем, что алгебраическая структура (А;S;Z;f;g), представляющая автомат А, является универсальным преобразователем информации. Для простоты ограничимся рассмотрением конечных автоматов и заметим, что в реальной ситуации на вход автомата, как правило, подается не одиночный сигнал а 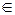 А, а некоторая программа, состоящая из последовательностей элементов (букв) входного алфавита А. Поэтому элементы А резонно рассматривать как систему образующих, порождающих посредством операции конкатенации свободный моноид FA, состоящий из всевозможных последовательностей (слов), построенных из букв алфавита А, включая пустую последовательность е в виде единицы.
А, а некоторая программа, состоящая из последовательностей элементов (букв) входного алфавита А. Поэтому элементы А резонно рассматривать как систему образующих, порождающих посредством операции конкатенации свободный моноид FA, состоящий из всевозможных последовательностей (слов), построенных из букв алфавита А, включая пустую последовательность е в виде единицы.
Пусть автомат А находится в состоянии s 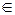 S и на его вход поступает команда в виде последовательности а1а2…аr
S и на его вход поступает команда в виде последовательности а1а2…аr 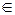 FA, где а1;а2;…;аr
FA, где а1;а2;…;аr 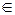 A. Выполнение этой команды предполагает рекурсию
A. Выполнение этой команды предполагает рекурсию
f(s;e)=s
f(s;a1)=f(s;a1)
f(s;a1a2)=f(f(s;a1);а2) (1.1)
. . . . . . . . . . . . . . . . . . . . . . . . . . .
f(s;a1a2…ar)=f(f(s;a1a2…ar-1);аr),
что дает на выходе: g(s;e)=e
g(s;a1)=g(s;a1)
g(s;a1a2)= g(s;a1)g(f(s;a1);а2) (1.2)
. . . . . . . . . . . . . . . . . . . . . . . . . . .
g(s;a1a2…ar)= g(s;a1)g(f(s;a1);a2a3…ar)
Используя (1.1), положим: s1=s
s2= f(s1;a1)
s3= f(s1;a1a2)= f(f(s1;a1);а2)= f(s2;a2) (1.3)
. . . . . . . . . . . . . . . . . . . . . . . . . . .
s4= f(s3;a3);…; sr+1= f(sr;ar)
Из соотношений (1.1), (1.2), (1.3) видно, что, если автомат А находится в состоянии s и на вход поступает команда а1а2…аr 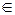 FA, то его состояния последовательно изменяются от s=s1 к s2;s3;..., пока не будет достигнуто состояние sr+1 и выходная последовательность примет вид z1z2z3…zr, где zi=g(si;ai)
FA, то его состояния последовательно изменяются от s=s1 к s2;s3;..., пока не будет достигнуто состояние sr+1 и выходная последовательность примет вид z1z2z3…zr, где zi=g(si;ai) 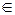 Z, i=
Z, i= 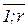 , причем, множество выходных последовательностей, вообще говоря, моноидом быть не обязано.
, причем, множество выходных последовательностей, вообще говоря, моноидом быть не обязано.
Для произвольной последовательности a 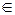 FA введем функцию fa:S
FA введем функцию fa:S 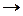 S, так что fa(s)=f(s;a). Тогда
S, так что fa(s)=f(s;a). Тогда 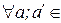 FA: (fa
FA: (fa 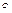
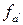 )(s) = fa(
)(s) = fa( 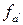 (s))= fa(f (s;
(s))= fa(f (s; 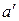 ))= = f(f (s;
))= = f(f (s; 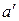 );a)=f (s;
);a)=f (s; 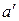 a)=
a)= 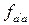 (s)
(s) 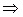 fa
fa 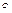
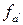 =
= 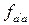 , причем, полагая
, причем, полагая 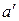 =e, получаем fa
=e, получаем fa 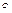
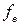 =
= 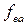 =fa, т.е. функция
=fa, т.е. функция 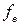 в данном случае выполняет роль единицы. Учитывая, что композиция функций ассоциативна, пара ({fa|a
в данном случае выполняет роль единицы. Учитывая, что композиция функций ассоциативна, пара ({fa|a 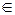 FA};
FA}; 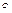 ) является моноидом, который принято называть моноидом автомата А, представляя в виде тройки (А;S;f).
) является моноидом, который принято называть моноидом автомата А, представляя в виде тройки (А;S;f).
Данное обстоятельство представляется важным, поскольку имеет место изоморфизм (А;S;f) 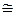 FA. Тогда в свободном моноиде FA, как это следует из теории формальных языков [14], выделяется класс рациональных (или регулярных) языков Rat FA, и всякий такой язык, по теореме С.К. Клини (1956), является распознаваемым. Следовательно, конструкция абстрактного автомата А такова, что входная информация формализуется универсальным алгоритмическим языком, который гарантированно распознается данным автоматом и, тем самым, реализуется соответствующее преобразование поступающей информации.
FA. Тогда в свободном моноиде FA, как это следует из теории формальных языков [14], выделяется класс рациональных (или регулярных) языков Rat FA, и всякий такой язык, по теореме С.К. Клини (1956), является распознаваемым. Следовательно, конструкция абстрактного автомата А такова, что входная информация формализуется универсальным алгоритмическим языком, который гарантированно распознается данным автоматом и, тем самым, реализуется соответствующее преобразование поступающей информации.
Формально кибернетическая системапредставляет некоторый каскад, который формируется из некоторого набора М элементарных абстрактных автоматов путем отождествления выходных сигналов одних автоматов с входными сигналами других. Такие отождествления задаются следующей системой равенств:
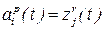 , (1.4)
, (1.4)
где p;r 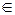 M,
M, 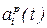
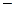 i-я компонента входного сигнала p-го автомата;
i-я компонента входного сигнала p-го автомата; 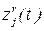
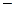 j-я компонента выходного сигнала r-го автомата, причем, равенства (1.4) предусматривают синхронизацию по времени t. При формировании кибернетической системы посредством равенств (1.4) часть компонентов входных сигналов тех или иных автоматов из М может оказаться свободной и в этом случае такие компоненты объединяются, образуя общий входной сигнал описываемой кибернетической системы. Точно также, оставшиеся свободными компоненты выходных сигналов образуют общий выходной сигнал данной кибернетической системы.
j-я компонента выходного сигнала r-го автомата, причем, равенства (1.4) предусматривают синхронизацию по времени t. При формировании кибернетической системы посредством равенств (1.4) часть компонентов входных сигналов тех или иных автоматов из М может оказаться свободной и в этом случае такие компоненты объединяются, образуя общий входной сигнал описываемой кибернетической системы. Точно также, оставшиеся свободными компоненты выходных сигналов образуют общий выходной сигнал данной кибернетической системы.
Элементы кибернетической системы (абстрактные автоматы)могут соединяться параллельно или последовательно. Пусть А1=(А1;S1;Z1;f1;g1); А2=(А2;S2;Z2;f2;g2) – два конечных автомата. Автомат А1 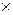 А2=(А1
А2=(А1 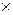 А2; S1
А2; S1 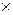 S2; Z1
S2; Z1 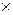 Z2;f; g), где f((s1;s2); (a1;a2))=(f1(s1;a1); f2(s2;a2)); g((s1;s2);(a1;a2))=(g1(s1;a1); g2(s2;a2)) для любых (s1;s2)
Z2;f; g), где f((s1;s2); (a1;a2))=(f1(s1;a1); f2(s2;a2)); g((s1;s2);(a1;a2))=(g1(s1;a1); g2(s2;a2)) для любых (s1;s2) 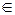 S1
S1 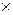 S2; (a1;a2)
S2; (a1;a2) 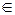 A1
A1  A2, называют параллельным соединением автоматов А1 и А2 (рис. 1.2а). Пусть для автоматов А1 и А2 дополнительно выполняется условие A2=Z1. Тогда последовательное соединение автоматов А1 и А2 представляет автоматА1А2=(A1;S1×S2;Z2;f;g),
A2, называют параллельным соединением автоматов А1 и А2 (рис. 1.2а). Пусть для автоматов А1 и А2 дополнительно выполняется условие A2=Z1. Тогда последовательное соединение автоматов А1 и А2 представляет автоматА1А2=(A1;S1×S2;Z2;f;g),
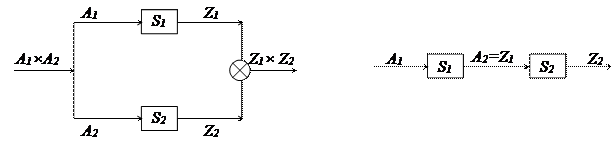 a) б)
a) б)
Рис. 1.2.
где f((s1;s2);a1)=(f1(s1;a1);f2(s2;g1(s1;a1))); g((s1;s2);a1)= g2(s2;g1(s1;a1)) для любых (s1;s2) 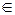 S1
S1 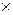 S2; a1
S2; a1 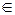 A1 (рис. 1.2б).Таким образом, в рамках абстрактной теории автоматов представлено формализованное описание кибернетической системы, структура которой задается соотношениями (1.4).
A1 (рис. 1.2б).Таким образом, в рамках абстрактной теории автоматов представлено формализованное описание кибернетической системы, структура которой задается соотношениями (1.4).
Дата добавления: 2015-08-14; просмотров: 667;
