Классы задач для кибернетических систем.

Важные классы задач для кибернетических систем представляют задачи их анализа и синтеза. Задача анализа в общем случае формулируется следующим образом: по заданному поведению кибернетической системы определить класс функций (элементов системы), реализующих преобразование информации, отвечающее этому поведению. Задача синтеза кибернетической системы противоположна задаче анализа и подразумевает построение кибернетической системы с наперед заданным поведением, в рамках определенной элементной базы (классов функций), или доказательства факта невозможности реализации заданного поведения при данных условиях.

Другой важный класс задач для кибернетических систем представляют задачи оптимизации, которые могут формулироваться следующим образом. Пусть в рамках соотношений (1.4) задана некоторая кибернетическая система А=(А;S;Z;f;g). Состояния s; 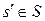системы Аназывают эквивалентными (s~ 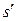), если 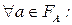g(s;a)= g( 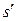;a). Кибернетическая система называется минимальной, если любые два ее различных состояния неэквивалентны.

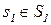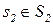Пусть теперь в рамках соотношений (1.4) задаются две кибернетические системы А₁=(А₁;S₁;Z₁;f₁;g₁) и А₂=(А₂;S₂;Z₂;f₂;g₂), которые в принципе могут и совпадать. Состояния и называют эквивалентными (s₁ ~ s₂), если 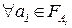, 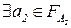: g₁(s₁;a₁) = g₂(s₂;a₂). Если для любого состояния системы А₁ найдется эквивалентное ей состояние системы А₂, то эти системы будем считать эквивалентными (А₁~ А₂) и, таким образом, на множестве кибернетических систем вводится определенное отношение эквивалентности. Задача оптимизации в этом случае может формулироваться на классах эквивалентности, в каждом из которых следует выделить минимальную систему, причем, установлено, что данная задача однозначно разрешима (с точностью до изоморфизма) [14].

Еще один класс задач – это задачи декомпозиции кибернетических систем, когда рассматриваемая система (или ее часть) представляется в виде композиции ее более «мелких» элементов (подсистем). Фундаментальным результатом в теории декомпозиции автоматов является теорема Крона-Роудза [14], устанавливающая все классы неприводимых автоматов, из которых любая конечная кибернетическая система может быть «собрана» посредством последовательных и параллельных соединений. Однако в приложениях особенно важным является случай, когда декомпозиция кибернетической системы сводится к комбинации двух ее подсистем – управляющей и управляемой, которые связаны каналом обратной связи, так, как показано на рис. 1.3, где управляющая подсистема D путем управляющего сигнала x и обратной связи y проводит управление (x;y) управляемой подсистемой U, испытывающей внешнее воздействие u, причем, результаты управления контролируются критерием качества v.

Рис. 1.3.

Задача синтеза в этом случае обычно ставится следующим образом: для данной системы U, при заданном внешнем воздействии u и заданном критерии качества управления v определить управляющую систему D, которая посредством управления (x;y), обеспечивает требуемое поведение критерия качества v.

Представленные классы задач управления, имеют довольно широкие приложения, включая управление когнитивными процессами в процессе обучения и менеджмент.