Спектральная плотность стационарного случайного процесса.

Введём функцию 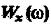- спектральной плотности мощности процесса 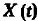(спектр мощности).

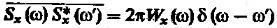(6).

Подставив (6) в (4) получаем:

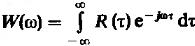(7). Или (8).

Формула (7) и (8) составляют содержание теоремы Винера – Хинчина. Если 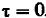и поскольку 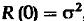, получаем:

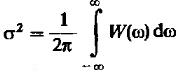(9)

Дисперсия 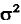равная средней мощности функций спектрального случайного процесса, есть сумма вкладов от всех участков частотной оси.

Односторонний спектр мощности .

Т.к 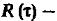чётная функция 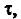соответствующий спектральной мощности 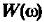четная функция частоты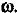

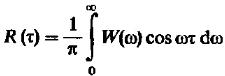(10)

(11)

Введём односторонний спектр мощности:

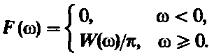(12)

Функция 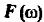позволяет вычислить дисперсию стационарного случайного процесса, причём интегрированная по положительным частотам :

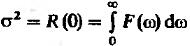(13).

В технических расчётах вводят односторонний спектр мощности N (f ) – представляющий собой среднюю мощность случайного процесса, приходящегося на интервал частот шириной в 1кГц.

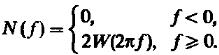при этом легко видеть:

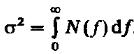(14)

3.Интервал корреляции.

Случайные процессы в радиотехнике обладают следующими свойствами: их функция корреляции стремится к нулю, с увеличением временного сдвига 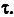числовой характеристикой для скорости изменения реализации случайного процесса является интервал корреляции .

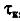(15)

Эффективная ширина спектра.

Рассмотрим выражение:

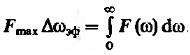(16)

Где 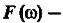односторонний спектр мощности,

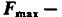экстремальное значение этой функции на интервале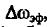

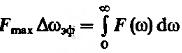(17)

Этой величиной часто пользуются для инженерного расчёта дисперсии шумового сигнала.

4.Белый шум.

В радиотехнике так называется стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности:

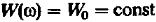(18)

Термин «белый шум» подчёркивает аналогию с «белым» (естественным) светом у которого в пределах видимого диапазона интенсивность всех спектральных составляющих одинакова. По теореме Винера – Хинчина:

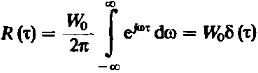(19).

Средняя мощность (дисперсия) белого шума неограниченно велика.