Синфазные и квадратурные составляющие.
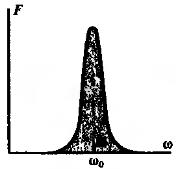
В радиотехнических задачах важную роль играет особый класс случайных процессов, спектральная плотность мощности которых имеет частоты 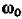 , отличают от нуля. Функция корреляции узкополосного случайного процесса по теореме Винера – Хинчина
, отличают от нуля. Функция корреляции узкополосного случайного процесса по теореме Винера – Хинчина
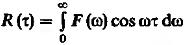 (1) заменим переменную
(1) заменим переменную 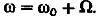 , тогда
, тогда 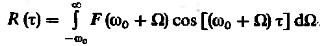 (2) заменим -
(2) заменим - 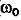 на
на 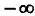 тогда:
тогда:
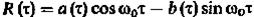 (3)
(3)
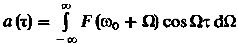 (4) – чётная функция
(4) – чётная функция
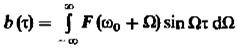 – нечётная функция.
– нечётная функция.
Удобно ввести нормированную огибающую S ( 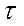 ) функции корреляции узкополосного случайного процесса определив её
) функции корреляции узкополосного случайного процесса определив её 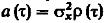 тогда
тогда 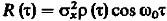 (5)
(5)
Из 5 следует, что отдельные реализации узкополосного случайного процесса могут представлять квазигармонические колебания:
 (6)
(6)
У которой огибающая U(t) и начальная фаза 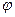 (t). Представим 6 как сумму синфазной и квадратурной составляющей:
(t). Представим 6 как сумму синфазной и квадратурной составляющей:
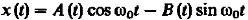 (7)
(7)
Введём случайный процесс Y(t), сопряжённой с исходными процессами X(  ). Его реализацией являются преобразования Гильберта.
). Его реализацией являются преобразования Гильберта.
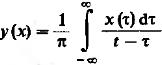 (8)
(8)
Из 7 и 8 можно получить:
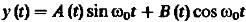 (9)
(9)
От туда для мгновенных значений огибающей 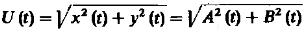 (10) и начальной фазы:
(10) и начальной фазы:
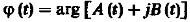 (11)
(11)
Статические свойства сопряженного процесса.
Если  то и
то и 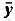 так же равно нулю, пусть X(t) гауссов процесс, а преобразование Гильберта, то Y(t) – тоже гауссов процесс. Если
так же равно нулю, пусть X(t) гауссов процесс, а преобразование Гильберта, то Y(t) – тоже гауссов процесс. Если 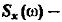 спектральная плотность реализации x(t), то
спектральная плотность реализации x(t), то  (12).
(12).
Модули спектральной плотности совпадают т.е. 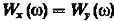 отсюда:
отсюда:
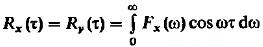 (13) и процесс Y(t) – стационарен. Функцию взаимной корреляции можно определить:
(13) и процесс Y(t) – стационарен. Функцию взаимной корреляции можно определить:
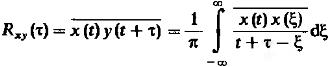
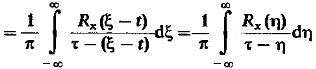 (14) – это нечто иное как преобразование Гильберта от X(t).
(14) – это нечто иное как преобразование Гильберта от X(t).
 (15)
(15)
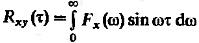 (16)
(16)
2.Корреляцтонные свойства синфазной и квадратурной амплитуд.
Пусть A(t) и B(t) – выражаются следующим образом:
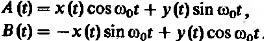 (17)
(17)
Определим корреляцию процесса A.
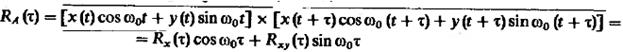 (18).
(18).
С учётом 2 и 16, 18 можно выразить 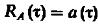 (19).
(19).
Аналогично 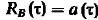 (20) и
(20) и 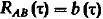 (21). Если
(21). Если 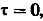 то
то 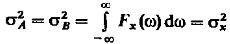 (22).
(22).
Дата добавления: 2015-08-14; просмотров: 1688;
