Спектральные плотности реализации.

Рассмотрим стационарный случайный процесс X(t), с первым математическим ожиданием 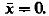Саму функцию модно найти с помощью обратного преобразования Фурье:

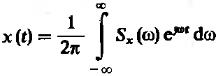(1)

Свойства случайной спектральной.

Усредним значения сигналов по ансамблю реализации:

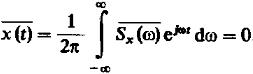(2)

Т.к. сигнал вещественный, то

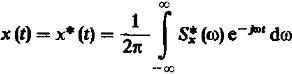(3)

И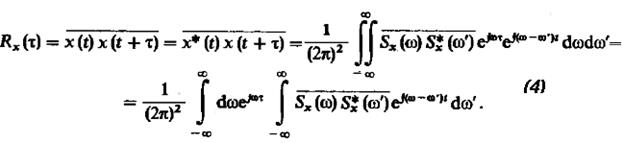

Во внутреннем подынтегральном выражении содержится множитель 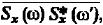, который имеет смысл функции корреляции случайной спектральной плотности, чтобы 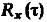не зависело отt необходимо: 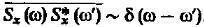(5) такой вид корреляционной связи называется – дельта- коррелированностью.