Определение координат местоположения ЛА
Для решения навигационных задач принимается модель движения центра масс ЛА в прямоугольной системе координат:
 , ,
| (5) |
где 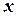 ,
, 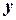 - координаты местоположения ЛА;
- координаты местоположения ЛА;
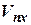 ,
, 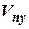 - скорость смены координат в направлении осей
- скорость смены координат в направлении осей  и
и 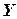 .
.
Таким образом, текущие координаты местоположения ЛА могут быть получены путем интегрирования (5) при условии  и
и 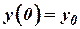 :
:
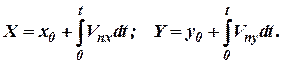
| (6) |
В том случае, если за навигационную систему координат используется правая ортодромическая система координат, единая для всего района полетов, то уравнение (6) будет иметь вид:
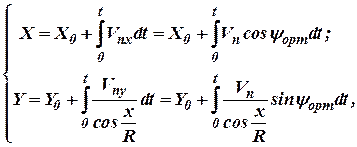
| (7) |
где 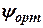 - ортодромический курс ЛА;
- ортодромический курс ЛА;
 - радиус Земли.
- радиус Земли.
Реализация модели (5) осуществляется в ПНК при помощи ВЧУ (аналогового или цифрового). В остальных случаях решаются такие уравнения:
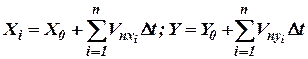
|
или (8)
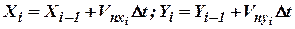 , ,
|
где 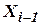 и
и 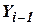 - координаты местоположения ЛА на
- координаты местоположения ЛА на 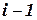 шаге вычислений;
шаге вычислений;
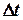 - длительность цикла вычислений
- длительность цикла вычислений  и зависит от условий полета и типа БЦВМ.
и зависит от условий полета и типа БЦВМ.
В случае использования для счисления пути геоцентрической системы координат математическая модель движения ЛА, используемая в БЦВМ, имеет вид
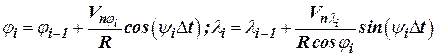 , ,
|
где  - истинный курс ЛА.
- истинный курс ЛА.
В современных навигационных комплексах используют следующие режимы счисления пути:
· инерциальный;
· инерциально-доплеровский;
· курсо-воздушный.
Основным режимом является инерциальный или инерциально-доплеровский. Курсо-воздушный режим (курс – от КС или ИНС, воздушная скорость – от СВС) рассматривается как резервный.
Уравнения оценки ошибки в определении координаты Х местоположения ЛА инерциальным способом имеет вид:
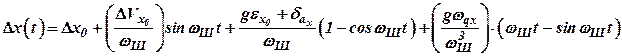 , ,
|
где 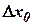 - начальная ошибка выставки ИНС по координате Х;
- начальная ошибка выставки ИНС по координате Х;
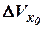 - начальная ошибка выставки ИНС по скорости;
- начальная ошибка выставки ИНС по скорости;
 - начальная ошибка выставки гироплатформы ИНС;
- начальная ошибка выставки гироплатформы ИНС;
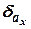 - ошибка измерения ускорения ЛА акселерометра;
- ошибка измерения ускорения ЛА акселерометра;
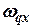 - угловая скорость дрейфа гироплатформы;
- угловая скорость дрейфа гироплатформы;
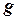 - ускорение свободного падения;
- ускорение свободного падения;
 - частота Шулера.
- частота Шулера.
Аналогичное уравнение оценки ошибки определения координаты У. Таким образом, в общем случае ошибка в определении координат местоположения ЛА с помощью ИНС состоит из 4-х составляющих:
· 1-я – постоянной;
· 2-я – колебательная с периодом Шулера;
· 3-я – колебательная с периодом Шулера;
· 4-я – увеличивающаяся со временем и моделируемая колебаниями с периодом Шулера.
Если преимущества ИНС очевидны – высокая помехозащищенность, автономность, то система ИНС-ДИСС имеет некоторые недостатки.
Современные ДИСС обеспечивают высокую точность измерения проекции скорости полета в направлении излучения 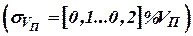 . Но сохранение такой точности задача чрезвычайно сложная из-за пересчета измеренных составляющих путевой скорости по оси системы координат счисления пути. Рассмотрим схему алгоритма такого пересчета.
. Но сохранение такой точности задача чрезвычайно сложная из-за пересчета измеренных составляющих путевой скорости по оси системы координат счисления пути. Рассмотрим схему алгоритма такого пересчета.
ДИСС имеет 3 или 4 измерительных луча, ориентированных под фиксированными углами 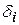 относительно плоскости антенной системы. Доплеровские частоты
относительно плоскости антенной системы. Доплеровские частоты 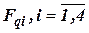 совместно с информацией о характере отражающей поверхности (поправка
совместно с информацией о характере отражающей поверхности (поправка 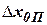 ) является выходными сигналами ДИСС, согласно которым в БЦВМ осуществляется вычисление составляющих скорости ЛА в проекциях на оси системы координат, связанной с антенной системою ДИСС, то есть
) является выходными сигналами ДИСС, согласно которым в БЦВМ осуществляется вычисление составляющих скорости ЛА в проекциях на оси системы координат, связанной с антенной системою ДИСС, то есть 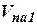 ,
, 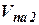 ,
, 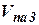 (рис. 5).
(рис. 5).
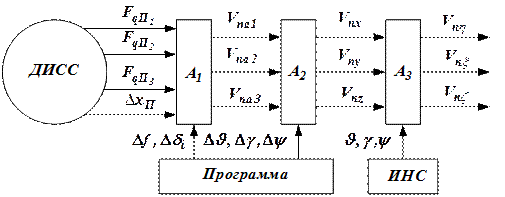
Рисунок 5 Система пересчета составляющих скоростей с ДИСС
в составляющие систему координат ИНС
Здесь: 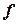 - частота передатчика;
- частота передатчика;
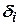 -углы установки лучей;
-углы установки лучей;
 - алгоритм учета погрешностей ДИСС;
- алгоритм учета погрешностей ДИСС;
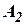 - алгоритмы пересчета составляющих путевой скорости на оси, связанные с корпусом гироплатформы ИНС;
- алгоритмы пересчета составляющих путевой скорости на оси, связанные с корпусом гироплатформы ИНС;
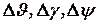 - ошибки взаимной ориентации ДИСС и ИНС;
- ошибки взаимной ориентации ДИСС и ИНС;
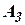 - алгоритм пересчета скоростей от связанной системой координат с корпусом гироплатформы в составляющие путевой скорости, например, относительно инерциальной или стартовой системы координат;
- алгоритм пересчета скоростей от связанной системой координат с корпусом гироплатформы в составляющие путевой скорости, например, относительно инерциальной или стартовой системы координат;
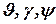 - углы, измеряемые ИНС.
- углы, измеряемые ИНС.
Современные ДИСС измеряют путевую скорость в диапазоне 150…2500 км/час, угол сноса 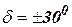 и на высотах 15…20000 м. Заметим, что при маневрировании, наборах высоты, крена и тангажа
и на высотах 15…20000 м. Заметим, что при маневрировании, наборах высоты, крена и тангажа 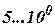 точности измерении
точности измерении 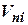 и
и  низкие.
низкие.
Как упоминалось, резервной системой является курсо-воздушная система счисления координат местоположения ЛА.
Составляющие путевой скорости ЛА 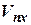 и
и 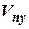 в случае воздушного счисления и правой ортодромической системы координат (рис. 6) могут быть определены так:
в случае воздушного счисления и правой ортодромической системы координат (рис. 6) могут быть определены так:
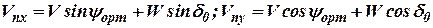
|
где 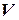 - воздушная скорость ЛА (измеряется системой СВС);
- воздушная скорость ЛА (измеряется системой СВС);
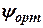 - ортодромический курс ЛА (измеряется курсовой системой);
- ортодромический курс ЛА (измеряется курсовой системой);
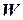 - скорость ветра;
- скорость ветра;
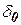 ортодромическое направление ветра.
ортодромическое направление ветра.
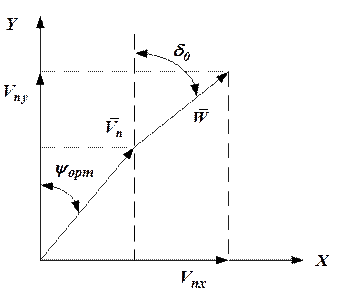
Рисунок 6
Характерные значения точности счисления пути для различных режимов работы ПНК, которые, как правило, приводятся в виде линейных зависимостей среднеквадратичного отклонения (СКО) круговой ошибки от пройденного пути 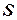 или времени полета
или времени полета 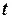 , то есть
, то есть 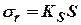 или
или 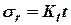 приведены в табл.1.
приведены в табл.1.
Таблица 1
| Режимы счисления | Ошибка (СКО) | |
| Курсо-воздушный | 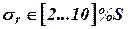
| |
| Инерциально-доплеровский | 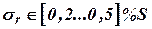
| |
| Инерциальные | Грубые ИНС | 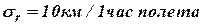
|
| Средний класс ИНС | 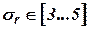 
| |
| Прецизионные ИНС | 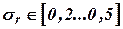 
|
Дата добавления: 2015-08-14; просмотров: 1613;
