Пример. Рассмотрим систему измерения углового положения ЛА с использованием МНК
Рассмотрим систему измерения углового положения ЛА с использованием МНК. В данной системе на основе информации от трех идентичных ИНС вычисляется угол крена ЛА. Показания первой, второй и третей ИНС соответственно равны:

| (1) |
где  - текущее значение угла крена;
- текущее значение угла крена;
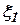 ,
, 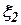 ,
,  - ошибки ИНС (компоненты вектора
- ошибки ИНС (компоненты вектора 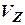 ).
).
В матричной форме (1) имеет вид
 , ,
| (2) |
где  ;
; 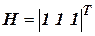 ;
;  ;
; 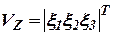 .
.
Итак, необходимо в соответствии с наблюдением 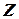 и заданною матрицею наблюдения
и заданною матрицею наблюдения  осуществить оценку состояния вектора
осуществить оценку состояния вектора  .
.
Оценкой угла крена согласно МНК является:
 , ,
| (3) |
где а) 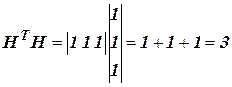 ;
;
б) 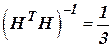 ;
;
в) 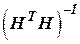
 =
= 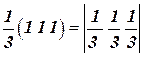 .
.
Полученные значения подставим в (3):
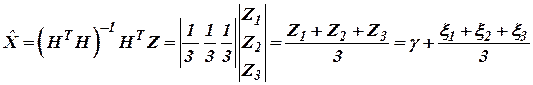 . .
|
Таким образом, в данном случае значение крена определяется как среднее арифметическое показаний трех инерциальных систем.
Алгоритм оценки согласно метода максимума правдоподобия (ММП)
Алгоритм оценки согласно ММП как и алгоритм оценки согласно МНК требует накопления измерений, то есть наличия вектора наблюдения. При этом предполагается, что ошибки измерений распределены согласно нормальному закону. Тогда плотность распределения вероятности вектора 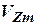 (возмущения) имеет вид:
(возмущения) имеет вид:
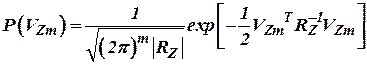 , ,
| (12) |
где 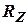 - корреляционная матрица ошибок измерения;
- корреляционная матрица ошибок измерения;
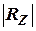 - определитель матрицы
- определитель матрицы 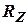 .
.
Использование алгоритма ММП предусматривает наличие не особой матрицы 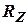 , то есть
, то есть  .
.
Так как  , то отсюда
, то отсюда
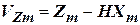
| (13) |
и после подстановки (13) в (12), получим функцию правдоподобия  :
:
 , ,
| (14) |
где  - функция правдоподобия.
- функция правдоподобия.
Функция  представляет собой плотность распределения ошибок измерения.
представляет собой плотность распределения ошибок измерения.
Необходимо выбрать такую оценку 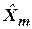 , при которой функция правдоподобия
, при которой функция правдоподобия  преобразуется в максимум, который соответствует минимуму квадратов отклонений измеряемых координат вектора
преобразуется в максимум, который соответствует минимуму квадратов отклонений измеряемых координат вектора 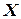 от их действительного значения, для чего необходимо, чтобы
от их действительного значения, для чего необходимо, чтобы
 . .
|
На практике более рационально вычисление не самой функции правдоподобия, а ее логарифма, то есть:
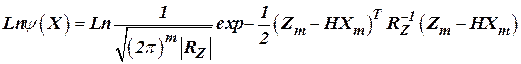 . .
| (15) |
Найдя производную уравнения (15) по компонентам вектора 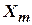 и приравнивая полученный результат нулю, получим
и приравнивая полученный результат нулю, получим

| (16) |
Как видно из (16) одно слагаемое есть транспонированным выражением другого, поэтому достаточно приравнять нулю, например первое слагаемое:
 =0, =0,
|
откуда
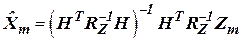 . .
| (17) |
Выражение (17) является исходным для разработки алгоритма оптимальной оценки вектора состояния системы измерений согласно метода максимума правдоподобия. Таким образом, для определения данных оценок, прежде всего необходимо:
· осуществить накопления наблюдений 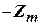 ;
;
· определить корреляционную матрицу 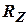 ошибок измерений;
ошибок измерений;
· определить матрицу связи наблюдения  .
.
Структурная схема получения оптимальных оценок согласно метода ММП показана на рис. 2.

Рисунок 2
Как и для алгоритма по МНК при получении оценки вектора состояния, 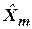 так и согласно ММП необходимо осуществлять накопление результатов измерений
так и согласно ММП необходимо осуществлять накопление результатов измерений 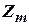 . В связи с этим и в этом случае метод ММП пригоден при условии измерения одного и того же параметра несколькими системами в одни и те же моменты времени.
. В связи с этим и в этом случае метод ММП пригоден при условии измерения одного и того же параметра несколькими системами в одни и те же моменты времени.
Пример.
Географическая широта ЛА  измеряется с помощью ИНС и астроориентатора (звездно-солнечного) ЗСО, ошибки ИНС и ЗСО некоррелированы. Согласно паспортным данным дисперсии ошибок ИНС и ЗСО составляют:
измеряется с помощью ИНС и астроориентатора (звездно-солнечного) ЗСО, ошибки ИНС и ЗСО некоррелированы. Согласно паспортным данным дисперсии ошибок ИНС и ЗСО составляют:
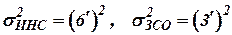 .
.
Требуется осуществить оценку определения широты  используя метод максимального правдоподобия при условии, что показания ИНС на данный момент времени составляют
используя метод максимального правдоподобия при условии, что показания ИНС на данный момент времени составляют 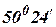 , а показания ЗСО соответственно
, а показания ЗСО соответственно 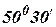 .
.
Решение.Оценка параметра 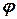 методом ММП может быть может быть осуществлена в соответствии с выражением (17),
методом ММП может быть может быть осуществлена в соответствии с выражением (17),
где 
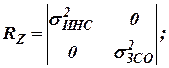

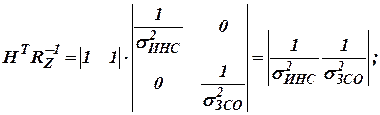
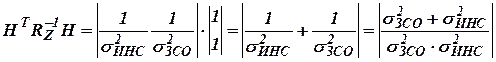 ;
;
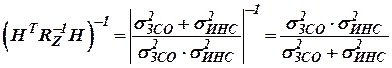 ;
;
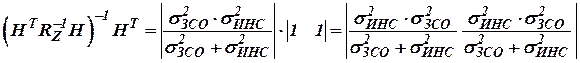 ;
;

Таким образом, оценка координат  по результатам измерений ИНС и ЗСО
по результатам измерений ИНС и ЗСО
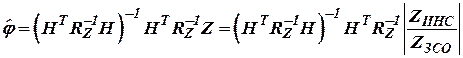 .
.
После подстановки численных значений имеем:
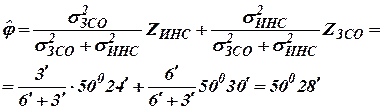 .
.
Дата добавления: 2015-08-14; просмотров: 1176;
