Например.
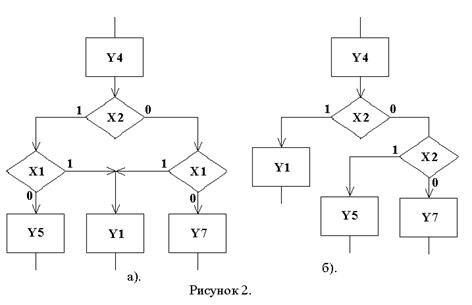
Дан фрагмент ГСА (рис.2а). Запишем формулу перехода Y4®U b4sּYs:
Y4 ® X2 ØX1 Y5 Ú X2 X1 Y1 Ú ØX2 X1 Y1 Ú ØX2 ØX1 Y7.
Данному фрагменту ГСА соответствует следующее разложение формулы перехода по переменным X1 и X2. Разложим исходную формулу по переменной X2:
Y4®X2(X1Y1ÚØX1Y5)ÚØX2(X1Y1ÚØX1Y7).
Разложим исходную формулу по переменной X1:
Y4®X1(X2Y1ÚØX2Y1)ÚØX1(X2Y5ÚØX2Y7)®
® X1Y1ØX1(X2Y5ÚØX2Y7).
Этому разложению соответствует фрагмент ГСА, приведенный на рис.2б.
Объединение ГСА с помощью МСА
В объединяемых ГСА должны встречаться одинаковые операторные и условные вершины (одинаково обозначенные и имеющие одинаковый смысл: в одинаково обозначенных вершинах должны быть одинаковые буквы алфавитов W и Z).
Для объединяемых ГСА строятся МСА, затем строится и заполняется объединённая МСА, записываются формулы переходов и после их разложения по переменным Xsj строятся фрагменты объединённой ГСА, которые затем объединяются путем совмещения операторных вершин. При записи объединённой МСА вводятся дополнительные логические условия (вершины), обеспечивающие заданный алгоритм работы автомата.
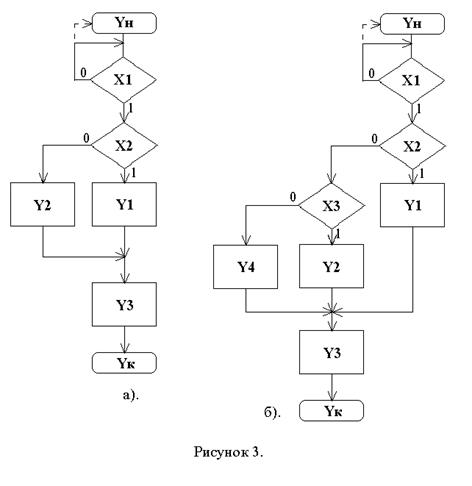
Например, даны две ГСА: Г1 (рис.3а) и Г2 (рис.3б). В этих ГСА встречаются одинаковые операторные и условные вершины. Составим для Г1 матрицу МСА1, а для Г2 матрицу МСА2.
Так как объединяются всего две ГСА, то введём одну дополнительную переменную (логическое условие) P. Условие Р будет определять, по какому пути будут идти переходы в объединенной ГСА в зависимости от того, какой алгоритм реализуется в настоящий момент.
Пусть для Г1 условие P = 1, а для Г2 - P = 0.
МСА1
| Ym\ Ys | Yн | Y1 | Y2 | Y3 | Yк |
| Yн | ØX1 | X1X2 | X1ØX2 | - | - |
| Y1 | |||||
| Y2 | |||||
| Y3 |
Построим объединённую МСА используя условие Р, если выполняется алгоритм по ГСА Г1 и условие ØP, если выполняется алгоритм по ГСА Г2 .
МСА2
| Ym\ Ys | Yн | Y1 | Y2 | Y3 | Y4 | Yк |
| Yн | ØX1 | X1X2 | X1ØX2X3 | - | X1ØX2ØX3 | |
| Y1 | ||||||
| Y2 | ||||||
| Y3 | ||||||
| Y4 |
МСА -объединенная
| Ym\Ys | Yн | Y1 | Y2 | Y3 | Y4 | Yк |
| Yн | PØX1 ØPØX1 | PX1X2 ØP X1X2 | PX1ØX2 ØP X1ØX2X3 | - | ØPX1ØX2ØX3 | - |
| Y1 | P ØP | |||||
| Y2 | P ØP | |||||
| Y3 | P ØP | |||||
| Y4 | ØP |
Запишем формулы переходов по объединенной МСА:
Y1® (PÚØP)Y3 ®Y3
Y2® (PÚØP)Y3 ®Y3
Y3® (PÚØP)Yk ®Yk
Y4® ØPY3 ®Y3, т. к. в строке Y4 нет P, а значит в Г1 нет вершины Y4 , и условие ØР из формулы можно исключить.
Yн® (PÚØP)ØX1Yн Ú (PÚØP)X1X2Y1 Ú PX1ØX2Y2 ÚØ PX1ØX2X3Y2 Ú
Ú ØPX1ØX2ØX3Y4 ®
® ØX1Yн Ú X1X2Y1 Ú PX1ØX2Y2 Ú ØPX1ØX2X3Y2 Ú ØPX1ØX2ØX3Y4
Формулы Y1 – Y4 – простые, их не надо разлагать. Разложение Yн удобно начинать с переменной, чаще всего встречающейся в формуле. Это переменная X1 :
Yн ® ØX1(Yн) Ú X1(X2Y1 Ú PØX2Y2 Ú Ø PØX2X3Y2Ú ØPØX2ØX3Y4);
Далее разложим формулу по X2 :
Yн ® ØX1(Yн) Ú X1(X2(Y1) Ú ØX2(PY2 ÚØ PX3Y2 Ú ØPØX3Y4));
Далее разложим формулу по X3. Так как в последнем разложении в выражении PY2 не содержится переменной X3, преобразуем его следующим образом: PY2 = PY2 (X3ÚØX3) и получим:
Yн ® ØX1(Yн) Ú X1(X2(Y1) Ú ØX2(X3(PY2ÚØPY2) ÚØX3(PY2 Ú ØPY4))) ® ®ØX1(Yн) Ú X1(X2(Y1) Ú ØX2(X3(Y2) ÚØX3(PY2 Ú ØPY4)))..
По полученным объединенным формулам переходов построим фрагменты объединенной ГСА (Рис.4а):
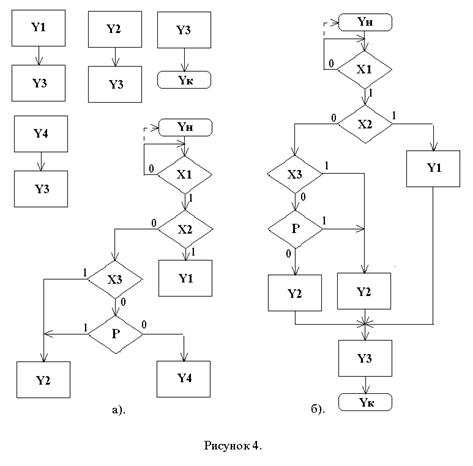
Объединим фрагменты ГСА, учитывая, что не может быть двух операторных вершин одного вида (Рис. 4б). Вид объединённой ГСА зависит от вида фрагментов (подграфов), которые, в свою очередь, зависят от порядка разложения формул перехода.
Дата добавления: 2015-08-11; просмотров: 1269;
