ФИЛЬТРА КАЛМАНА
Алгоритм непрерывного оптимального фильтра Калмана (ОФК) объединяет решение двух задач: наблюдения и фильтрации. Принцип построения ОФК рассмотрим для случая линейной системы, описываемой уравнениями:
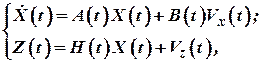
| (4) |
где
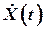 - n-мерный вектор состояния системы;
- n-мерный вектор состояния системы;
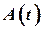 - квадратичная матрица коэффициентов системы размеренности n n;
- квадратичная матрица коэффициентов системы размеренности n n;
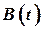 - матрица возмущений;
- матрица возмущений;
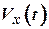 - k-мерный вектор возмущения;
- k-мерный вектор возмущения;
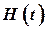 - матрица связи ( матрица наблюдений);
- матрица связи ( матрица наблюдений);
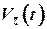 - вектор ошибок измерений m n.
- вектор ошибок измерений m n.
При этом ставится задача: найти такие оценки 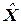 , чтобы ошибка оценки были минимальными, что соответствует необходимости обеспечения минимума суммы диагональных элементов матрицы
, чтобы ошибка оценки были минимальными, что соответствует необходимости обеспечения минимума суммы диагональных элементов матрицы
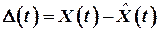
| (5) | |
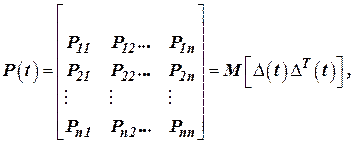
| (6) | |
где 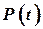 - так называемая квадратичная матрица;
- так называемая квадратичная матрица;
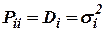 - диагональные элементы матрицы характеризуют дисперсии ошибок оценки совпадающих координат
- диагональные элементы матрицы характеризуют дисперсии ошибок оценки совпадающих координат 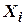 ;
;
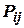 - элементы матрицы, характеризующие взаимную корреляцию фазовых координат
- элементы матрицы, характеризующие взаимную корреляцию фазовых координат 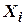 .
.
Известно, что для динамической системы (4) оптимальным фильтром, который обеспечивает минимум следа матрицы 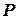 обеспечивает алгоритм, состоящий из 3-х блоков:
обеспечивает алгоритм, состоящий из 3-х блоков:
1. Основного блока
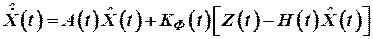 ; ;
| (7) |
2. Блока вычисления коэффициентов коррекции
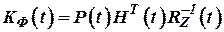 ; ;
| (8) |
3. Блока решения уравнения ковариации
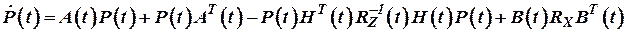 . .
| (9) |
Данный алгоритм обеспечивает оценку всех координат вектора 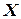 при выполнении условий наблюдаемости динамической системы. Особенности данного алгоритма заключаются в выборе коэффициентов матрицы
при выполнении условий наблюдаемости динамической системы. Особенности данного алгоритма заключаются в выборе коэффициентов матрицы 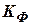 . Выходные значения оценки
. Выходные значения оценки 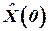 определяются на основании предварительной информации о координатах вектора
определяются на основании предварительной информации о координатах вектора 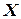 . Ковариационную матрицу текущих ошибок оценки
. Ковариационную матрицу текущих ошибок оценки 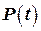 необходимо вычислять постоянно в процессе оценивания или предварительно (априорно), если есть такая возможность.
необходимо вычислять постоянно в процессе оценивания или предварительно (априорно), если есть такая возможность.
Содержание уравнения ковариации, согласно которому вычисляется матрица 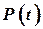 , поясняется так:
, поясняется так:
· если модель динамической системы идеально точно, то реальные ошибки оценки для фильтра, построенного в соответствии с этим уравнением, будут совпадать с ковариациями 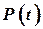 и при этом они будут минимальными. Таким образом, оптимальность фильтра будет достигнута только в случае точного описания структуры модели системы и правильно выбранных параметров:
и при этом они будут минимальными. Таким образом, оптимальность фильтра будет достигнута только в случае точного описания структуры модели системы и правильно выбранных параметров: 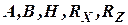 .
.
Вот почему во время синтеза системы оценивания особенное внимание уделяют процессу разработки математических моделей измерителей и исследуемой системы.
Рассмотрим физический смысл отдельных элементов ОФК.
а) В уравнении ковариации (9) член 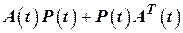 характеризует смену ошибки в результате собственного движения системы. Для устойчивой системы элементы матрицы
характеризует смену ошибки в результате собственного движения системы. Для устойчивой системы элементы матрицы 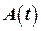 (
( 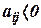 ), что означает уменьшение скорости смены дисперсий ошибок оценки совпадающих координат (
), что означает уменьшение скорости смены дисперсий ошибок оценки совпадающих координат (  ) и приводит к уменьшению ошибок, поскольку
) и приводит к уменьшению ошибок, поскольку 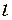 устойчивой системе и
устойчивой системе и 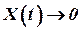 и
и 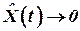 , то есть начальная неопределенность со временем уменьшается.
, то есть начальная неопределенность со временем уменьшается.
б) Множитель 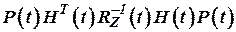 характеризует эффект коррекции оценок от измерителей и всегда определяет
характеризует эффект коррекции оценок от измерителей и всегда определяет 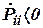 , то есть указывает на уменьшение ошибок оценивания.
, то есть указывает на уменьшение ошибок оценивания.
в) Множитель 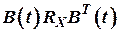 характеризует величину неопределенности контролируемого процесса и всегда выражает, что
характеризует величину неопределенности контролируемого процесса и всегда выражает, что 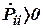 , а следовательно, ошибки оценивания не могут быть полностью сведены до нуля.
, а следовательно, ошибки оценивания не могут быть полностью сведены до нуля.
Заметим, что поскольку уравнение ковариаций (9) автономно и не связано с реальными измерениями 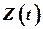 , то его решение может быть выполнено отдельно от основного алгоритма фильтра и даже задолго. Перед решением уравнения ковариаций необходимо оценить и задать начальное значение
, то его решение может быть выполнено отдельно от основного алгоритма фильтра и даже задолго. Перед решением уравнения ковариаций необходимо оценить и задать начальное значение 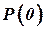 на основе анализа точности информации о координатах вектора
на основе анализа точности информации о координатах вектора 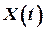 и начальные значения оценки
и начальные значения оценки 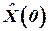 , которая существует до включения фильтра. На практике обычно ограничиваются заданием главной диагонали
, которая существует до включения фильтра. На практике обычно ограничиваются заданием главной диагонали 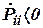 , то есть исходными дисперсиями ошибок оценивания, считая, что
, то есть исходными дисперсиями ошибок оценивания, считая, что 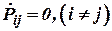 .
.
Со временем процесс решения уравнения ковариаций (рис. 2) приходит к установившемуся значению 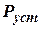 , при которой, выполняется равенство:
, при которой, выполняется равенство:
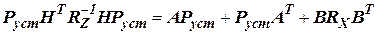
|
Со временем процесс решения уравнения ковариаций (рис. 2) приходит к установившемуся значению 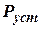 , при которой, выполняется равенство:
, при которой, выполняется равенство:
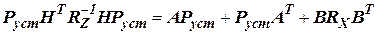
|
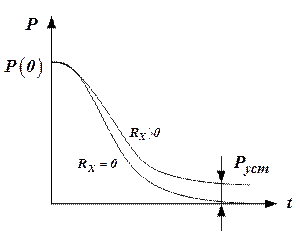
Рисунок 2
Задача оценки параметров заключается в нахождении компромисса при фильтрации помехи, спектр которой определен 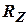 и полезным сигналом, спектр которого определен
и полезным сигналом, спектр которого определен 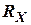 , с учетом динамических характеристик процесса, то есть матрицей коэффициентов системы ЛА.
, с учетом динамических характеристик процесса, то есть матрицей коэффициентов системы ЛА.
Заметим, что для устойчивой и детерминированной системы , то есть при отсутствии случайных возмущений (  ), всегда
), всегда 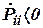 , а
, а 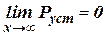 .
.
Таким образом, со временем ошибка в оценивании стремиться к нулю. При этом шумы измерителей не влияют на ошибку оценивания, поскольку сами измерители отключаются от схемы фильтра при 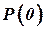 , и как следствие соответственно от уравнения коэффициентов коррекции
, и как следствие соответственно от уравнения коэффициентов коррекции 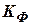 .
.
Во время синтеза фильтров этот эффект необходимо учитывать и до возмущения, что действует на ЛА, а так же учитывать и возможные неточности задания моделей процесса и измерения управления.
В уравнении коэффициентов коррекции (8) матрица 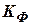 имеет вид:
имеет вид:
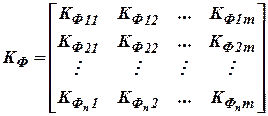
|
Элементы этой матрицы 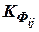 характеризует связь сигнала измерителя
характеризует связь сигнала измерителя 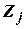 с оценкой координаты
с оценкой координаты 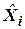 . Матрица наблюдений
. Матрица наблюдений 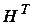 в уравнении коэффициентов коррекции определяет такой факт: если координата
в уравнении коэффициентов коррекции определяет такой факт: если координата 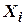 не берет участие в формировании сигнала
не берет участие в формировании сигнала 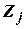 , то коэффициент
, то коэффициент 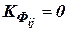 . Между коэффициентами
. Между коэффициентами 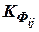 и
и 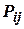 соответственно к уравнению коррекции существует прямая зависимость, что свидетельствует о том, что усиление коррекции оценок осуществляется сильнее в тех координатах, у которых больше предвидены ошибки оценивания, а противоположная зависимость коэффициентов
соответственно к уравнению коррекции существует прямая зависимость, что свидетельствует о том, что усиление коррекции оценок осуществляется сильнее в тех координатах, у которых больше предвидены ошибки оценивания, а противоположная зависимость коэффициентов 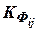 и
и 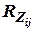 (в уравнении коррекции
(в уравнении коррекции 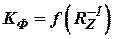 ) определяет более значимые сигналы коррекции от более точных измерителей.
) определяет более значимые сигналы коррекции от более точных измерителей.
Как вывод изобразим структурную схему алгоритма ОФК, который соответствует выше приведенным уравнениям (рис. 3).
Заметим, что поскольку при вычислении 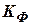 необходимо вычислить обратную матрицу
необходимо вычислить обратную матрицу 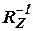 , то не для одного из измерителей нельзя задавать
, то не для одного из измерителей нельзя задавать 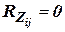 , а если такой измеритель существует, то необходимо искусственно задать незначительную величину
, а если такой измеритель существует, то необходимо искусственно задать незначительную величину 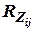 .
.
Дата добавления: 2015-08-14; просмотров: 1478;
