Пример. Применим ОФК к совместной обработке информации о продольной составляющей путевой скорости ЛА, то есть

Применим ОФК к совместной обработке информации о продольной составляющей путевой скорости ЛА, то есть 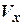, которая измеряется ИНС и ДИСС. Необходимо построить структурную схему ОФК и выбрать коэффициенты ОФК, которые обеспечат получение оптимальной оценки .

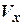С целью упрощения задачи допустим, что контролируемый процесс описывается уравнением 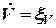, то есть матрица коэффициентов системы 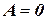. В качестве возмущения 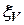принимаем белый шум со спектральной плотностью .

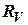Рисунок 3

Результаты измерений таковы:

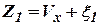- измерение при помощи ИНС;

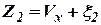- измерение при помощи ДИСС,

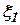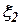где и - ошибки измерителей со спектральными плотностям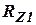и и 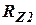соответственно.

Определим матрицу коэффициентов 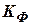для установившегося режима оценивания, то есть при 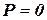. Тогда с учетом выше приведенных замечаний уравнения ОФК будут иметь вид:

;
;
,

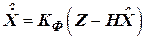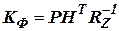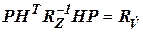где ; ; ; .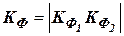

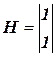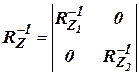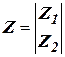Ковариационное уравнение в этом случае имеет вид:

.

В скалярном виде получим:

.

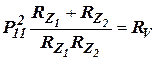Обозначим 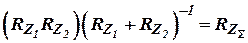и найдем дисперсию ошибок оценивания как

,

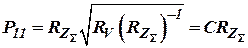где .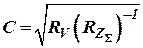

Запишем выражение для коэффициентов коррекции

,

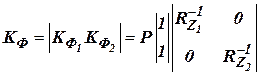или в скалярной форме

; ,

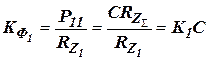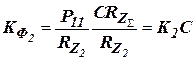где ;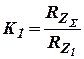

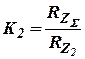
На рис. 4 показана структурная схема получения оценки для данного примера. Коэффициенты 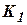и 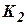отвечают оптимальным значениям, какие получают на этапе предварительного комплексирования измерителей. Поскольку сумма коэффициентов 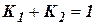, то схема фильтра, представленная на рис. 4 может быть преобразована в виде рис. 5.

Таким образом, для данной задачи показана возможность предварительного комплексирования измерителей без нарушения оптимального фильтра. Но для получения оптимальной оценки недостаточно просто использовать выход комплексного измерителя 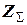, а необходим дополнительный фильтр в виде апериодического звена с постоянной времени. Оптимальный фильтр, учитывая характеристики контролируемого процесса, минимизирует ошибку оценивания.

.

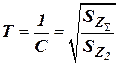Оптимальный фильтр, учитывая характеристики контролируемого процесса, минимизирует ошибку оценивания.

Рисунок 4

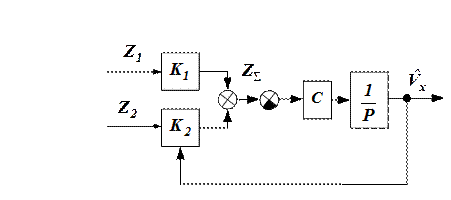
Рисунок 5