Теоремы Лагранжа и Ролля, их геометрическая интерпретация.
Теорема Лагранжа. Если функция 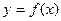 непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке 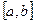 и дифференцируема во всех внутренних точках, то внутри отрезка существует по крайней мере одна такая точка
и дифференцируема во всех внутренних точках, то внутри отрезка существует по крайней мере одна такая точка 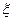 Î(а,b), в которой выполняется условие
Î(а,b), в которой выполняется условие
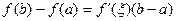 (8.2.1)
(8.2.1)
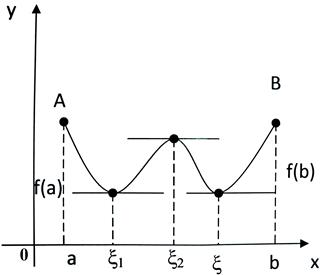
Проиллюстрируем геометрически выполнение теоремы.
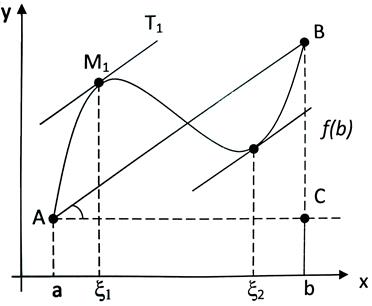
Проведем хорду АВ. Её угловой коэффициент

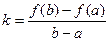

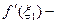 угловой коэффициент касательной М1Т1 в точке М1.
угловой коэффициент касательной М1Т1 в точке М1.
АВïçМ1Т1, следовательно
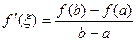 (8.2.2)
(8.2.2)
откуда и вытекает равенство.
Рис. 8.2.
Геометрическая формулировка теоремы Лагранжа. Если дана сплошная гладкая кривая, то на ней всегда существует точка (возможно, не единственная), касательная в которой параллельна хорде, стягивающей концы дуги.
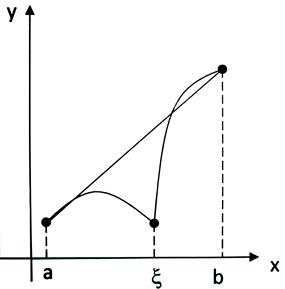 Механический смысл теоремы Лагранжа.
Механический смысл теоремы Лагранжа.
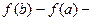 изменение функции на отрезке
изменение функции на отрезке 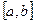 .
.
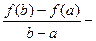 средняя скорость изменения функции на этом отрезке.
средняя скорость изменения функции на этом отрезке.
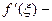 мгновенная скорость изменения функции.
мгновенная скорость изменения функции.
Рис. 8.3.
Если 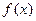 удовлетворяет условию теоремы Лагранжа, то внутри отрезка
удовлетворяет условию теоремы Лагранжа, то внутри отрезка 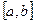 существует точка x, в которой скорость изменения функции равна средней скорости изменения функции на этом отрезке.
существует точка x, в которой скорость изменения функции равна средней скорости изменения функции на этом отрезке.
Замечание. Все требования теоремы Лагранжа существенны.
В точке x нарушено условие дифференцируемости (рис. 8.3).
Следствие (достаточный признак постоянства функции на отрезке). Если на некотором отрезке 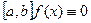 , то функция
, то функция 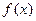 сохраняет на отрезке постоянное значение.
сохраняет на отрезке постоянное значение.
Пусть 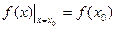 и
и 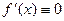
Для любого отрезка 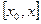 Î
Î 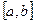 запишем теорему Лагранжа.
запишем теорему Лагранжа.
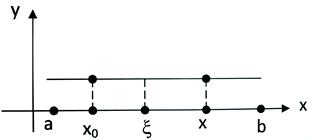
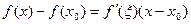
и 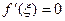 , следовательно, для любого
, следовательно, для любого 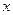 Î
Î 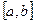
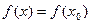 .
.
Рис. 8.4.
 Теорема Ролля
Теорема Ролля
Пусть функция 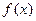 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
- 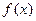 непрерывна на
непрерывна на 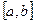 ;
;
- 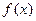 дифференцируема на
дифференцируема на 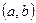 ;
;
- 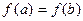 (рис.8.5.)
(рис.8.5.)
Тогда внутри отрезка (a,b) существует по крайней мере одна точка xÎ(а,b),в которой
Рис. 8.5. производная 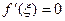 .
.
Доказательство автоматически вытекает из теоремы Лагранжа.
Геометрическая формулировка теоремы Ролля. Если дана сплошная гладкая кривая, концы которой равно стоят от оси Ох, то на кривой найдется хотя бы одна точка, касательная к кривой в которой параллельна оси Ох.
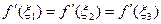
8.2.2. Правило Лопиталя (раскрытие неопределенностей вида 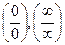 )
)
Теорема. Пусть функции 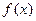 и
и 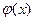 непрерывны и дифференцируемы в окрестности точки х0 (кроме, быть может, самой точки х0), обе одновременно стремятся к нулю или бесконечности и
непрерывны и дифференцируемы в окрестности точки х0 (кроме, быть может, самой точки х0), обе одновременно стремятся к нулю или бесконечности и  . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций
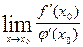
(конечный или бесконечный), то существует предел отношения функций, причем эти пределы равны, то есть, если существует
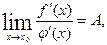 ,
,
то существует
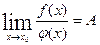
при этом
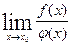 =
= 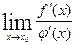 .
.
Дата добавления: 2015-08-14; просмотров: 586;
