Понятие дифференциала, его геометрический смысл, свойства.
Дифференциал функции.
Понятие дифференциала, его геометрический смысл, свойства.
Пусть функция 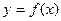 определена в точке
определена в точке 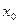 и дифференцируема в ней, то есть существует
и дифференцируема в ней, то есть существует
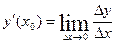 .
.
Следовательно 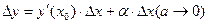 , представлено в виде суммы двух бесконечно малых.
, представлено в виде суммы двух бесконечно малых.
Сравним оба бесконечно малых слагаемых.
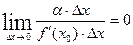 .
.
То есть 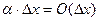 , это означает, что второе слагаемое бесконечно мало по сравнению с первым слагаемым
, это означает, что второе слагаемое бесконечно мало по сравнению с первым слагаемым 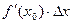 . Следовательно, если
. Следовательно, если 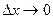 первое слагаемое (линейное относительно
первое слагаемое (линейное относительно 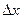 ) играет главную роль в приращении функции
) играет главную роль в приращении функции 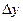 .
.
Главная линейная часть приращения функции называется дифференциалом функции и обозначается
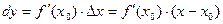 (8.1.1)
(8.1.1)
Пусть 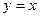 . Следовательно,
. Следовательно, 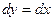 и
и 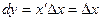 , откуда
, откуда 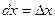 ,
,
 .
.
Так как  , то
, то 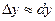 .
.
Если 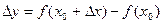 , то
, то 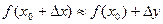 или
или
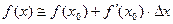 (8.1.2)
(8.1.2)
Представление функции в виде (8.1.2) называется линеаризацией функции.
Примеры:
1) 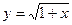
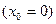 ,
, 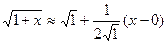 ,
, 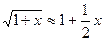 .
.
2) 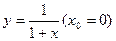 ,
, 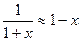 .
.
3) 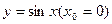 ,
, 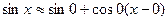 ,
, 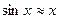 в окрестности точки
в окрестности точки 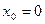 .
.
Дата добавления: 2015-08-14; просмотров: 506;
