ПЛОСКОСТИ И ПРЯМЫЕ, КАСАТЕЛЬНЫЕ К КРИВОЙ ПОВЕРХНОСТИ В ДАННОЙ ТОЧКЕ

Для построения плоскости, касательной к кривой поверхности в данной точки К, достаточно провести через эту точку на поверхности две пересекающиеся инструментально простые линии. Такими линиями могут быть две линии каркаса поверхности, например, параллель и меридиан на поверхности вращения.

Проведя касательные к каждой из этих кривых линий, получим две пересекающиеся прямые, определяющие одну и только одну плоскость t, касательную к данной поверхности в точке К, если данная точка является “гладкой точкой” поверхности.

Любая прямая лежащая в касательной плоскости и проходящая через точку касания К, будет касательной к заданной поверхности в этой точке.

Прямая n, проходящая через точку К и перпендикулярная к касательной плоскости t, являются нормалью поверхности в точке К.

На рис.12.6, для иллюстрации, через точку К проведены две кривые линии, принадлежащие некоторой выпуклой поверхности.

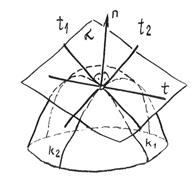
Рис.12. 6