ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ МЕСТ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ

Геометрическое место есть совокупность точек, положение которых удовлетворяет некоторым геометрическим условиям. Решение геометрических задач часто сводится к построению геометрических мест: требуется найти точки, линии и другие геометрические образы, удовлетворяющие тем или иным заданным условиям. Для каждого условия строится свое геометрическое место и затем берется сочетание этих геометрических мест.

Ниже перечисляются важнейшие геометрические места, к нахождению которых приводится решение многих задач.

1. Геометрическое место точек, равноудаленых от некоторой определенной точки, есть сфера с центром в этой точке.

2. Геометрическое место точек, равноудаленых от данных двух точек, есть плоскость, проходящая через середину отрезка, соединяющего данные точки, и к нему перпендикулярная.

3. Геометрическое место точек, равноудаленых от 3-х данных точек А, В и С, не лежащих на одной прямой, есть прямая, перпендикулярная к плоскости, определяемой тремя данными точками, и проходящая через центр окружности, описанной через эти три точки. Этот центр находится как точка пересечения плоскостей, проведенных через середины отрезков АВ, и ВС и соответственно к ним перпендикулярных.

4. Геометрическое место точек, равноудаленых от четырех данных точек А, В, С и D, не лежащих в одной плоскости, есть только одна точка - центр сферы, проходящей через эти точки. Этот центр находится как точка пересечения плоскостей, проведенных через середины отрезков АВ, ВС и СD и соответственно к ним перпендикулярных.

5. Геометрическое место точек, равноудаленых от данной прямой, есть поверхность прямого кругового цилиндра. Всякая плоскость, касательная к этому цилиндру, будет параллельна оси цилиндра и удалена от нее на данное расстояние.

6. Геометрическое место точек, равноудаленых от двух параллельных прямых, есть плоскость, перпендикулярная к отрезку, определяющему кратчайшее расстояние между данными прямыми и проходящая через его середину.

7. Геометрическое место точек, равноудаленых от трех параллельных прямых а, b и с не лежащих в одной плоскости, есть прямая, параллельная заданным прямым и являющаяся осью цилиндрической поверхности вращения, имеющая своими образующими эти прямые.

8. Геометрическое место точек, равноудаленых от двух пересекающих прямых, есть пара плоскостей, перпендикулярных к плоскости, содержащей данные прямые, и проходящей через биссектрисы углов между ними.

9. Геометрическое место прямых, проходящих через определенную точку на данной прямой и наклоненных к последней под заданным углом a⁰, есть поверхность прямого кругового конуса.

Если провести плоскость, пересекающую конус перпендикулярно к его оси, то поверхность конуса будет служить геометрическим местом прямых, проходящих через вершину и наклоненных к этой плоскости под углом 90⁰-a⁰.

Всякая плоскость, касательная к такому конусу, будет наклонена под углом 90⁰-a⁰ к этой плоскости нормального сечения конуса.

10. Геометрическое место точек, равноудаленых от данной плоскости, есть пара плоскостей, параллельных данной плоскости, есть пара плоскостей, параллельных данной плоскости и расположенных по разные от нее стороны на данном расстоянии.

11.Геометрическое место точек, равноудаленых от двух пересекающихся плоскостей, есть две биссекторные плоскости двугранных углов, образованных этими пересекающимися плоскостями. Каждая биссекторная плоскость проходит через линию пересечения плоскостей и делит пополам соответствующую пару углов между этими плоскостями.

12.Геометрическое место точек, равноудаленых от трех пересекающихся плоскостей a, b и g, есть прямая - линия пересечения плоскостей биссектора, равноделящих двугранные углы между плоскостями a и b и b и g.

ПРИМЕРЫ ПРИМЕНЕНИЯ СПОСОБА ГЕОМЕТРИЧЕСКИХ МЕСТ

Пример 1 (рис.12.14). Построить точку В по ее координатам у=m, z=n и R от точки А.

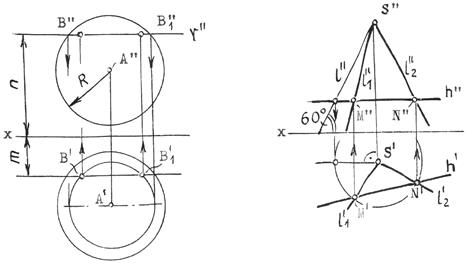
Рис.12.14 Рис.12.15

Пример 2 (рис.12.15). Через точку S провести прямую l, наклоненную к горизонтальной плоскости проекций под углом 60⁰ и пересекающую прямую h.

Литература:

1. Бубенников А.В. Начертательная геометрия: Учебник для втузов. - 3-е изд., перераб. и доп. - М.:Высш.шк., 1985, 288с.

2. Гордон В.О., Семенцев-Огиевский М.А. Курс Начертательной геометрии: Учеб. пособие (Под ред. Ю.Б.Иванова. -23 изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит., 1988, -272 с. ил.

3. Локтев О.В. Краткий курс начертательной геометрии: Учебник для втузов. - 2-е изд., перераб. и доп. -М:Высш.шк.,1985, 136 с.

4. Фролов С.А. Начертательная геометрия: Учебник для втузов. - 2-е изд., перераб. и доп. - М.: Машиностроение, 1989, 240 с.

5. Рыжов Н.Н. Образование поверхностей и их задание на комплексном чертеже. Метод. указан. по курсу начертательной геометрии. Изд.МАДИ, -М.: 1983.

6. Рыжов Н.Н. Главные позиционные задачи. Метод.указан. по курсу начертательной геометрии. Изд МАДИ, М.: 1984.

7. Рыжов Н.Н. Метрические задачи. “Преобразование комплексного чертежа”. Метод. указан. по курсу “Начертательная геометрия”. Изд. МАДИ. -М.: 1985.