ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С КРИВОЙ ПОВЕРХНОСТЬЮ

При построении точек пересечения прямой линии с кривой поверхностью вспомогательную секущую плоскость стараются выбрать таким образом, чтобы она пересекла кривую поверхность по линии, легко определяемой на чертеже, то есть по инструментально простой линии: прямой или окружности. Алгоритм решения:

1. Заданную прямую заключают во вспомогательную секущую плоскость (чаще проецирующую);

2. Строят сечение заданной поверхности этой плоскостью;

3. Находят общие точки фигуры сечения с заданной прямой;

4. Определяют видимость прямой линии относительно поверхности. В этом случае можно воспользоваться конкурирующими точками.

Пример 1 (рис.10.27). Найти точки пересечения прямой l с поверхностью конуса.

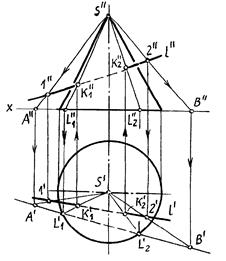
Рис.10.27

На рис.10.27 вспомогательная секущая плоскость проведена через прямую l и вершину S конуса. Она пересекла конус по образующим SL₁ и SL₂. Вспомогательная секущая плоскость задана прямыми S1 и S2, а ее горизонтальный след - линия АВ.

Задачи на взаимное пересечение прямой линии с кривой поверхностью - задачи третьего типа могут быть сведены к задачам второго типа путем преобразования комплексного чертежа.

Пример 2. (Рис. 10.28) Найти точки пересечения прямой l с поверхностью сферы. Прямая l занимает общее положение.

Решение легко находится после преобразования чертежа, после которого прямая l преобразуется в прямую уровня (фронталь).

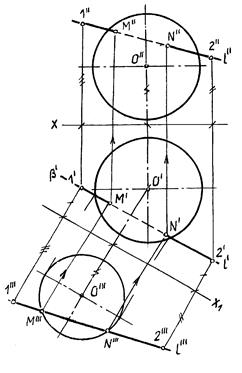
Рис.10.28

Пример 3. (рис.10.29). Найти точки M и N пересечения прямой l с цилиндрической поверхностью вращения. Решение:

Преобразуем заменой плоскостей проекций чертеж так, чтобы цилиндрическая поверхность стала проецирующей. Одновременно с этим прямая l (1,2) преобразуется в линию l^IV(1^IV,2^IV), точки пересечения которой с очерком цилиндрической поверхности - M^IV и N^IV и будут искомыми. Обратным преобразованием найдем эти точки на исходных проекциях. Построения ясны из чертежа.

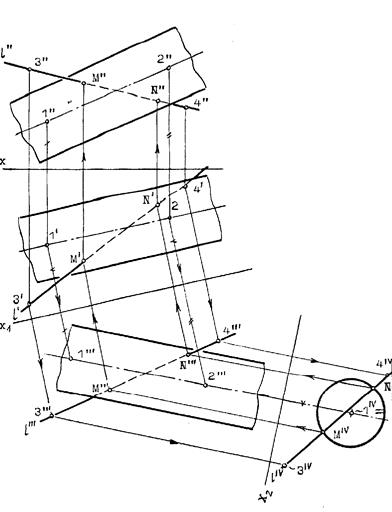
Рис.10.29