РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ

Кривые поверхности, которые полностью, без растяжения или сжатия, без разрывов и складок можно совместить с плоскостью, называют развертываемыми. К этим поверхностям относятся лишь линейчатые и только такие, у которых смежные образующие пересекаются между собой или параллельны. Этим свойством обладают торсы (поверхности, образованные прямыми, касательными к направляющей пространственной кривой), конические и цилиндрические поверхности. Остальные линейчатые поверхности, а также все не линейчатые - являются не развертываемыми.

Построение полной развертки прямого кругового усеченного цилиндра вращения

(рис. 10.41).

Для построения развертки цилиндра достаточно представить его как призму с большим количеством граней (фактически достаточно 12-16 таких граней), равномерно разделив окружность основания цилиндра на равное число частей.

Рис.10.41

Если на поверхности цилиндра расположена какая-либо линия, то на развертку цилиндра эту линию можно перенести по точкам, принадлежащим соответствующим образующим этой поверхности.

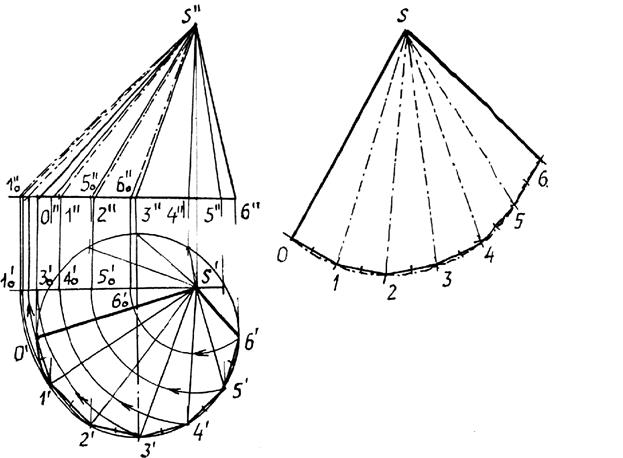
Построения развертки полной поверхности прямого кругового конуса (рис.10.42).

Для построения развертки прямого кругового конуса достаточно представить его поверхность как правильную пирамиду с большим числом граней и далее построить ее развертку, найдя натуральную величину одной из граней, представляющей собой равнобедренный треугольник, по его боковой стороне и основанию. Построение развертки конуса видно из чертежа, где основание “грани” S01 равно хорде 0<sup>`</sup>1`. Развертка боковой поверхности конуса, в данном случае, содержит 12 таких “граней”.

Развертка боковой поверхности будет найдена точнее, если определить угол j⁰ при точке S на развертке по формуле:

j⁰=R/l 360⁰, где R - радиус основания конуса, а l - длина образующей конуса.

Рис.10.42

Принадлежащие боковой поверхности конуса точки некоторой кривой АВСDЕ можно найти по принадлежности этих точек соответствующим образующим конической поверхности. Для этого достаточно способом вращения, как показано на примере точки С, принадлежащей образующей S2, найти отрезки S``B``₀=SB, S``D``₀=SD и S``E``₀=SE ... Найденные отрезки отложить по соответствующим образующим на развертке конуса и провести через них линию АВСDE. Для получения полной развертки поверхности конуса ее нужно дополнить основанием конуса, касательным в соответствующей точке развертки боковой поверхности.

Развертка боковой поверхности наклонного конуса находиться как развертка наклонной пирамиды с большим количеством граней, каждую из которых находят по трем сторонам - двум боковым “ребрам” и “основанию”.(рис.10.43).

Отсек поверхности наклонного кругового конуса и его развертка.

Рис.10.43

При построении развертки необходимо обратить внимание на то, чтобы внешняя поверхность конуса на развертке была обращена наружу, к наблюдателю.