АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

1.Общие замечания.

При построении комплексного чертежа предмета последний обычно располагают так, чтобы направления трех главных измерений его были параллельны плоскостям проекций: направление длины - параллельно оси х, ширины - оси y и высоты - оси z.

Тогда длина и высота проецируются в натуральную величину на фронтальную плоскость проекций, длина и ширина не искажаются на горизонтальной проекции, а ширина и высота - на профильной.

Такой чертеж нетрудно строить, по нему просто производить измерения, судить о размерах изображаемого предмета. Однако, он недостаточно нагляден. На каждой из проекций отсутствует одно из трех измерений. Чтобы воспроизвести форму предмета, надо мысленно воссоздать ее по двум, трем, а иногда и большему числу проекций.

Более наглядный чертеж можно получить, проецируя предмет на одну плоскость проекций и располагая его так, чтобы ни одно из направлений главных измерений не проецировалось точкой.

2. Чтобы образовать аксонометрический чертеж некоторой фигуры, например, точки А, необходимо жестко связать эту фигуру с некоторой декартовой системой координат 0хyz. При этом на координатных осях: 0х, 0y, и 0z зададим единую определенную натуральную единицу измерения е (в мм, см и тому подобное).

Так как точка А жестко связана с натуральной системой координат, то можно построить ее проекции на любую координатную плоскость. Например, построить проекцию А` точки А на плоскость p<sub>1</sub>(0хy). После этого точку А и ее проекцию А` и натуральные координатные оси параллельно проецируем на плоскость аксонометрического чертежа p₀ по направлению s (рис.11.1).

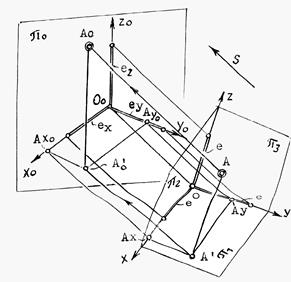
Рис.11.1

Полученную совокупность проекций (А₀, А`₀, х₀, y₀ и z₀) на p₀ будем называть аксонометрическим чертежом заданной фигуры - точки А,

Прямые х₀, y₀ и z₀ называются аксонометрическими осями.

Проекция А₀ называется главной аксонометрической проекцией точки А, а проекции А`₀ - вторичной. Очевидно, на полученном чертеже могут быть построены и другие вторичные проекции точки А: А``₀ и A```₀.

3. Отношение длины аксонометрического координатного отрезка 0₀Ах₀ к длине натурального координатного отрезка 0Ах называется показателем искажения по оси 0₀х₀ и обозначается буквой u: u=0₀Ax₀: 0Ах. Иначе, е_х: е=u.

Такой же смысл имеют показатели искажения e_y и e_z:

v=0₀Ay₀: и w=0₀Ax₀:0A_z.

Показатели искажения по осям в общем случае различны:

u¹v¹w¹u. В частном случае, когда u=v=w акснометрический чертеж называют изометрическим чертежом или короче - изометрией.

Если показатели искажения по двум осям равны между собой, а по третьей оси показатель искажения отличается от первых двух (u=w¹v и т.п.), то чертеж называется диметрическим, или кратко, - диметрией.

В общем случае, когда u¹v¹w, то такой чертеж называют триметрией.

4.Основная теорема аксонометрии - торема Польке (1851), утверждает:

Любые три отрезка на плоскости, исходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных пространственных отрезков.

В зависимости от направления параллельного проецирования по отношению к плоскости аксонометрического изображения различают косоугольные и прямоугольные аксонометрические проекции.

Между показателями искажения и углом наклона проецирования по отношению к плоскости аксонометрического изображения существует зависимость: u²+v²+w²=2+ctg²j.

Для прямоугольной аксонометрической проекции угол j=90⁰, следовательно: u²+v²+w²=2. Где:

1<u²+v²<2 и 1<u²+w²<2.

Теорема Вейсхбаха (1840):

Оси прямоугольной аксонометрической проекции являются биссектрисами углов треугольника, стороны которого пропорциональны квадратам коэффициентов искажения.

Таким образом, зная коэффициенты искажения некоторой прямоугольной аксонометрической проекции, можно найти ее аксонометрические оси (рис.11.2)

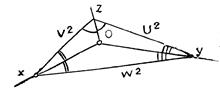
Рис.11.2

5.Построение осей и коэффициентов искажения прямоугольной аксонометрической проекции по треугольнику следов.

Если плоскость аксонометрической проекции пересекает плоскости пространственной системы координат, то фигурой сечения будет остроугольный треугольник XYZ - треугольник следов: XY, XZ и YZ. Оси пространственной системы координат спроецируются на плоскость аксонометрического изображения - высотами этого треугольника (совпадут с направлениями высот данного треугольника) (рис.11.3) и (рис.11.4).

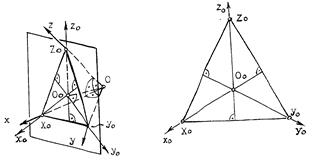
Рис.11.3 Рис.11.4

Если задано направление аксонометрических осей Ox, Оy и Оz, то, построив произвольный треугольник следов, можно найти величины коэффициентов искажения по этим осям, задавшись величиной единичного отрезка е (рис.11.5).

Решение:

1.Строим треугольник следов (произвольный);

2. Находим совмещенное положение треугольников XOY и XOZ с плоскостью аксонометрического изображения. Получаем XOY и ZOY.

3. Отложив на направлении OX, OY и OZ отрезки равные e (единичный масштаб), находим его проекции: е_х, е_y и е_z на аксонометрических осях.

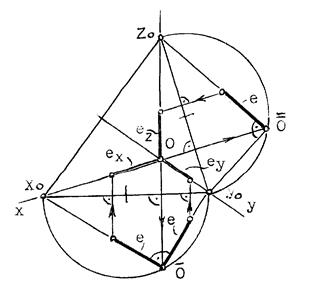
Рис.11.5