ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ

Для построения линий взаимного пересечения двух кривых поверхностей пользуются методом вспомогательных секущих поверхностей. В качестве, которых используются не только вспомогательные секущие плоскости, но и вспомогательные секущие поверхности: цилиндрические, конические и сферы, выбор которых в качестве “посредников” позволяет находить точки искомой линии пересечения.

1. Возможности применения способа вспомогательных секущих плоскостей в качестве “посредников”.

Вспомогательные секущие плоскости применимы, если заданы:

- две поверхности вращения, оси которых перпендикулярны к одной из плоскостей проекций;

- два цилиндра или два конуса, или конус и цилиндр;

- две линейчатые поверхности с общей плоскостью параллелизма;

- две каркасные поверхности.

Пример 1(рис.10.30). Построить линию пересечения сферы с конусом.

Решение: 1. Находим характерные и опорные точки искомой линии пересечения. Такими точками будут точки пересечения очерковых образующих: А, В, С и С₁. Точки С и С₁ получены с помощью вспомогательной секущей плоскости g, проходящей через экватор сферы. 2. Промежуточные точки искомой линии находим с помощью семейства вспомогательных секущих плоскостей: g₁, g₂,... 3. Соединяя последовательно найденные точки А, М, С, N,..В получаем проекции искомой линии. 4. Определяем видимость.

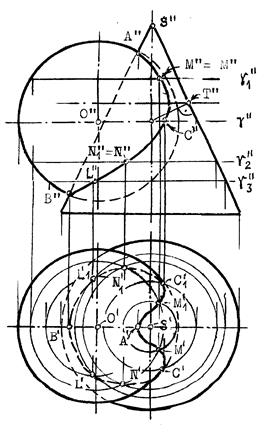
Рис.10.30

Пример 2 (рис.10.31). Построить линию взаимного пересечения поверхностей цилиндра и тора.

Решение:

Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций и потому точки искомой линии пересечения можно найти с помощью вспомогательных секущих плоскостей: b, b₁, b₂,...

Построение начинаем с опорных точек А и В искомой линии, принадлежащих очерковым образующим.

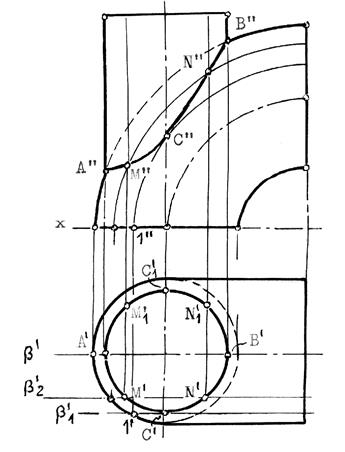
Рис.10.31

2. Возможности применения вспомогательных секущих сфер в качестве “посредников”.

Применение вспомогательных секущих сфер возможно в следующих случаях, когда на чертеже заданы:

1. Две поверхности вращения, оси которых пересекаются и параллельны одной из плоскостей проекций;

2. Две поверхности вращения, оси которых пересекаются, но ось одной из них параллельны, а ось другой - перпендикулярна к одной и той же плоскости проекций.

3. Когда на чертеже заданы две поверхности с общей плоскостью симметрии и одна из них является поверхностью вращения, а другая поверхность имеет семейство плоских круговых сечений, перпендикулярных общей плоскости симметрии.

Рассмотрим эти случаи на примерах.

Если на чертеже заданы две поверхности вращения, оси которых пересекаются и параллельны плоскости чертежа, то точки искомой линии пересечения могут быть найдены с помощью вспомогательных секущих концентрических сфер с центром в точке пересечения осей.

Пример 1 (рис.10.32). Построить линию пересечения поверхности конуса вращения с тором.

Решение:

Из точки О пересечения осей опишем некоторую сферу радиуса R. Она пересечет конус по двум параллелям: 1-1 и 2-2, а тор - по 3-3. Общие точки Е и Е пересечения параллелей 1-1 и 3-3 будут точками искомой линии пересечения заданных поверхностей.

По аналогии, описывая новые сферы, получим необходимое и достаточное количество точек искомой линии пересечения.

Примечание.

Сфера минимального радиуса R₁ будет касаться одной из поверхностей вращения и пересекать другую. В данном случае, она касается конуса и пересекает тор по параллели 4-4.

Точки С и С₁ получены с помощью вспомогательной горизонтальной плоскости g, проведенной через ось тора.

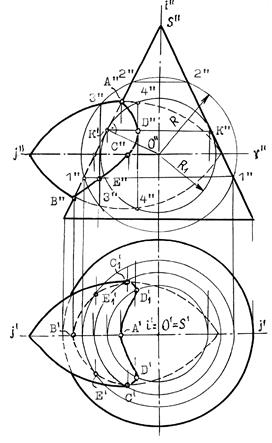
Рис.10.32

Идея применения способа вспомогательных секущих сфер основана на свойстве взаимного пересечения двух соосных поверхностей вращения, то есть имеющих общую ось вращения, по общим для них параллелям (рис.10.33).

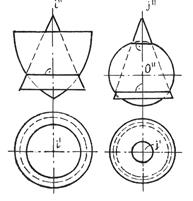
Рис.10.33

Пример 2 (рис.10.34). Построить линию взаимного пересечения поверхностей конуса и тора.

Решение:

В данном случае ось конуса параллельна, а ось тора - перпендикулярна горизонтальной плоскости проекций. Поэтому очерки вспомогательной секущей сферы некоторого радиуса Р нужно провести из точки О пересечения осей заданных поверхностей на той и другой плоскостях проекций. При этом на фронтальной проекции фигур сфера пересечет тор по параллели 1-1, а на горизонтальной плоскости проекций эта же сфера пересечет конус по параллелям 2-2 и 3-3. Поскольку окружность 1-1 проецируется на горизонтальную плоскость проекций в истинную величину, а параллели конуса - в прямые линии, то точки М и М пересечения этих линий и будут искомыми точками линии пересечения.

Аналогично можно найти необходимое и достаточное количество точек для построения проекций линии пересечения поверхностей.

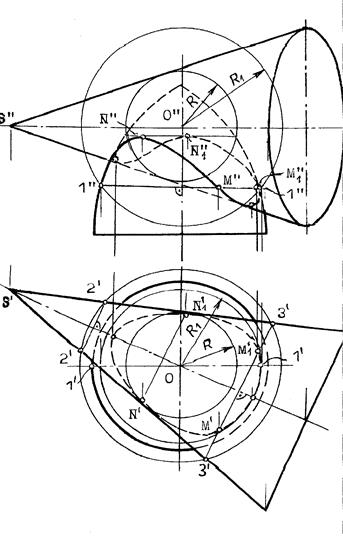
Рис.10.34

Пример 3 (рис.10.35). Построить линию взаимного пересечения поверхностей двух торов.

Решение: Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Причем открытый (тор-кольцо) имеет семейство круговых сечений, перпендикулярных плоскости симметрии. Это третий из рассматриваемых случаев, когда невозможно применение вспомогательных секущих сфер в качестве “посредников”.

Нахождение точек искомой линии пересечения заданных поверхностей начинаем с определения опорных точек А и В, в интервале между которыми расположится искомая линия пересечения поверхностей. Выбираем на поверхности тора-кольца произвольное круговое сечение 1-1, лежащее в плоскости, проходящей через ось j вращения тора-кольца. Из центра С₁ восставим перпендикуляр к линии 1-1, который пересечет ось второго тора в точке О₁. Из точки О₁ опишем сферу радиуса О₁-1, пересекающую второй тор по окружности 2-2. Общие точки М и М₁ окружностей 1-1 и 2-2 и будут точками искомой линии пересечения заданных поверхностей. Таким же способом найдены точки N и N₁ и другие не указанные точки.

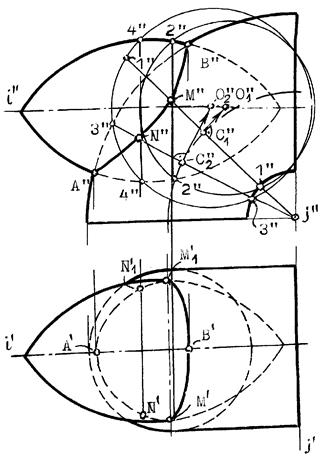
Рис.10.35