ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

Две поверхности второго порядка пересекаются по кривой четвертого порядка. На общую плоскость симметрии поверхностей кривая их пересечения проецируется кривой второго порядка. Если часть кривой пересечения двух поверхностей второго порядка есть кривая второго порядка, то другая часть - также линия второго порядка (в том числе могут быть и пары прямых).

Через две линии второго порядка, лежащие на одной поверхности второго порядка, можно провести другую поверхность второго порядка.

Теорема Монжа: две поверхности второго порядка, описанные вокруг третьей поверхности второго порядка или вписанные в нее, пересекаются между собой по двум кривым второго порядка.

Значит, в этом случае пространственная кривая распадается на пару плоских кривых (рис.10.36).

Если две поверхности второго порядка имеют две общие соприкасающиеся с ними плоскости, то линия их пересечения распадается на пару кривых второго порядка (рис.10.37).

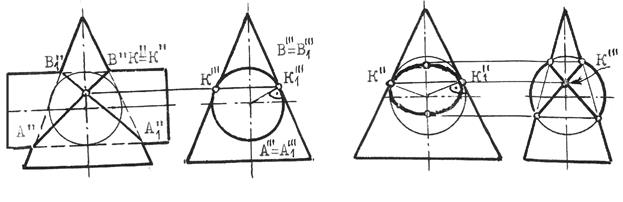
Рис.10.36 Рис.10.37

Проекция сечения эллипсоида вращения на плоскости, перпендикулярной к его оси, является эллипс, большая ось которого перпендикулярна к плоскости общей симметрии (рис.10.38).

Проекция эллиптического сечения однополостного гиперболоида вращения на плоскости, перпендикулярной к его оси, является эллипс, малая ось которого перпендикулярна общей плоскости симметрии поверхности (рис.10.39).

Проекция эллиптического сечения параболоида вращения на плоскости, перпендикулярной к его оси вращения, есть окружность (рис.10.40).

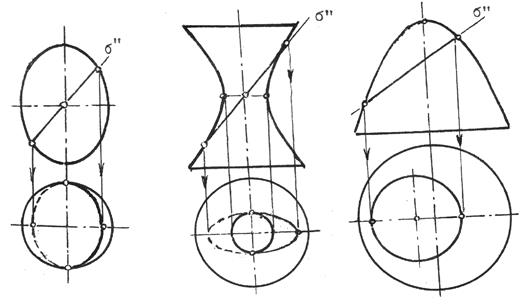
Рис.10.38 Рис.10.39 Рис.10.40