Линейные и билинейные функции на линейном пространстве
1°. Определение функции. Линейные функции.
Определение 1. Будем говорить что, на линейном пространстве 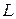 задана функция (от одного вектора), если
задана функция (от одного вектора), если 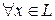 поставлено в соответствие число. Будем говорить, что на
поставлено в соответствие число. Будем говорить, что на 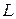 задана функция двух векторов, если
задана функция двух векторов, если 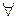 упорядоченной паре
упорядоченной паре 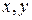 поставлено в соответствии число.
поставлено в соответствии число.
Обозначение: 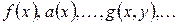 .
.
Замечание 1. Функции на бесконечно мерных пространствах принято называть функционалами.
Замечание 2. Обычно под функцией понимают величину инвариантную относительно замены базиса, т.е. такую, что она не меняется при переходе от одного базиса к другому. А именно, если 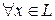 в базисе
в базисе 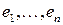 ставится в соответствие первая координата, то это не функция, так как зависит от выбора базиса.
ставится в соответствие первая координата, то это не функция, так как зависит от выбора базиса.
Пусть 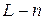 –мерное линейное пространство, и в нем задан некоторый базис. Тогда
–мерное линейное пространство, и в нем задан некоторый базис. Тогда 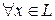 определяется
определяется 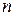 координатами
координатами 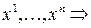 функция при фиксированном базисе задаётся как обычная функция n переменных. При переходе к другому базису она изменяется.
функция при фиксированном базисе задаётся как обычная функция n переменных. При переходе к другому базису она изменяется.
Определение 2. Функция 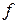 , заданная на линейном пространстве
, заданная на линейном пространстве 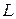 , называется линейной, если
, называется линейной, если
1. 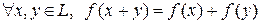 ,
,
2. 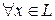 ,
, 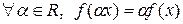 .
.
Дата добавления: 2015-08-14; просмотров: 696;
