Пример. 1°. Если , , то – линейная функция.
1°. Если 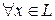 ,
, 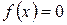 , то
, то 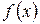 – линейная функция.
– линейная функция.
2°. Если 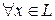 ,
, 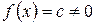 , то эта функция не является линейной.
, то эта функция не является линейной.
Пусть 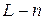 –мерное линейное пространство и
–мерное линейное пространство и 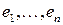 – фиксированный базис
– фиксированный базис 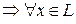 может быть записан в базисе
может быть записан в базисе  . Значение функции
. Значение функции 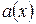 может быть записано в базисе:
может быть записано в базисе:
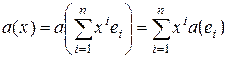 .
.
Здесь числа 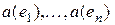 не зависят от выбора
не зависят от выбора 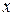 , а определяются лишь базисом. Таким образом, доказано следующее утверждение.
, а определяются лишь базисом. Таким образом, доказано следующее утверждение.
Лемма 1.Каждая линейная функция на 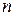 –мерном линейном пространстве в произвольном базисе
–мерном линейном пространстве в произвольном базисе 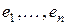 задаётся линейным однородным многочленом
задаётся линейным однородным многочленом
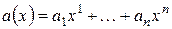
| (1) |
от компонент вектора по этому базису. Коэффициенты 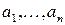 многочлена (1) есть значения функции на базисных векторах.
многочлена (1) есть значения функции на базисных векторах.
Часто вместо линейной функции говорят линейные формы!
Числа 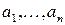 будем называть компонентами (коэффициентами) функции
будем называть компонентами (коэффициентами) функции 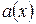 в базисе
в базисе 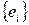 . Итак,
. Итак, 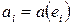 .
.
Формулу (1) можно записать в виде
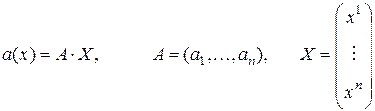 .
.
Выясним, как меняются компоненты функции 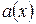 при переходе к новому базису. Пусть
при переходе к новому базису. Пусть 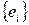 и
и 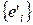 связаны формулами перехода
связаны формулами перехода 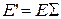
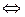
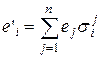 .
.
Тогда
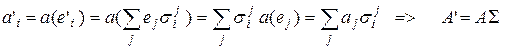 , ,
| (2) |
то есть компоненты линейной функции преобразуются также как и базисные векторы.
Покажем, что такое преобразование компонентов линейной функции обеспечивает инвариантность её значений. Напомним, что если 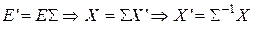 .
.
Тогда 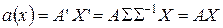 , т.е. численное значение функции при изменении базиса сохраняется.
, т.е. численное значение функции при изменении базиса сохраняется.
2°. Билинейные функции на линейном пространстве.
Определение 3. Билинейной функцией (или билинейной формой) 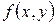 на линейном пространстве
на линейном пространстве 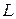 называется функция
называется функция 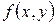 от двух векторов
от двух векторов 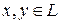 :
:
1°. При фиксированном 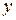 ,
, 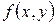 – линейная функция
– линейная функция 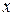 ;
;
2°. При фиксированном 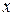 ,
, 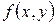 – линейная функция
– линейная функция 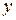 .
.
Иными словами,
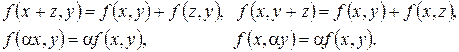
Примеры:
1°. Рассмотрим пространство 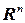 и пусть
и пусть 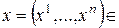
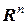 . Положим
. Положим
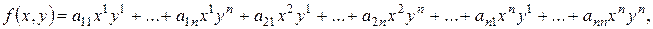 где
где 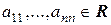 . Очевидно, что это билинейная форма.
. Очевидно, что это билинейная форма.
2°. Пусть 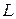 – пространство
– пространство 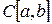 и
и 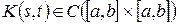 .
.
Положим 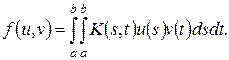 Это билинейная форма. Если
Это билинейная форма. Если 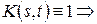
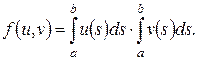
Задача. Показать, что если 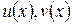 – линейные функции, то
– линейные функции, то 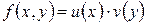 – билинейная.
– билинейная.
Пусть 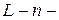 мерное линейное пространство с базисом
мерное линейное пространство с базисом 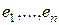 .
.
Если 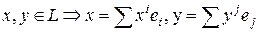 , то билинейная функция
, то билинейная функция 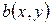 может быть вычислена следующим образом:
может быть вычислена следующим образом:
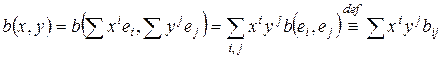 .
.
Здесь 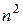 чисел
чисел 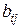 являются значениями билинейной формы на всевозможных парах базисных векторов и называются коэффициентами билинейной формы в базисе
являются значениями билинейной формы на всевозможных парах базисных векторов и называются коэффициентами билинейной формы в базисе 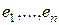 . Если ввести матрицу билинейной формы, то есть матрицу
. Если ввести матрицу билинейной формы, то есть матрицу 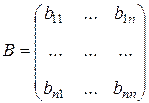 , то
, то
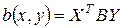 . (3)
. (3)
Рассмотрим изменение матрицы 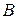 при переходе к другому базису.
при переходе к другому базису.
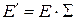 , то есть
, то есть 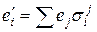 Þ
Þ 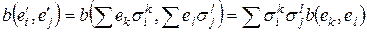 Þ
Þ
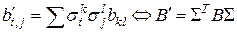 , (4)
, (4)
где 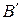 – матрица билинейной функции в базисе
– матрица билинейной функции в базисе 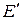 .
.
Определение 4. Билинейная форма 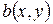 называется симметричной, если
называется симметричной, если 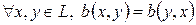 .
.
Если билинейная форма симметрична, то 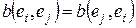 Þ матрица билинейной формы симметрична.
Þ матрица билинейной формы симметрична.
Обратно, пусть матрица билинейной формы симметрическая, то есть
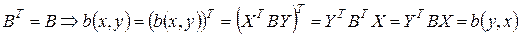 , то есть билинейная форма тоже симметричная. Итак,
, то есть билинейная форма тоже симметричная. Итак,
Предложение. Билинейная форма симметрична Û её матрица – симметрическая (в произвольном базисе).
Дата добавления: 2015-08-14; просмотров: 590;
