Жиындардың Декарт көбейтіндісі

х₁...х_n n элементтен тұратын реттелген тізбекті (x₁,x₂,…,x_n) немесе <x₁,x₂,…,x_n> деп белгілеуге болады. Мұндағы дөңгелек, бұрышты жақшалар элементтердің жазылу ретін көрсету үшін ғана қолданылады. Мұндай нөмірлерінің ретіне қарай орналасқан тізбек ұзындығы реттелген тізбек немесе ұзындығы n болатын кортеж деп аталады. 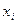-элемент <x₁,x₂,…,x_n> кортежінің і- координатасы деп аталады.

Мысалдар

{a,b,c} және {1,2} жиындарынан ұзындығы 2-ге тең 6 кортеж құруға болады:

(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)

2. Кез-келген әріптерден құралған сөз кортеж, натурал сандардың ондық жүйедегі жазылуы цифрлардан тұратын кортеж т. б.

Кез-келген координаттары әртүрлі реттелген ақырлы жиын кортеж.Ұзындығы 2-ге тең кортеждер реттелген жұптар, ұзындығы 3-ке тең кортеждер реттелген үштіктер, ұзындығы n-ге реттелген n-діктер деп аталады. Жиындар екі элементпен алу амалының көмегімен төмендегі ережеге сәйкес кодталады.

< >⇋Æ, <x₁> ⇋x₁, <x₁, x₂>⇌{{x₁},{x₁,x₂}}, <x₁,…,x_n>⇌< <x₁,x₂,…,x_n>, x_n+1 >

Анықтама.Екі кортеж ұзындықтары бірдей, әрі бірдей нөмірлі координаттары тең болса ғана тең болады. Яғни x=(x₁,x₂,…,x_n) , y=(y₁,y₂,…,y_n) кортеждері x₁=y₁; x₂=y₂,…x_n=y_n болғанда ғана тең болады

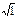
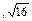
( x=y ). Мысалы (1², 2² , 3² ) және ( 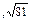) кортеждері тең. (1,2,3) және (3,1,2) әртүрлі ; (1,2,3) және (1,2,3,4) әртүрлі; (1,2)¹(2,1) ал {1,2} және {2,1} жиындары тең. Кортеждердің координаттары жиын, кортеж т. б. болуы мүмкін. Мысалы, ({a,b},c)=({b,a},c) себебі {a,b}={b,a}, ал ( (a,b ), c ) және ( (b,a), c ) кортеждері тең емес, себебі (a,b)¹(b,a). Бір де бір координаты жоқ кортеж (ұзындығы 0) бос кортеж деп аталады.

Сонымен жиын мен кортеж ұғымдарының айырмашылығы:

а) жиындардың элементтерінің орны, реті бәрі бір, ал кортеждерде элементтерінің ұзындығы бірдей болып элементтерінің реті басқаша болса тең емес (құрамы бірдей болса да);

б) жиында элементтер әртүрлі, кортежде бірдей бола береді.

Анықтама. А және В жиындарының тура( декарт) көбейтіндісі деп элементтері реттелген (х ,у) жұбынан тұратын жиынды айтамыз.Мұндағы, хÎА, ал уÎВ. Декарт көбейтіндісі әр түрлі жиын элементтерінен құралады, А ´ В болып белгіленеді: А ´ В = {(х ,у) | хÎА және уÎВ}.

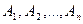жиындары үшін Декарт көбейтіндісі?

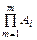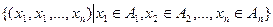= = болады.

Егер A₁=A₂=…=A_n=A болса, онда A₁хA₂х,…,хA_n жиыны А жиынының n-ші Декарт дәрежесі деп аталады және Аⁿ болып белгіленеді. Анықтама бойынша A⁰⇌{Æ}

Мысалдар:

1.A={1,2}, B={3,4} берілсін. AхB={ (1,3),(1,4),(2,3),(2,4) };

BхA={ (3,1),(3,2),(4,1),(4,2) };

AхA={ (1,1),(1,2),(2,1),(2,2) }; Бұл мысалдардан AхB¹BхA.

2. (Шахмат тақтасы).

A={a,b,c,d,e,f,g,h}; B={1,2,3,4,5,6,7,8} жиындары берілсін. Олай болса әр (х,у) жұбына x,yÎAхB шахмат тақтасының торлар жиыны сәйкес келеді.

3. [0,1]² жиыны { (a,b) | 0 £ a £1, 0 £ b £ 1 } ;Бұл жиынға жазықтықтың 1-ден аспайтын теріс емес координаттары бар нүктелер жиыны сәйкес келеді.

4. A={a,b,c}; B={1,2}; AхB={(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)}; BхA={(1,a),(2,a),(1,b),(2,b),(1,c),(2,c)}; AхB ¹ BхA

5. А={1,2,3}; АхА={(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1 ), (3,2), (3,3) };

6. 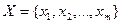; ; 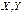- жиындарының Декарт көбей-тіндісін табайық. Декарт көбейтіндісінің элементтері әр түрлі жиын элементтерінен алынған жұптардан тұратындығы белгілі.

Оларды кестеге орналастырайық: Бұл кестеде m жол, n бағаннан тұратын элементтер жұбын көреміз. 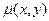- саны х-элементтерінің жиыны мен ү элементтерінің жиындарының көбейтіндісіне тең. 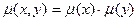(1)

Бұл жиындарды көбейту ережесі. Егер декарт көбейткіштері n жиыннан тұрса, онда (1) төмендегідей жалпылауға болады:

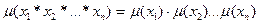(2)A х B х C; (A х B) х C; A х (B х C) жиындары да әр түрлі. A х B х C- (a,b,c); (A х B) х C-

((a,b),c ) aÎA, bÎB, cÎC; A х (B х C)=(a, (b,c) ); Егер А,В жиындарының бірі бос болса, олардың Декарт көбейтіндісі де бос деп есептеледі. A х Æ = Æ х A = Æ х Æ = Æ;

Мысал, А={a₁,a₂,a₃}, B={b₁,b₂,b₃} ; ;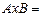

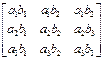Негізгі әдебиет: 1[5-9]; 2[10-16]

Қосымша әдебиет: 7[9-34]

Бақылау сұрақтары:

1. Қандай жиынды ішкі жиын деп атайды?

2. Қандай жиындар тең болады?

3. Жиындармен орындалатын негізгі операцияларды қандай?

4. Бірігу,қиылысу,толықтыру операцияларының негізгі қасиеттерін атаңыз.

5. Жиындарды өрнектеудің қандай әдістері бар?

2-Дәріс. Сәйкестік және оның қасиеттері Функциялар мен бейнелеулер. 2 сағ)

Дәріс конспектісі. Сәйкестіктер – жиын элементтерінің арасындағы өзара байланысты беру тәсілі. Оның дербес жағдайлары: функциялар, бейнелер, түрлендірулер, т.б.

Анықтама. А, В жиындарының арасындағы сәйкестік деп бұл жиындардың тура (декарт) көбейтіндісінің G ішкі жиынын айтады.

G ÍAхB Егер (a,b)ÎG болса,G сәйкестігінде b a-ға сәйкес деп айтады. d_G={a|(a,b)ÎG, G сәйкестігінің анықталу облысы, ал r_G={b|(a,b)ÎG} мәндер жиыны деп аталады.

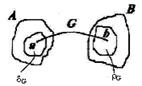Анықтама. Егер d_G=A болса толық анықталған сәйкестік, d_AÍA болса толық емес (жартылай) сәйкестік болады. (толық анықталмаған).

Анықтама.Егер r_G=B – сюръективті сәйкестік деп аталады. (В-ның әрбір элементінің А прообразы бар) Анықтама А жиынының әрбір aÎA элементіне B жиынының G сәйкестігіндегі а-ға сәйкес барлық bÎB элементтерінің жиыны a элементі- нің образы, ал әрбір bÎB элементіне А жиынының G сәйкестігіндегі в-ға сәйкес барлық aÎA элементтерінің жиыны b элементінің А жиынындағы прообразы деп аталады.

Анықтама. Барлық аÎ С Ír_Gэлементтерінің образдарының жиыны С жиынының образы деп аталады. Барлық вÎDÍr_Gэлементтерінің прообраздарының жиыны D жиынының прообразы деп аталады.

Анықтама. Егер анықталу облысынан (d_G) алынған кез-келген а элементінің мәндер жиынында (r_G) бір ғана образы bÎr_G болса, G – функционал (бір мәнді) сәйкестік деп аталады.

Анықтама. Егер G сәйкестігі толық анықталған,сюръективті, функционалды және " bÎr_G элемен тінің анықталу облысында бір ғана прообразы aÎd_G болса, онда G өзара бір мәнді сәйкестік болады.

Егер А мен В жиындарының арасында өзара бір мәнді сәйкестік болса, онда олардың қуаттары тең және олар тең қуатты жиындар |A|=|B| деп аталады.Бұл фактілер жиынды санамай-ақ,олардың тең қуаттылығын анықтауға болатындығын көрсетеді. Қуаты белгілі немесе оңай санауға болатын басқа жиынмен өзара бір мәнділігін дәлелдеу арқылы жиын элементтерін санамай-ақ оның қуатын анықтауға болады. N натурал сандар жиыны мен тең қуатты жиындар саналымды жиын деп аталады.

R нақты сандар жиынымен тең қуатты сандар континуальды деп аталады.

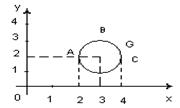
1- мысал. Айталық , G (x-3)²+(y-2)²≤1 қатынасын қанағат тандыратын барлық (х,у) нақты санды сандар жиыны болсын. G={(x,y)|x,yÎ үшін (x-3)²+(y-2)²≤1} сәйкестігінің графикалық кескіні центрі (3,2) нүктесінде болатын ,радиусы 1-ге тең дөңгелек. Бұл 3.2 суреттегідей G дөңгелегі R мен R арасындағы сәйкестік ( яғни ОХ өсі мен ОУ өстерінің арасындағы сәйкестік).

а) 2, 3, 4 сандарының образы мен прообраздарын табу керек.

Шешуі: 2Îd_G G сәйкестігіндегі образы жалғыз ғана 2Îr_G, 3-ң G сәйкестігіндегі образы [1,3] кесіндісіндегі барлық нақты сандар жиыны , 4-ң образы 2. G сәйкестігінің мәндер жиыны r_G алын ған (2Îr_G ) 2 санының G сәйкестігіндегі прообразы [2,4]Íd_G ; 3Îr_G G сәйкестігіндегі прообразы 3Îd_G. 4Îr_G – G сәйкестігінде прообраздары жоқ

б) 1) [2,3] Îd_G сандарының образы осы [2,4] кесіндідегі барлық образдарының бірігуі, яғни [1,3]Ìr_G;

2) Осыған ұқсас [2,4] кесіндісінің G сәйкестігіндегі образы [1,3];

3) [2,3] кесіндісінің прообразы [2,4] ; [2,4]Ìr_G прообразы [2,4];

Егер G сәйкестігі нақты сандар жиынында анықталған десек, яғни GÍRхR онда

1) G – толық анықталмаған себебі ,d_G¹R (d_GÌR)

2) Сюръективті емес себебі , r_G¹R (r_GÌR)

3) Функционалды (бір мәнді) емес, себебі [2,4]=d_G үшін (2 мен 4-тен басқа) образдар жалғыз емес.

4) Өзара бір мәнді болудың қажетті шарттары (1,2,3 шарттар) орындалмағандықтан сәйкестік өзара бір мәнді емес.

Егер сәйкестік G Í[2,4]х[1,3] болса G толық анықталған және сюръективті ,бірақ функционал ды және өзара бір мәнді емес.

2 мысал. Айталық G сәйкестігі x-2=y, x,y≥0 түзуінің бойындағы нүктелер жиыны

G={(x,y)|, x-2=y, x,y≥0}; G={ элементтері x-2=1 қатынасын қанағаттандыратын нүктелер жиыны}. G – сәйкестігінің қандай қасиеттері бар?

Шешуі: Егер G нақты сандар жиынында берілген сәйкестік (GÍRхR ) болса,онда:

1) G толық анықталмаған сәйкестік, себебі

d_G =[2,∞)ÌR;

2) Сюръективті емес, себебі анықталу облысы r_G =R₊=[0,∞] нөлмен қоса алғанда барлық нақты сандар жиыны.

3) Функционалды, себебі " xÎd_G, r_G – анықталу облысынан алынған

әрбір х-ке бір ғана yÎr_G сәйкес (х-ң бір ғана образы бар).4) Өзара бір мәнді емес, себебі толық анықталмаған және сюръективті емес.

2. G сәйкестігі нөлмен қоса алғандағы R ₊ жиынында яғни G Í R₊ ´ R₊ берілген болса, онда G сәйкестігінің төмендегідей қасиеттері болады:толық анықталмаған ,себебі dG = [2, ¥) және dG Ì R₊;

• сюръективті, себебі анықталу облысы rG = R₊;

• функциональды;

• Өзара бір мәнді емес, себебі толық анықталмаған .

3. G сәйкестігі G Í [2, ¥) х R+ болса :

• в толық анықталған;

• сюръективті;

• функциональды;

• Өзара бір мәнді ,себебі алдыңғы аталған қасиеттерге қоса, анықталу облысынан алынған кез –келген yÎrG үшін бір ғана прообраз бар.