Жиындардың өрнектелуі

Жиындарды өрнектеу үшін оған қандай элементтердің жататындығын көрсету керек. Оны бірнеше әдістермен жасауға болады.

1. Жиынға жататын элементтер тізімін көрсету арқылы. Тізіммен тек ақырлы жиындарды көрсетуге болады. Тізім фигуралы жақшамен қоршалады: M = {a₁, a₂,…, a_n}.

Мысалы, процессор a, монитор b, клавиатура c және принтерден d тұратын компьютер А жиынын былай өрнектеуге болады: A = {a, b, c, d}

2. Жиын элементтерінің (сипаттамалық предикат арқылы) немесе қандай да бір қасиетін көрсету арқылы. Айталық Р(х) А жиынының элементтері қанағаттандыратын я қанағаттандырмайтын қандай да бір қасиет болсын. Олай болса А жиынының Р қасиетін қанағаттандыратын барлық элементтерінен тұратын М жиыны M = { x | P(x)} немесе M = { x : P(x)} деп жазылады.

Ескерту: Сипаттамалық предикат Р(х) – логикалық тұжырым формасындағы шарт (немесе логикалық мән қайтаратын процедура). Егер жиын элементі үшін шарт орындалса элемент жиынға жатады, әйтпесе жатпайды. Мысалы, барлық натурал жұп сандар жиыны 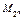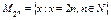болып, ал компъютердің сыртқы құрылғылар жиыны А = {х : х – PC сыртқы құрылғылар жиыны} болып өрнектеледі.

3. Туындатқыш процедура арқылы: M = {x | x : = f }.

Туындатқыш процедура дегеніміз – алдыңғы алынған элементтерден немесе обьектілерден жиын элементтерін алу әдісі болып табылады. Туындатқыш процедура іске қосылған кезде алынған объектілер жиынның элементі болып отырады. Мысалы, 2-ң дәрежесі болып табылатын барлық бүтін сандар жиынын 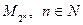, ( 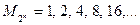) рекурсивті немесе индуктивті деп аталатын 2 түрлі тәртіппен алынатын туындатқыш процедура арқылы өрнектеуге болады

а) 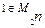; б) егер 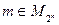болса, онда .

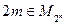Мысалдар:

1. Барлық натурал сандар жиынын әртүрлі әдістермен өрнектеңіз: 1, 2, 3,...

Шешуі: N натурал сандар жиыны шексіз болғандықтан оны тізім арқылы өрнектеуге болмайды.

Туындатқыш процедура екі ережеден тұрады:

a) 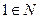; б) егер 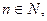онда .

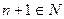N жиыны элементтнрінің қасиеттерін сипаттау арқылы: N = {х : х – бүтін оң сан}.

2. Айталық U = {a, b, c}. Айқын түрде (элементтерін тізбектеу арқылы) U жиынының элементтерінен тұратын барлық ішкі жиындардың жиыны b(U) булеанын анықтаңыз. b(U) жиынының қуаты қандай ?

Шешуі: b(U)={Æ, {а}, {b}, {с}, {а, b}, {а, с}, {b, с}, {а, b, с}}, |b(U)|=8.

Анықтама. Егер А жиынының барлық элементтері В жиынында жатса, онда А жиыны В жиынының ішкі жиыны деп аталады да,

А ÍВ деп белгіленеді, А жиыны В жиынына кіреді деп оқылады (А Ë В – А жиыны В-ның ішкі жиыны емес ). Бұдан шығатын тұжырым:

А Í В Û ∀ х ( x Î A Þ x Î B ), яғни кез келген х үшін, егер х Î А болса, онда х Î В.

Анықтама А мен В жиындары тең болады, егер А Í В және В Í А болса, яғни тең жиындар бірдей элементтерден құралады. (А Í В және В Í А) А, В жиындары бір бірінің ішкі жиыны. Мысалдар:

N Í Z, Z Í Q, Q Í R, R Í C дұрыс.

M₁ = {x | sin x = 1} және M₂ = {x | x = 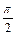+ 2kp, k Î Z} жиындарының тең екендігін ( M₁ = M₂) дәлелдеу керек болсын.

Шешуі. a) Егер х Î М₁ болса, онда х sin x = 1 теңдеуінің шешімі болғаны,яғни оны x = 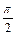+ 2kp, k Î Z деуге болады. Демек, жиынның анықтамасы бойынша х Î М₂. Олай болса М₁ Í М₂.

в) Егер х Î М₂ болса, х = 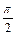+ 2kp, k Î Z деуге болады, яғни онда х мәні sin x = 1 теңдеуінің шешімі. Демек M₂ Í M₁ бұдан M₁ = M₂.

Анықтама. Егер А Í В және А ¹ В болса, онда А жиыны В-ға қатаң кіреді дейміз және А жиыны В-ның меншікті ішкі жиыны деп аталады. Анықтамаларға байланысты төмендегідей тұжырымдарды жазуға болады:

1. " X: Х Í Х; 2. " М: Æ Ì М; 3. Егер Х Í У, ал У Í Z, онда Х Í Z; 4. Х Í У, ал У Í Х, болса, онда Х = Ү;

Жиындардың теңдігін дәлелдеу үшін олардың бір-біріне ішкі жиын болатындығын көрсету керек.

Элементтің жиынға жатуы (Î) мен жиынның басқа жиынның ішкі жиын болуын (Í), яғни жиынның басқа жиынға кіруі ұғымдарын шатастырмау керек (Î, Í). О Î {о} және {o} = {{o}} болғанымен O Î {{o}} деу дұрыс емес, себебі {{o}} жиынының жалғыз ғана элементі {o} бар. (о – элементі бола алмайды).

Анықтама. Элементтердің ақырлы санынан тұратын жиын, ақырлы жиын деп аталады, керісінше болса ақырсыз жиын деп аталады. Мысалы N, R жиындары ақырсыз.

Анықтама. Ақырлы жиындардағы элементтердің саны жиынның қуаты деп аталады және | | белгілерімен қоршалып жазылады. Мысалы, М – ақырлы жиын болса, оның қуаты | M |. Қуаты 0-ге тең жиын, яғни элементтері жоқ жиын бос жиын деп аталады және Æ белгіленеді | Æ | = 0. (|{Æ}| = 1емес) Бос жиын кез-келген жиынның ішкі жиыны болады деп есептеледі.Егер А және В жиындары тең болса, олар тең қуатты жиындар деп аталады. Мысалдар:

1. А = {1, 2, 3}, B = {3, 4, 5}, A ¹ B.

2. A = {1 ,2 ,3, 4}; B = {4, 3, 1, 2}; A = B, себебі A Ì B, B Ì A;

3. A = {1, 2, 3}; B = {2, 4, 6}; C = {1, 2, 3, 4, 5}, A Ì C; B Ë A.

Анықтама. А жиынының барлық ішкі жиындарының жиынтығы булеан немесе дәрежелі жиын деп аталады және Р(А) деп белгілінеді (2^А деп те белгіленеді). Сонымен, 2^А = P(A) ⇆ {B | B Í A} немесе 2^А. Мысалдар: Егер А = {1, 2 ,3} болса, P(A) = {Æ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 2, 3}}.

Анықтама. Қарастыруға болатын барлық мүмкін элементтерден тұратын жиын универсал немесе универсум деп аталады және U деп белгіленеді.

1.3. Жиындармен операциялар (амалдар).

P(U) булеанындағы операцияларды және олардың геометриялық кескінделулерін қарастырамыз.

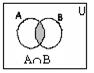
1. Қиылысу операциясы. Егер A,B Í P(U) онда, осы А, В жиындарының екеуіне де тиісті элементтерден тұратын жиынды А, В жиындарының қиылысуы деп атайды және ол төмендегідей өрнектеледі:

AÇB⇆{x | xÎA & xÎB}; Мысалы, A{1,2,3}, B{3,4,5} болса AÇB={3};

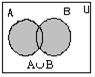2. Бірігу операциясы. А,В жиындарының ең болмаса біреуіне тиісті элемент терден тұратын жиынды А,В жиындарының бірігуі деп атайды және ол төмендегідей өрнектеледі:

A È B ⇆ {x | x Î A ∨ xÎB} Мысалы, A={1, 2, 3, 4};

B={4, 3, 6, 7} болса, AÈB = {1, 2, 3, 4, 6, 7}

А,В жиындарының қиылысуын олардың көбейтіндісі (А*В), ал бірігуін олардың қосындсы (А + В) деп те атайды

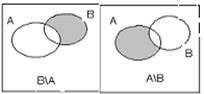
Жиындардың айырымы. А жиынының В-ға кірмейтін элементтерінен тұратын жиынды А,В жиындарының айырымы деп атаймыз және ол төмендегідей өрнектеледі:

А\В⇆A-B⇆{x|xÎA және хÏВ}.

A{1,2,3}, B{3,4,5} болса, A\B={1,2}; B\A ={4,5};

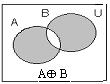
3. Сақиналы қосынды. А,В жиындарының өзара айырымдарының бірігуін сақиналы қосынды немесе симметриялық айырым деп атайды AÅB⇆(A\B)È(B\A) болып белгіленеді. (А\В)¹(В\А).Жоғарыда қарастырылған А,В үшін: A={1,2,3,4}; B={4,3,6,7} ; А \ B ={1,2,3,4} \ {3,4,6,7}={1,2}B\А=

{3, 4, 6, 7}\{1, 2, 3, 4} = {6, 7}; А Å В = {1, 2, 6, 7};

Симметриялық айырымның тағы бір формуласы:

AÅB=A¸B=AÅB ⇌(AÈB)\(AÇB);

AÅB={1, 2, 3, 4, 6, 7} \ {3, 4}={1, 2, 6, 7}.

4. Жиынының толықтауышы. U универсумындағы А-ға тиісті емес элементтер U универсумындағы А жиынының толықтауышы деп аталады (А-ны U-ға дейін толықтыратын) Ā⇆U\A болып белгіленеді.

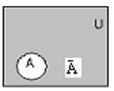
Мысалы, A = {1,2,3,4} жиынының толықтауышы. Ā ={6,7}; B={4,3,6,7} жиынының толықтауышы 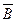={1,2} ; {Ç,È,-} операциялары буль операциялары деп аталады.

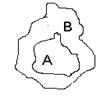
5. Анықтама. Жиындардың геометриялық кескіндері Эйлер-Венн диаграммалары деп аталады. Біріктіру, қиылысу операцияларын кез-келген жиындар дың жиыны болатын А_i (мұндағы і Î І жиынының элементтерін қабылдайды) жиынына да анықтауға болады:

Айталық І – элементтері индекс ретінде қолданылатын қандай да бір жиын болсын және " і Î І үшін А_і белгілі болсын. Олай болса, қиылысу 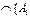| 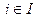} мен бірігуді 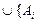| іÎ I} төмендегідей анықтауға болады. 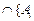| 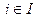}={x | x Î A _{і ,} " (кез-келген,барлық) іÎI үшін }; 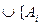| іÎ I} ={x | x Î A_і , 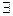(ең болмағанда бір і Î I үшін } теңдіктерімен беріледі. Көбінесе, 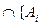| 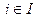}, 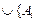| іÎ I} орнына 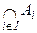, 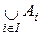немесе текстің мәтінінен І жиынының қандай екенді гі белгілі болса жай ғана 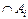, 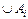белгілерін қолданады. 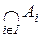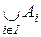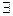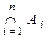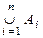={x|xÎA _{I ,} "іÎI}; ={x|xÎA_{I ,} іÎI}; Егер I={1,2,…,n}болса A₁ÇA₂ÇA₃Ç…ÇA_n ; A₁ÈA₂ÈA₃ È…ÈA_n ; және белгілеулері қолданылады.