Функциялар мен бейнелеулер
Айталық, А, В жиындарында f Í AхB сәйкестігі бар болсын. Анықтама Егер df=A, rf=B және 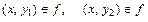 болғандығынан
болғандығынан 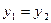 болса, онда
болса, онда 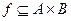 сәйкестігі функция деп аталады ол f : A®B немесе
сәйкестігі функция деп аталады ол f : A®B немесе 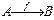 болып жазылады. Бұл анықтамадан функция дегеніміз функционал сәйкестік екендігін көреміз және f функциясының типі А®В деп оқылады. f функциясы анықталу облысының әрбір элементіне (х) мәндер облысынан бір мәнді (у)сәйкестендіреді және у = f (х)болып белгіленеді. ) (х аргумент, у функцияның мәні) болып жазылады (у х-тың образы).Мысалдар: f={(1,2),(2,3),(3,2)} – функция; f={(1,2),(1,3),(2,3)} - функция емес; {(x,x2-2x+3), xÎR} – функция ; бұл функция әдетте y=x2=2x+3 болып жазылады.
болып жазылады. Бұл анықтамадан функция дегеніміз функционал сәйкестік екендігін көреміз және f функциясының типі А®В деп оқылады. f функциясы анықталу облысының әрбір элементіне (х) мәндер облысынан бір мәнді (у)сәйкестендіреді және у = f (х)болып белгіленеді. ) (х аргумент, у функцияның мәні) болып жазылады (у х-тың образы).Мысалдар: f={(1,2),(2,3),(3,2)} – функция; f={(1,2),(1,3),(2,3)} - функция емес; {(x,x2-2x+3), xÎR} – функция ; бұл функция әдетте y=x2=2x+3 болып жазылады.
АнықтамаТолық анықталған функция f : A®B А-ны В-ға іштей бейнелеу деп аталады.
f : A 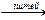 B ( df=A , r f ÍB) толық анықталған функция
B ( df=A , r f ÍB) толық анықталған функция
Анықтама Егер r f = B болса функция сюръективті функция деп аталады.
Анықтама Егер функция толық анықталған (rf=A) және сюръективті (rf=B) болса ,онда ол А-ны В-ға толық бейнелеу деп аталады: f : A  B болып жазылады.
B болып жазылады.
Анықтама .А 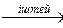 А бейнелеу А жиынын түрлендіру, ал А
А бейнелеу А жиынын түрлендіру, ал А  А бейнелеуі А-ға алмастыру деп аталады А
А бейнелеуі А-ға алмастыру деп аталады А 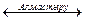 А болып та белгіленеді.
А болып та белгіленеді.
f және g функциялары тең болады, егер төмендегі шарттар орындалса:
• Олардың анықталу облыстары біреу -ол Ажиыны;
• Кез-келген а Î A үшін f(a) = g (a).
| Сәйкестік | Міндетті түрде болу керек қасиеті | ||
| Функционалды | Толық анықталған | Сюръективті | |
| Функция А-ны В-ға іштей бейнелеу А-ы В-ға толық бейнелеу | + + + | + + | + |
f: А1´А2´...´Аn ® Втипті функция п –орындыфункция деп аталады.Бұл жағдайда функцияның п аргументі бар деп түсіну келісілген.:f(а1,..., аn)=b, мұндағы а1ÎА1,...,аnÎАn, bÎВ. Айталық, GÍAхB сәйкестігі берілсін. Тек (а,b)ÎG болса ғана (b,a)ÎН болатын HÍBхA сәйкестігі, G-ң кері сәйкестігі деп аталады және G-1 болып белгіленеді.
Анықтама Егер f:A®B сәйкестігіне кері сәйкестік функционалды болса (яғни әрбір bÎrf үшін бір ғана aÎdf болса), онда ол f функциясына кері функция деп аталады, f -1 болып белгіленеді.
Кері сәйкестікте образ бен прообраздың орындары ауысып келетіндіктен f функциясына кері функция болу үшін f : A®B f функциясының мәндер жиынының әрбір bÎr f элементінің жалғыз ғана образы болу керек. Бұдан f : A®B функциясы өзінің анықталу облысы мен мәндер облысының өзара бір мәнді сәйкестігі болса ғана оған кері функция болатындығы көрінеді.
Егер h(x) = g(f(x)), мұндағы, хÎА орындалса h:А®С функциясы f және g функцияларының композициясы деп аталады және f(g) белгіленеді.
Көбіне h функциясы f ті g –ң орнына қойғаннан алынды деп айтады.Көп орынды f: Ат ® В, g: Вn® С функциясы үшін f-ті g –ға қоюдың әртүрлі варианттары бар. Нәтижесінде әртүрлі типтегі функциялар алынады. Мысалы, т = 3 және п = 4 үшін h = g (x1, f(у1,у2, у3), х3, х4) функциясында 6 аргумент бар ал оның типі В ´ А3 ´ В2 ® С. Аргументтерін басқаша атап f1,...,fn функцияларын бір-біріне қойғаннан алынған функция f1,...,fn функ-цияларының суперпозициясы деп аталады. Бұл суперпозицияны және функ-ционалдық белгі мен аргументтердің символдарын сипаттайтын өрнек формула деп аталады.
Функциялардың берілу тәсілдері:
• График түрінде;
• Кесте;
• Функцияны басқа функциялардың суперпозициясы түрінде сипаттайтын формула түрінде;
Анықтама. Егер f -1 сәйкестігі толық емес функция болса, яғни " x1, x2Îdf үшін, x1¹x2 болғандығынан f(x1)¹f(x2) болса, f функция инъективті (Инъекция) функция деп аталады..Егер f – инъекция болса f: 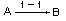 болып белгіленеді.
болып белгіленеді.
Анықтама. Егер rG = B болса f:A®B функциясы сюръективті (сюръекция) функция деп аталады f: 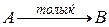 .
.
Анықтама. Егер f инъективті және сюръективті болса, ол биективті деп аталады: f:A«B
Анықтама. Егер f А-ы В-ң әр түрлі мәндеріне бейнелесе, онда f функциясы өзара бір мәнді сәйкестік немесе биективті функция (биекция) деп аталады. Сонымен, егер функция сюръективті және инъективті болса, функция биекция болады. Егер f А мен В арасындағы биекция болса, f : A«B болып жазылады. F: A«A биекциясы А жиынының (подстановка) алмастыруы деп аталады.
Суретте графиктік түрде функциялар берілген
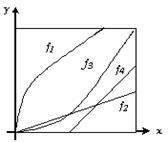
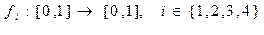
f1 – сюръективті, инъективті емес
f2 – инъективті, сюръективті емес
f3 – инъективті, сюръективті – биекция
f4 - инъективті де емес, сюръективті де емес
2- мысал: Үш функцияны қарастырайық 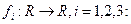
1) 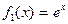 инъективті, сюръективті емес
инъективті, сюръективті емес
2) 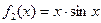 сюръективті, инъективті емес
сюръективті, инъективті емес
3) 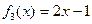 биективті;Негізгі әдебиет: 1[10-14]; 2[10-16]
биективті;Негізгі әдебиет: 1[10-14]; 2[10-16]
Қосымша әдебиет: 7[9-34]
Бақылау сұрақтары:
1. Сәйкестік,бейнелеу,функциональды бейнелеу дегеніміз не?
2. Қандай бейнелеулер инъективті, сюръективті, биективті деп аталады?
3. Кері функция бар болудың қажетті және жеткілікті шарты?
3-Дәріс. Жиындардың қуаты (2 сағат)
Дата добавления: 2015-08-14; просмотров: 5432;
