Дәріс конспектісі.

Берілген А және В ақырлы жиындарының қуаттарының теңдігін олардың элементтерін санау арқылы білуге болады. Мысалы, A={a, b, c, d, e, f}; B={α, β, γ, δ, ε, ζ}; |A| = |B| =6.

Жиындардың теңдігін білудің басқа да жолы бар:

Егер а ÎA үшін бір ғана bÎB сәйкес болса және керісінше әрбір bÎB үшін бір ғана aÎA сәйкес болса, онда А және В жиындарының арасында өзара бір мәнді сәйкестік бар дейді.Мұндай жиындар эквивалентті немесе тең қуатты жиындар деп аталады. Айталық N натурал сандар жиыны болсын 1, 2, 3, 4, 5, …, M – олардың квадраттарының жиыны: 1, 4, 9, 16, 25, Олай болса, N ~ M.

Натурал сандар жиынына эквивалентті жиындар саналымды жиындар деп аталынады. Саналымды жиын туралы мынадай теорема бар:

1-Теорема. Қандай да бір жиын саналымды болу үшін, оның элементтерін шексіз тізбек түрінде кескіндеу қажетті және жеткілікті.

2-Теорема. Саналымды жиынның кез-келген ішкі жиыны саналымды жиын.

3-Теорема. Ақырлы немесе саналымды жиындардың бірігуі-саналымды жиын.

Салдар. Рационал сандар жиыны саналымды жиын. Шынында да барлық оң рационал сандарды шексіз кесте түрінде өрнектеуге болады:

1/1, 1/2, 1/3, 1/4, 1/5, …

2/1, 2/2, 2/3, 2/4, 2/5, …

3/1, 3/2, 3/3, 3/4., 3/5, …

4/1, 4/2, 4/3, 4/4, 4/5, …

…………………………,

Бұл кестені сол жақ жоғарғы бұрыштан бастап диагональ бойымен айналуға болады. Бірақ барлық шексіз жиындар саналымды емес.

Кантор теоремасы. [0;1] кесіндісіндегі барлық нақты сандар жиыны саналымды емес. Теореманы кері жорып дәлелдейміз . Айталық бұл жиын саналымды болсын. Демек, бұл жиынның барлық элементтерін шексіз тізбек түрінде өрнектеуге болады.

Α₁ = 0,а₁₁а₁₂а₁₃а₁₄…

Α₂ = 0,а₂₁а₂₂а₂₃а₂₄…

Α3 = 0,а31а32а33а34…

………………………

Төмендегі тәртіппен В = b1b2b3b4…шексіз ондық бөлшек тізбегін b1 ≠ a11, b2 ≠ a22, b3 ≠ a33 және т.б. құрайық. Бұл бөлшек айтылған тізбекке енбейді, себебі тізбектің бірінші мүшесінен оның бірінші цифры өзгеше, екіншісінен екінші цифры өзгеше т.б. Ендеше [ 0;1] кесіндісінің барлық нақты сандар жиыны саналымды емес. Бұл жиынның қуаты континуум (С қуатты), ал С қуатты жиын континуальды жиын деп аталады.

Теорема. [a,b] кесіндісінің бардлық нақты сандар жиыны континуум қуатты.

Шынында да y=a+(b - a)x функциясы [ 0; 1] және [ a; b] кесіндісінің нүктелерінің арасында өзара бір мәнді сәйкестік орнатады, демек [ a; b] кесіндісіндегі нақты сандар жиынының қуаты [ 0; 1] кесіндісіндегі нақты сандар жиынының қуатындай.

Теорема. Континуум қуатты ақырлы немесе саналымды жиындардың жиыны – континуум қуатты жиын болып табылады.

1 Салдар. Барлық нақты сандар жиыны континуум қуатты.

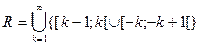
2 Салдар. Барлық иррационал сандар жиынының қуаты С. I=R/Q

Негізгі әдебиет: 2[12-20]; 3[10-43]

Қосымша әдебиет: 7[9-34]

Бақылау сұрақтары:

1. Қандай жиын саналымды жиын деп аталады?

2. Қандай жиындар континуум қуатты?

3. Ақырлы жиынға, континуум қуатты жиындарға мысал келтіріңіз.

4. Жазықтықтағы нүктелер жиынының қуаты қандай?

5. Екінің дәрежесі болатын сандардан құралған жиынның қуаты қандай?

4-Дәріс. Қатынастар. Бинарлы қатынастар. (2 сағ)

Дәріс конспектісі:

Қатынастар–жиын немесе жиындар элементтерінің арасындағы өзара байланыстарды беру тәсілдері. Қатынастардың ішінен унарлы, бинарлы қатынастар көбірек белгілі. Унарлы (бір орынды) қатынастар бір жиын элементтерінің белгілі бір R қасиетінің болуын бейнелейді.М жиынының R қасиетімен (белгісімен) ерекшеленетін элементтерінің жиыны М-ң бір ішкі жиынын құрайды.(Мысалы, қобдишадағы шарлардың бір бөлігінің ақ болуы) Оларды унарлы қатынас деп атайды, R мен белгіленеді, яғни aÎR, RÍM.

Бинарлы қатынастар.

Бинарлы қатынастар М жиынының бір жұп элементтерінің қандай да бір өзара қарым-қатынасын анықтауға қолданылады. Мысалы, М адамдар жиыны десек 2 адамның бір қалада тұруы, бір ұйымда қызмет істеуі, біреуінің екіншісінен жас болуы, әке мен бала болуы т. б.

Анықтама Екі орынды немесе бинарлы Р қатынасы деп А, В жиындарының декарт (тура) көбейтіндісінің (a,b) жұптарынан тұратын ішкі жиынын айтады және (a,b)ÎP, PÍA´B болып белгіле неді. А–Р қатынасының анықталу облысы, ал В мәндер облысы деп аталады.Айталық, PÍAxB қатынасы мына суреттегідей кескінделсін:

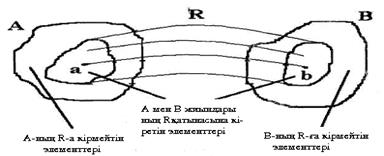
Бинарлы қатынас бір жиынның ішінде болса, мысалы М-жиынында болса Р қатынасы (a,b)ÎP, PÍMхM=M² немесе (a,b)ÎP, аРb болып белгіленеді. Жалпы жағдайда n орынды R қатынасы деп n жиынның тура (декарт) көбейтіндісінің R ішкі жиынын айтады:

R Í M₁ x M₂ x…x M_n

Егер (a₁,a₂,…,a_n)ÎR, ал (a₁ÎM₁,…,a_nÎM_n) онда a₁,a₂,…,a_n элементтері R қатынасында делінеді. Егер n орынды R қатынасы М жиынында болса, яғни M₁=M₂=…=M_n, онда RÍM ⁿ.