Бинарлық қатынастардың берілу тәсілдері.

Бинарлық қатынастар жиын болғандықтан, жиынның берілу тәсілдерінің бәрімен беріле алады. Ақырлы жиындарда берілген қатынастар әдетте төмендегідей әдістермен беріледі:

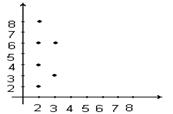
1. Бинарлы қатынас орындалатын жұптардың тізімі арқылы.Мысалы, A={2,3,4,5,6,7,8} жиыны берілсін. P={(x,y) | x,yÎA, y x-ке бөлінеді және x≤3} бинарлы қатынасын P={ (2,2), (2,4), (2,6) ,(2,8 ) ,(3,3) ,(3,6) } түрінде жазуға болады.

2. Графиктік түрде: Графиктік кескіндеудің бірнеше түрлері бар:

2.1. Координат өсьтеріне қатынастың элементтерін белгі леу арқылы. Алдыңғы мысалды графикалық түрде суреттегідей кескіндеуге болады.

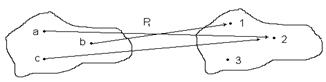
2.2. А мен В жиындарының элементтерінің арасындағы Р қатынасын стрелкалар арқылы көрсетуге болады.

Мысалы,A={a,b,c}; B={1,2,3} жиындары берілсін. Олардың элементтерінің арасындағы

P1={(a,2),(b,1),(c,2)} қатынасын төмендегі 6-суретпен кескіндеуге болады.

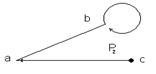
2.3. Граф арқылы да кескіндеуге болады. Мысалы, P₂={(a,b),(b,b),(c,a)} қатынасының граф түріндегі бейнесі 6-суреттегідей болады.

3. Бинарлы қатынастың матрица арқылы берілуі.A={a₁,a₂,…,a_n} және B={b₁,…,b_n} ақырлы жиындары және PÍAхB бинарлы қатынас берілсен. Р бинарлы қатынастың [P]=(P_ij) mхn мөлшерлі матрицасын төмендегі ережемен анықтаймыз:

P_{i j} =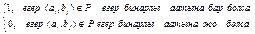

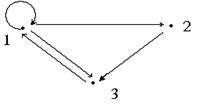
Алынған бұл матрица элементтер арасындағы байланыс туралы толық ақпарат береді және оны компьютерге өрнектеу мүмкіндігі бар. Мысалы, Суретте көрсетілгендей PÍA² A={1,2,3} бинарлы қатынасының матрицасы

[P]= 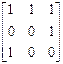; P={(1,1),(1,2),(1,3),(2,3),(3,1)}

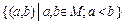2-мысал. M={1,2,3,4,5,6}. Егер Р < қатаң кіші болуды білдір се РÍМ х М қатынасын тізім және матрица түріндебейнелеу керек: Р қатынасы М жиынының a< b болатын элементтер жұбынан тұрады. Р= . Олай болса, Р қатынасын тізім және матрицамен беруге болады: Р={ (1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6)};

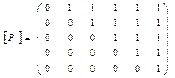Анықтама. Кез-келген жиын үшін анықталған Id_A={(x,x) | xÎA} қатынасы тепе-теңдік қатынас немесе диагональ қатынас деп аталады, ал U_A⇌A² универсалды немесе толық қатынас деп аталады. Айталық, Р – бинарлы қатынас болсын. d _P⇌{x | (x,y)ÎP қандай да бір Y үшін} жиыны Р қатынасының анықталу облысы деп, ал r_Р⇌{y | (x,y)ÎP қандай да бір Х үшін} жиыны Р қатынасының мәндер жиыны деп аталады. Мысалы, A = {2, 3, 4, 5, 6, 7, 8} жиынының P = {(x, y) | x, y Î A, у x ке бөлінеді және х ≤3} қатынасы үшін P={(2,2),(2,4),(2,6),(2,8),(3,3),(3,6)) қатынасы мен х={3} үшін анықталу облысы d_Р={2,3}. Мәндер аймағы r_Р={2,3,4,6,8};