Доказательство. С учетом отмеченного выше неравенства для функции каждое слагаемое можно оценить сверху следующим образом:

С учетом отмеченного выше неравенства для функции каждое слагаемое можно оценить сверху следующим образом:

После суммирования получим

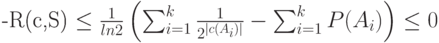
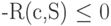причем последнее неравенство следует из неравенства Крафта (6.3) для префиксного кода и равенства . Таким образом, , что доказывает утверждение теоремы.

Из доказанной теоремы следует, что энтропия источника является нижней границей средней длины кодирования. Для источников, у которых вероятности являются целыми отрицательными степенями 2, эта граница достижима. Легко проверить, что для источника с распределением вероятностей 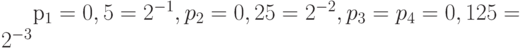средняя длина кодирования равна 1,75 и совпадает с энтропией источника.

Для доказательства второй теоремы потребуется функция , которая называется "потолок" и определяется выражением 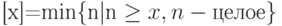. Необходимые для доказательства свойства этой функции легко следуют из ее графика, показанного на рис.6.7, и заключаются в выполнении неравенств .

Рис. 6.7.График функции [x]

Теорема. Для каждого источника 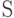найдется префиксный код , избыточность которого не превышает единицы, т. е. .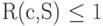

Пусть 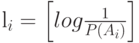, где функция "потолок". Тогда

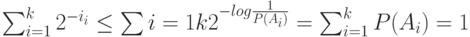
Это означает, что числа 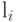удовлетворяют неравенству Крафта. Тогда из теоремы Крафта следует, что найдется префиксное кодирование , такое что 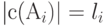. Оценим избыточность этого кодирования

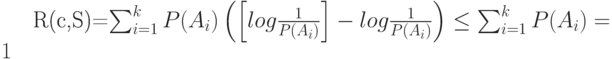
Теорема доказана.

Данная теорема гарантирует, что для любого источника найдется префиксный код со средней длиной кодирования, превышающейэнтропию не более чем на 1.