Избыточность кодирования. Нижняя граница средней длины кодирования

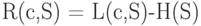Рассмотренные ранее примеры показывают, что использование кодов переменной длины позволяет эффективнее кодировать сообщения по сравнению с равномерным кодированием. Для получения оценки минимально достижимой средней длины кодового слова рассмотрим избыточность кодирования , представляющую собой разность между средней длиной кодового слова при кодировании источника S кодом c и энтропией. Две следующие теоремы показывают, какова нижняя граница средней длины кодирования и как близко можно приблизиться к этой границе за счет рационального выбора кодовых слов.

Для доказательства первой теоремы напомним одно свойство логарифма, которое заключается в том, что график функции лежит ниже касательной к ней в точке 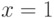, и следовательно, выполняется неравенство 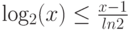. Это свойство иллюстрирует рис.6.6.

Теорема. Для произвольного источника 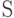и префиксного кода избыточность кодирования неотрицательна, т. е. .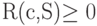

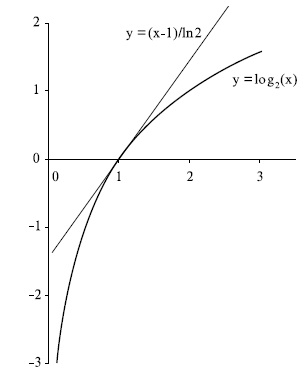
Рис. 6.6.График функции log2(x) и касательной к ней в точке x=1