Теорема Гаусса-Остроградского

Вернемся к выражению для элементарного потока ∆N. Пусть электрическое поле создается точечным зарядом q; тогда модуль Е будет

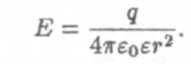
Элементарный поток в этом случае:

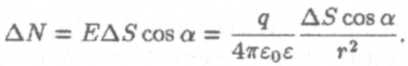
Площадь площадки соответствующего элементарного сегмента будет: ∆S₀ = ∆S cosа. Заметим, эта площадка площадью ∆S₀ перпендикулярна радиусу. Тогда по определению телесного угла можно написать:

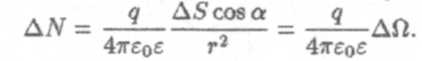
Полный поток вектора Ечерез произвольную замкнутую поверх­ность будет:

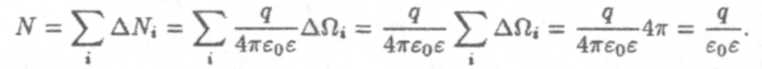
Таким образом, если точечный заряд расположен внутри произ­вольной замкнутой поверхности, то полный поток вектора напря­женности через эту поверхность равен:

Обратите внимание, что этот результат не зависит ни от фор­мы поверхности, ни от того, где внутри поверхности расположен заряд.

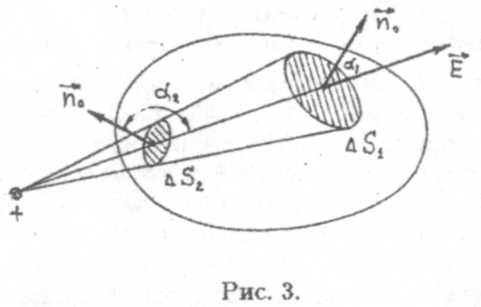
В случае, когда заряд находится вне замкнутой поверхно­сти, поток вектора напряженности от этого источника равен ну­лю. Это следствие пояснено на рисунке, на котором изображе­на эта ситуация: заряд находится вне замкнутой поверхности и следствием этого является тот факт, что полный поток ∆N в эле­ментарном телесном угле ∆Ω будет равен нулю из-за того, что угол, образованный вектором Еи вектором внешней нормали к поверхности n₀будет таким, что cosa₁> 0, а cosa₂ < 0 (рис. 3.)

Если внутри поверхности расположен не один точечный за­ряд, а их совокупность или заряд распределен на некоторой по­верхности или в некотором объеме, то формула (1) обобщается на основе принципа суперпозиции:

Теорема Гаусса-Остроградского:

Поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сум­ме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную и диэлектрическую проницаемость данной среды (2).

Используя теорему Гаусса, можно вычислить напряженность электрического поля вокруг заряженного тела при условии нали­чия симметрии относительно центра, плоскости или оси.