Напряженность поля равномерно заряженной бесконечной плоскости

Если плоскость бесконечна и заряжена равномерно, т.е. по­верхностная плотность заряда σ = q/S одинакова в любом ее месте (q — электрический заряд поверхности, S — площадь за­ряженной поверхности), то линии Ев любой точке перпендику­лярны плоскости. Очевидно, что такое же направление они со­храняют на любом расстоянии от плоскости и будут одинаковы по модулю, а это означает, что электрическое поле равномерно заряженной бесконечной плоскости будет однородным.

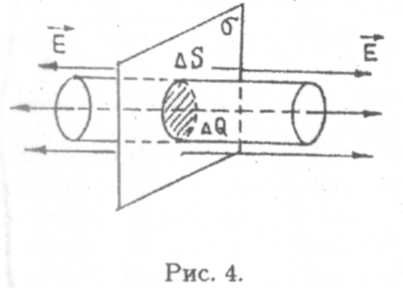
Выберем замкнутую цилиндрическую поверхность, основа­ния которой площадью ∆S параллельны плоскости и показаны на рис. 4.

Вектор Епараллелен оси цилиндра и перпендикулярен его основаниям (рис. 4). По теореме Гаусса:

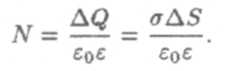
По определению потока вектора: ∆N = 2E∆S(поток вектора через боковую поверхность цилиндра равен нулю). Из двух вы­ражений получаем:

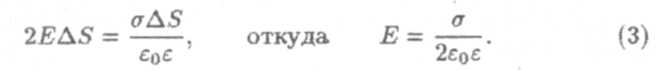
Формула (3) определяет напряженность поля равномерно заря­женной бесконечной плоскости.