Теплоемкость газа. Теплоемкостью тела СТ называют отношение количества теплоты Q, сообщенного телу, к изменению температуры ∆T

Теплоемкостью тела С_Т называют отношение количества теплоты Q, сообщенного телу, к изменению температуры ∆T, вызванному этой теплопередачей.

Различают удельную теплоемкость вещества (с) и молярную те­плоемкость (С).

Удельной теплоемкостью вещества называют количество теплоты, необходимое для нагревания 1 кг вещества на 1 К

Молярной теплоемкостью называют количество теплоты, необходимое для нагревания 1 моля вещества на 1К.

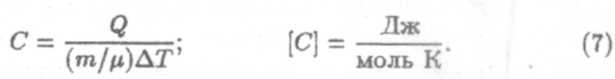
Между удельной и молярной теплоемкостями существует оче­видная связь

Далее для простоты все рассуждения и формулы будут связаны с молярной теплоемкостью.

Оказывается, что теплоемкость существенно зависит от того, при каких условиях нагревается газ. Различают теплоемкость при постоянном объеме С_vи теплоемкость при постоянном да­влении С_р. При постоянной температуре теплоемкость равна бесконечности, так как ∆T= 0.

Рассмотрим 1 моль газа, нагреваемый при постоянном объ­еме (V = const, v = т/μ = 1 моль). На основании первого начала термодинамики все поступающее газу тепло идет на из­менение его внутренней энергии Q = ∆U.

Получим выражение для теплоемкости газа при постоянном объеме.

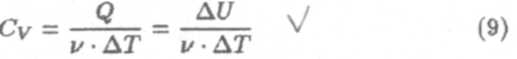
Учитывая, что ∆U = (i/2)v/R∆T, получим:

Таким образом, молярная теплоемкость при постоянном объеме зависит только от числа степеней свободы i молекулы газа, т.е. от количества атомов в молекуле и от ее структуры.

Теперь пусть 1 моль газа нагревается при постоянном да­влении (р = const, v = 1 моль). В этом случае поступающее газу тепло идет, в соответствии с первым началом термодина­мики, не только на изменение его внутренней энергии, но и на работу расширения газа (именно расширение газа обеспечива­ет постоянство давления). А это означает, что теплоемкость газа при постоянном давлении больше его теплоемкости при по­стоянном объеме (С_р > С_v). Чтобы найти их разницу, вычи­слим предварительно работу расширения 1 моля газа при изо­барном процессе. В соответствии с формулой (3), эта работа А = р∆V = р(V₂ – V₁) = pV₃ – pV₁. Учтем уравнение Менделеева-Клапейрона, тогда

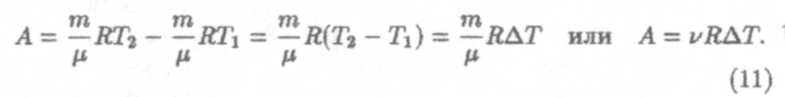
Формула (11) позволяет установить физический смысл универ­сальной газовой постоянной R. По условию р = const и v = 1 моль; положим, что ∆Т = 1К, тогда численно А = R или уни­версальная газовая постоянная численно равна работе расшире­ния одного моля идеального газа при нагревании его на 1К при постоянном давлении.

Чтобы найти формулу теплоемкости газа при постоянном давлении, воспользуемся определением молярной теплоемкости (7) и первым началом термодинамики

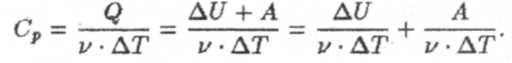
Учитывая в первом слагаемом формулу (9), а во втором (11), получим

Это выражение называется уравнением Майера.Подставим в это уравнение выражение (10), получим

Важной термодинамической характеристикой является отноше­ние теплоемкости при постоянном давлении к теплоемкости при постоянном объеме τ

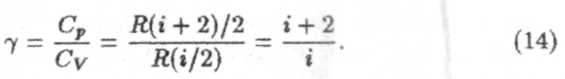
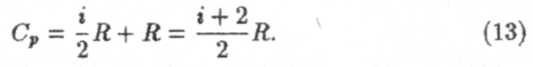
Из формул (10) и (13) следует, что по значениям теплоемкостей все газы можно подразделить на три сорта: одноатомные, двухатомные и многоатомные газы. Поэтому легко подсчитать все возможные значения их теплоемкостей. Все результаты и выводы из данного параграфа можно отнести к классической теории теплоемкостей. Непосредственные измерения показали, что справедлива эта теория в полном объеме только для одно­атомных газов. Двух- и многоатомные газы дают существенные отличия экспериментальных значений теплоемкости от теоре­тических, особенно при температурах, существенно отличаю­щихся от нормальной. Наиболее полно и правильно этот во­прос рассматривает квантовая теория теплоемкости. Выраже­ния для теплоемкости твердых тел можно найти в лекции №17.