Понятие импульса
Массой материальной точки называется скалярная физическая величина, описывающая инертные свойства тела при поступательном движении
Импульсом материальной точки называется векторная физическая величина р. равная произведению массы материальной точки т на ее скорость v. Импульс определяется по формуле:
p=mv (1)
Второй закон Ньютона
Быстрота изменения импульса материальной точки с течением времени равна действующей на нее силе:
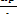 = F (2)
= F (2)
Второй закон Ньютона, записанный в форме (2), является релятивистски инвариантным, т.е. он применим как при малых
(t 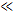 с), так и при больших (v
с), так и при больших (v 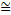 с) скоростях движения тела. Здесь с ~ 3,00 • 108м/с — универсальная мировая постоянная — скорость распространения света в вакууме. Как считается в современной физике, сигнал, информация или энергия не могут передаваться в пространстве со скоростью большей, чем с.
с) скоростях движения тела. Здесь с ~ 3,00 • 108м/с — универсальная мировая постоянная — скорость распространения света в вакууме. Как считается в современной физике, сигнал, информация или энергия не могут передаваться в пространстве со скоростью большей, чем с.
Если скорость тела мала (v 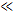 с) и масса тела постоянна (m = const), то второй закон Ньютона можно перпеписать в классической форме
с) и масса тела постоянна (m = const), то второй закон Ньютона можно перпеписать в классической форме
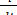 =
= 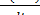 = m
= m 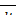 = ma = F (3)
= ma = F (3)
Отсюда следует, что
a=  (4)
(4)
т.е. ускорение материальной точки прямо пропорционально действующей на нее силе и обратно пропорционально массе материальной точки.
При больших (околосветовых) скоростях движения частиц в ускорителе необходимо использовать для расчета параметров движения только формулу (2), но никак не формулу (4). Второй закон Ньютона строго выполняется только в инерциальных системах отсчета.
Третий закон Ньютона
Силы взаимодействия между двумя материальными точками равны по величине, противоположны по направлению и направлены вдоль прямой, соединяющей emu точки.
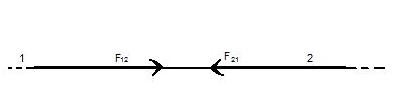
Рис. 1
Проиллюстрируем сказанное с помощью рис. 1. Используя обозначения, указанные на рисунке, аналитически третий закон Ньютона можно записать в форме:
F12 = - F21 (5)
Заметим, что силы, действующие по третьему закону Ньютона, не могут уравновесить друг друга, так как они приложены к разным материальным точкам. Строго третий закон Ньютона выполняется только при непосредственном контакте тел или отсутствии их взаимного перемещения. В системе СИ сила измеряется в ньютонах. [F] = Н = кг - м/с2. Все единицы системы СИ, образованные от фамилий, в сокращенном обозначении пишутся с большой буквы.
Закон изменения импульса
Воспользовавшись формулой (2), имеем
dp = Fdt. (6)
Следовательно,
изменение импульса тела dp за промежуток времени dt равно импульсу действующей силы Fdt.
Импульсом силы называется произведение силы на промежуток времени ее действия.
Если нам нужно найти изменение импульса тела за конечный промежуток времени [t1, t2], то интегрируя (6), найдем
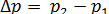 =
= 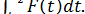 (7)
(7)
Формула (7) дает изменение импульса тела в случае действия переменной силы.
Закон сохранения импульса
Полагая в (2) F = 0, получим
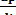 = 0, р= const. (8)
= 0, р= const. (8)
Это означает, что при отсутствии действующей силы импульс материальной точки есть величина постоянная.
Если имеется система материальных точек, то закон сохранения импульса можно сформулировать следующим образом.
Импульс замкнутой системы материальных тел есть величина постоянная.
Напомним, что замкнутой называется система материаль-
ных тел, внешним воздействием на которую можно пренебречь.
Для замкнутой системы, состоящей из п материальных тел, име-
ем:
P = p1 + p2 +…+ pn = const. (9)
Или
m1v1 +m2v2 +…+ mnvn = const. (10)
Приведем примеры применения закона сохранения импульса.
Пример 1. Абсолютно неупругий удар двух тел.
Абсолютно неупругим называется такой удар тел, в результате которого они движутся с одинаковой скоростью. Тогда имеем: импульс до удара р = m1v1 +m2v2, равен импульсу после удара р = m1v' + m2v', следовательно:
m1v1 +m2v2 = ( m1 +m2 ) v’, v’ =  . (11)
. (11)
Здесь v' скорость тел после удара. Заметим, что закон сохранения импульса позволяет, не вникая в детали того, как происходит удар, как тормозятся и ускоряются тела в процессе удара, сразу найти конечную скорость, т.е. заметно упростить решение задачи. В этом и заключается его сила.
Вообще законы сохранения дают нам инварианты, сохраняющиеся в Природе. Применение этих законов позволяет существенно упростить решение многих физических задач. В процессе развития физики велся поиск все новых и новых законов сохранения. Этот поиск продолжается до сих пор. Параллельно с ним происходит формирование новых физических понятий. Так в свое время были сформулированы законы сохранения: энергии, момента импульса, электрического заряда, барионного заряда, изотопического спина и другие. .
Пример 2. Абсолютно упругий удар двух тел.
Это удар, при котором сохраняется механическая анергия тел. Рассуждая аналогично тому, как это было сделано в "Примере 1", получим
m1v1 +m2v2 = m1v’1 + m2v’2 . (12)
Здесь v’1 и v’2 — скорости тел после удара.
Пример 3. Движение ракеты в безвоздушном пространстве.
Пусть покоящаяся ракета массой го выбросила со скоростью и порцию гада массой \dm\, в результате чего приобрела скорость dv. Составим уравнение сохранения импульса
(m + dm)dv = - udm (13)
Здесь учтено, что величина изменения массы ракеты dm — отрицательна. Уравнение (13) выражает тот факт, что импульс, полученный ракетой, равен по величине импульсу газов, но противоположен ему по знаку. Раскрывая в (13) скобки и пренебрегая бесконечно малыми второго порядка, найдем
dmv = - udm (14)
Поделив обе части (14) на m и интегрируя, получим
 = u
= u 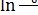 (15)
(15)
Или
v = uln 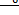 , m =
, m = 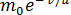 . (16)
. (16)
Здесь 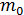 — начальная масса ракеты вместе с топливом, m — масса в данный момент времени, когда скорость ракеты достигла величины v.
— начальная масса ракеты вместе с топливом, m — масса в данный момент времени, когда скорость ракеты достигла величины v.
Для современных ракет скорость истечения газовой струи и ~ 4км/с. Формула (16) показывает, что для достижения ближайшей к Солнечной системе звезды Альфа Центавра (расстояние порядка четырех световых лет или 3,6 • 1013 км) и возвращения назад за время, равное человеческой жизни, потребуется начальная масса ракеты, в огромное количество раз превосходящая массу всей нашей Галактики.
Поэтому ракеты и космические корабли современого типа не позволяют решать проблему межзвездных перелетов. Для решения этой проблемы понадобятся новые идеи и другие конструкции космических кораблей. Подобные идеи уже есть. Формула (16) была получена русским ученым К.Э.Циолковским в 1903 году.
Реактивное движение
Под реактивным движением в узком смысле понимается движение ракет и реактивных снарядов. Под реактивным движением в широком смысле понимается движение тела за счет реакции струи жидкости или газа. В широком смысле винтовой самолет или морской корабль так же движутся реактивным образом. Вообще, если приглядеться повнимательнее к окружающему миру, то мы заметим, что многие виды движения совершаются на основе закона сохранения импульса, например, полет птиц, ползание червей и другие.
Подводя итог, отметим, что законы Ньютона являются, пожалуй, самыми важными законами механики, а вытекающий из них закон сохранения импульса есть один из самых фундаментальных законов Природы.
Лекция №3
Разновидности сил, играющих важную роль в механических процессах
Классификация фундаментальных взаимодействий, известных современной физике
В повседневном опыте мы встречаемся с разнообразными силами. Однако, несмотря на разнообразные названия, которые мы даем различным силам, существуют лишь два вида сил, управляющих движением тел в повседневной жизни — гравитационные и электромагнитные силы (или взаимодействия). Однако данных взаимодействий недостаточно для описания ядерных явлений. Исследование процессов с участием ядер и элементарных частиц показало, что в природе существуют еще два взаимодействия: сильные (ядерные) и слабые.
Гравитационные и электромагнитные взаимодействия являются дальнодействующими (т.е. их действие заметно на больших расстояниях). По этой причине именно они и ответственны за все крупномасштабные макроскопические явления, начиная от явлений повседневной жизни и кончая происходящими в далеких звездах и галактиках. В данной лекции кратко рассмотрим некоторые силы.
Сила трения
Сила трения препятствует скольжению соприкасающихся тел друг относительно друга, направлена по касательной к поверхности соприкасающихся тел и противоположна скорости движения данного тела (рис. 1).
Трение существует и в случае неподвижных тел — трение покоя. Если Fдв < Fтр ск, то v = 0. Если Fдв = Fтр ск, то a = 0, v = const и тело движется равномерно или покоится. Если Fдв > Fтр ск, то тело движется с ускорением.
Трение обусловлено шероховатостью поверхностей тел — взаимодействием этих поверхностей. При очень гладких поверхностях главной причиной трения становятся межмолекулярные силы сцепления.
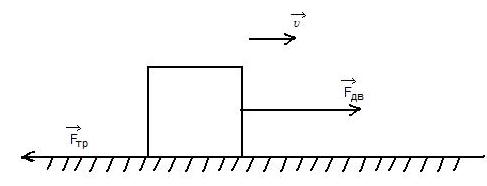
Рис. 1.
Опыт показывает, что приблизительно Fтр ск пропорциональна силе нормального давления N, т.е. силе, прижимающей тела друг к другу
Fтр ск = 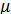 N (1)
N (1)
В случае скольжения тела по горизонтальной поверхности N = тg, а 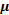 — коэффициент трения. Он зависит от многих причин: материала и качества обработки поверхностей, скорости движения, влажности, температуры и т.д. Коэффициент трения величина безразмерная и дается в таблицах. В сельскохозяйственной практике на различии
— коэффициент трения. Он зависит от многих причин: материала и качества обработки поверхностей, скорости движения, влажности, температуры и т.д. Коэффициент трения величина безразмерная и дается в таблицах. В сельскохозяйственной практике на различии 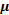 основано разделение семян растений. Например, для проса и овса
основано разделение семян растений. Например, для проса и овса 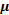 ов >
ов > 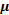 пр.
пр.
Подбором утла наклона транспортера а добиваются того, чтобы семена проса и овса (рис. 2) ссыпались с разных сторон ленточного транспортера. Там, где трение вредно, его уменьшают, применяя смазку (т.е. заменяя сухое трение жидким — внутренним трением). Другой способ — трение качения (катки, подшипники, колеса). 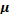 тр.кач
тр.кач 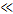
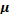 тр.ск. Сила трения качения обратно пропорциональна радиусу колеса
тр.ск. Сила трения качения обратно пропорциональна радиусу колеса
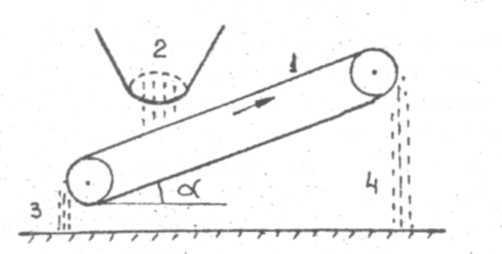
| 1 — лент» транспортера, 2 — бункер со смесью, J — просо, 4 — овес. Рис. 2. |
Fтр. кач. = 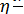 (2)
(2)
Коэффициент 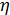 измеряется в метрах. По этой причине колеса телег иногда имеют большой радиус.
измеряется в метрах. По этой причине колеса телег иногда имеют большой радиус.
Сила упругости
С помощью внешней силы (Fдеф) тело можно деформировать, т.е. изменить форму и размеры тела. При этом в нем возникает противодействующая сила — сила упругости
Fдеф = - Fynp.
Рассмотрим, например, деформацию одностороннего растяжения. Она характеризуется величиной деформации (удлинением)  х (рис. 3).
х (рис. 3).
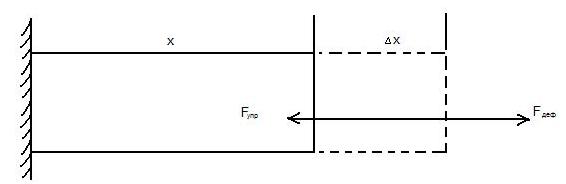
Рис. 3.
При устранении деформирующей силы сила упругости восстанавливает первоначальную форму и размеры тела (ликвидирует деформацию  х).
х).
Существует несколько видов деформации: одностороннее растяжение, односторонее сжатие, всестороннее растяжение, всестороннее сжатие, кручение, сдвиг, изгиб. Каждый вид деформации вызывает соответствующую силу упругости.
Закон Гука
Опыт показывает, что при малой деформации сила упругости пропорциональна величине деформации — закон Гука:
Fynp = -k  x, (3)
x, (3)
где к — коэффициент упругости (жесткости) измеряется в Н/м и зависит как от материала тела, так и от его размеров. Знак минус указывает на противоположность направлений Fynp и  х. Деформация называется упругой, если после устранения деформирующей силы тело полностью восстанавливает первоначальный размер и форму. Упругие деформации — малые деформации. При деформации в теле возникает внутреннее напряжение, равное отношению деформирующей силы F к площади поперечного сечения S деформируемого тела, оно измеряется в Паскалях (Па).
х. Деформация называется упругой, если после устранения деформирующей силы тело полностью восстанавливает первоначальный размер и форму. Упругие деформации — малые деформации. При деформации в теле возникает внутреннее напряжение, равное отношению деформирующей силы F к площади поперечного сечения S деформируемого тела, оно измеряется в Паскалях (Па).
При больших деформациях возникает остаточная деформация, при этом тело не восстанавливает полностью свою форму и размеры. При еще большей деформации тело разрушается. Остаточная деформация наступает, когда значение внутреннего напряжения превышает предел упругости.
Пределом упругости называют максимальное значение внутреннего напряжения, при котором еще имеет место упругая деформация.
Рассмотрим подробнее деформацию одностороннего растяжения. Опыт показывает, что
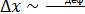 или
или 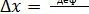 ,
,
где е — модуль Юнга, характеризующий упругие свойства вещества стержня и называемый модулем упругости.
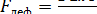 и
и 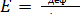 .
.
При S = 1 м2;  х = х будет Fдеф = Е, т.е. модуль Юнга численно равен силе, растягивающей стержень единичного поперечного сечения вдвое.
х = х будет Fдеф = Е, т.е. модуль Юнга численно равен силе, растягивающей стержень единичного поперечного сечения вдвое.
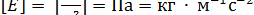 .
.
Модуль Юнга зависит от материала образца и дается в таблицах. Величина модуля Юнга колеблется от 0,17 • 1011 Па для свинца до 2,2 • 1011 Па для стали.
Все изложенное для одностороннего растяжения относится и к остальным видам деформации.
Дата добавления: 2015-08-11; просмотров: 1317;
